Solución Taller 2 - Inicio
Anuncio
UNIVERSIDAD DE LOS ANDES
FACULTAD DE ECONOMIA
TEORIA DE JUEGOS
Profesora: Marcela Eslava
Solución Taller 2
Fecha de Entrega: lunes 23 de febrero
1.a)
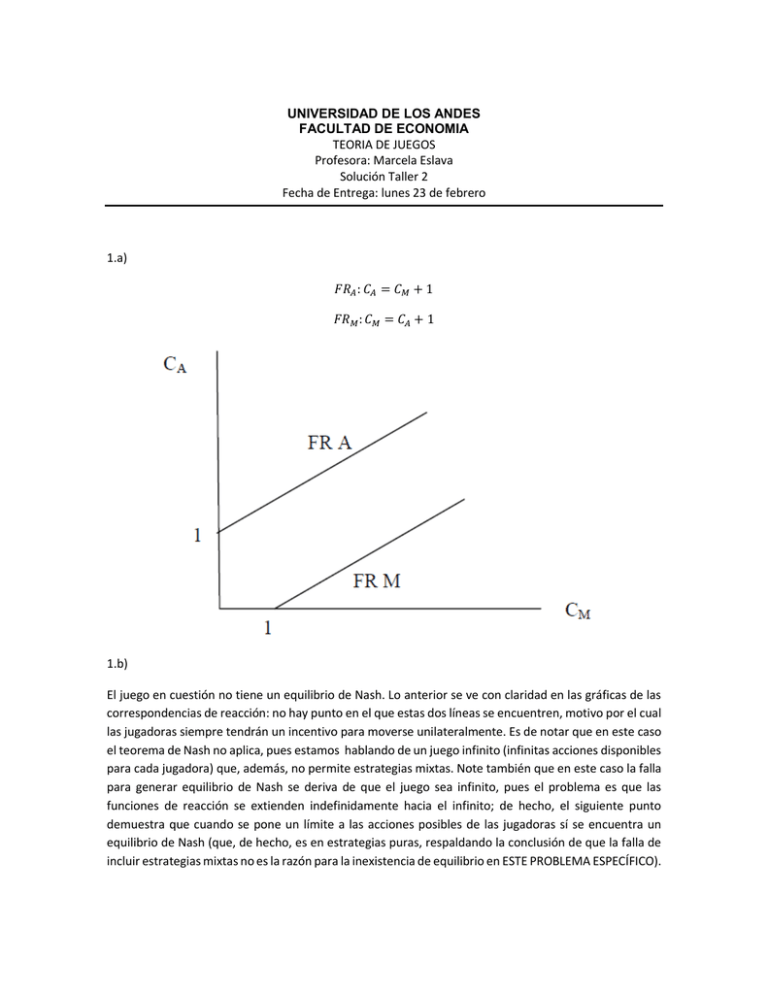
𝐹𝑅𝐴 : 𝐶𝐴 = 𝐶𝑀 + 1
𝐹𝑅𝑀 : 𝐶𝑀 = 𝐶𝐴 + 1
1.b)
El juego en cuestión no tiene un equilibrio de Nash. Lo anterior se ve con claridad en las gráficas de las
correspondencias de reacción: no hay punto en el que estas dos líneas se encuentren, motivo por el cual
las jugadoras siempre tendrán un incentivo para moverse unilateralmente. Es de notar que en este caso
el teorema de Nash no aplica, pues estamos hablando de un juego infinito (infinitas acciones disponibles
para cada jugadora) que, además, no permite estrategias mixtas. Note también que en este caso la falla
para generar equilibrio de Nash se deriva de que el juego sea infinito, pues el problema es que las
funciones de reacción se extienden indefinidamente hacia el infinito; de hecho, el siguiente punto
demuestra que cuando se pone un límite a las acciones posibles de las jugadoras sí se encuentra un
equilibrio de Nash (que, de hecho, es en estrategias puras, respaldando la conclusión de que la falla de
incluir estrategias mixtas no es la razón para la inexistencia de equilibrio en ESTE PROBLEMA ESPECÍFICO).
1.c)
1.d)
Hay al menos dos formas de proceder en este punto:
1. Encontrar todos los posibles equilibrios en estrategias mixtas permitiendo probabilidades
genéricas de que cada jugador juegue cada estrategia. . Los equilibrios de estrategias puras
serán aquellos en los que las probabilidades q y p adopten el valor de 0 y/o 1. Por ejemplo, si
p es la probabilidad con la que Andrea juega 1 y q aquella con la que Margarita juega 1, la
función de utilidad esperada de Andrea sería (luego de algunos pasos):
𝐸(𝑈𝐴 )= pq – 1.5p -0.5q
Que es decreciente en p para cualquier q en el rango posible (note que la derivada de esta
función con respecto a p es q-1.5, que es negativa si q cae en el rango [0,1]. Es decir, el p
óptimo es 0. Procediendo de manera similar, el q óptimo para Margarita es también 0. Es
decir, el único equilibrio es que ambas escojan una cantidad de 2.
2. Note, sin embargo, que para cada jugadora i la estrategia Ci= 2 domina estrictamente a la
estrategia Ci=1. Es decir, sin importar qué estrategia (pura o mixta) juegue la otra jugadora, i
no será indiferente entre Ci=1 y Ci=2. En estas circunstancias, jamás escogerá una estrategia
mixta entre Ci=1 y Ci=2, sino que preferirá la estrategia pura Ci=2.
Por tanto,
𝐸𝑁 = {𝐶𝐴 = 𝐶𝑀 = 2}
1.e)
Este juego no tiene equilibrio de Nash en estrategias mixtas (“estrictamente” mixtas). La razón es que
hay una estrategia de cada jugador que domina estrictamente a otra. Más en general (es decir, más allá
de este juego específico) como un jugador en equilibrio sólo escoge una estrategia mixta si es indiferente
entre las estrategias puras que está mezclando, y como una estrategia que domina a las demás para un
jugador será siempre estrictamente preferida a las demás por él, no se dará indiferencia y no habrá
equilibrios en que ese jugador juegue estrategias mixtas.
2.a)
Revisando las mejores respuestas de cada en la matriz de pagos, podemos encontrar lo siguiente:
De esta forma llegaríamos a los siguientes dos Equilibrios de Nash:
𝐸𝑁 = {(𝑆𝐺 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑎𝑟, 𝑆𝐶 = 𝑅𝑒𝑛𝑒𝑔𝑜𝑐𝑖𝑎𝑟), (𝑆𝐺 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑎𝑟, 𝑆𝐶 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑎𝑟)}
2.b)
Iniciamos notando que para los Campesinos 𝑆𝐶 = 𝑅𝑒𝑛𝑒𝑔𝑜𝑐𝑖𝑎𝑟 domina estrictamente a 𝑆𝐶 = 𝐴𝑝𝑜𝑦𝑜,
ya que ∀𝑆𝐺 , 𝑈𝐶 (𝑆𝐺 , 𝑅𝑒𝑛𝑒𝑔𝑜𝑐𝑖𝑎𝑟) > 𝑈𝐶 (𝑆𝐺 , 𝐴𝑝𝑜𝑦𝑜).
Tomando la matriz reducida, y procediendo con el mismo método de eliminación de estrategias
estrictamente dominadas, notamos que para el Gobierno 𝑆𝐶 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑎𝑟 domina estrictamente tanto
a 𝑆𝐺 = 𝐴𝑝𝑜𝑦𝑜 como a 𝑆𝐺 = 𝑅𝑒𝑛𝑒𝑔𝑜𝑐𝑖𝑎𝑟. Por tanto podemos realizar las siguientes eliminaciones:
Así, quedamos con la siguiente matriz reducida:
Note que la matriz reducida se limita a los Equilibrios de Nash hallados en el numeral anterior. De
proseguir con un proceso de eliminación iterativa de estrategias débilmente dominadas, llegaríamos a
una solución única, pero estaríamos eliminado uno de los equilibrios de Nash. Así, tanto
(𝑆𝐺 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑎𝑟, 𝑆𝐶 = 𝑅𝑒𝑛𝑒𝑔𝑜𝑐𝑖𝑎𝑟)
Como
(𝑆𝐺 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑎𝑟, 𝑆𝐶 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑎𝑟)
podrían ser soluciones resultantes de la eliminación iterativa de estrategias débilmente dominadas.
También es importante resaltar que, a diferencia del proceso de eliminación iterativa de estrategias
estrictamente dominadas, el orden de las eliminaciones sí importa (i.e., sí altera el resultado final)
cuando se sigue un proceso de eliminación débil.
2.c)
Observando el resultado tras el proceso de eliminación iterativa de estrategias estrictamente dominadas
(la primera parte del proceso explicado en el anterior numeral), notamos que el Gobierno elegiría tanto
𝑆𝐺 = 𝑅𝑒𝑛𝑒𝑔𝑜𝑐𝑖𝑎𝑟 como 𝑆𝐺 = 𝐴𝑝𝑜𝑦𝑜 con una probabilidad cero (ya que estas estrategias resultan
eliminadas). De igual forma, notamos que los Campesinos elegirían 𝑆𝐶 = 𝐴𝑝𝑜𝑦𝑜 con probabilidad cero.
Por otra parte, de la matriz reducida podemos concluir que los campesinos son indiferentes entre
𝑆𝐶 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑜 y 𝑆𝐶 = 𝑅𝑒𝑛𝑒𝑔𝑜𝑐𝑖𝑎𝑟
siempre que el gobierno elija 𝑆𝐺 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑜.
Podemos definir p como la probabilidad con que el Gobierno elige 𝑆𝐺 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑜. Por otra parte,
podemos definir q como la probabilidad con que los Campesinos elijen 𝑆𝐶 = 𝑆𝑢𝑏𝑠𝑖𝑑𝑖𝑜 y (1-q) como la
probabilidad con que éstos eligen 𝑆𝐶 = 𝑅𝑒𝑛𝑒𝑔𝑜𝑐𝑖𝑎𝑟. Tomando tales probabilidades, y en consonancia
con el análisis realizado en el anterior párrafo, podemos concluir que el juego tiene infinitos Equilibrios
de Nash, los cuales están dados por la siguiente expresión
𝐸𝑁 = {(𝑝 = 1, 𝑞)| 𝑞 ∈ [0,1]}
2.d)
Tomando la matriz inicial de pagos podemos concluir que la combinación (𝑆𝐺 = 𝐴𝑝𝑜𝑦𝑜, 𝑆𝐶 = 𝐴𝑝𝑜𝑦𝑜)
constituye un óptimo social. Lo anterior es cierto tanto desde una perspectiva utilitaria como desde una
perspectiva de Pareto. Por un lado, la suma de los pagos (20+10) es siempre mayor a la suma de los pagos
dados por los EN (pues dado un 𝑞 ∈ [0,1], tenemos que 30 > 15(1-q) + 5q +5). Por el otro, notamos que
cada jugador podría mejorar su utilidad individualmente (dado que 20>15(1-q) + 5q y que 10>5).
El hecho de que no coincidan con el Equilibrio de Nash indica que, dada la estructura de pagos de los
jugadores, en este juego la optimalidad entendida como la coincidencia de mejores respuestas no
corresponde a otras formas de entender la optimalidad (por ejemplo, como un concepto de optimalidad
individual en un sentido absoluto –el mejor pago posible que los agentes pudieron haber obtenido-, ni
como un concepto de optimalidad en sentido social ni de equidad).
Lo anterior no implica que el EN falle intrínsecamente como criterio de optimalidad en cuanto a su
coincidencia con un óptimo social (i.e., no es preciso decir que los agentes de este juego están en contra
del bienestar social). Lo único que este resultado implica es que, dada la estructura de pagos, los
individuos no van a tener incentivos a desviarse unilateralmente de estos Equilibrios de Nash, así existan
una combinación de estrategia distinta que provea unos mejores pagos tanto individual como
socialmente.








