Recuperatorio - 23 noviembre 2012
Anuncio

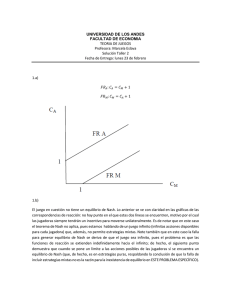
MICROECONOMÍA 2 EXAMEN RECUPERATORIO 23/11/2012 Registro . . . . . . . . . . . . Apellido y Nombres . . . . . . . . . . . . . . . . . . . Primer examen parcial 1. Una empresa dispone de un cine en una localidad en la cual existen dos grupos de consumidores potenciales. El primer grupo engloba a la población trabajadora con rentas elevadas y con una curva de demanda sobre películas de cines de X1D= 300-P. El segundo grupo está formado por consumidores jubilados con rentas bajas y con una curva de demanda de X2D= 180-P. La función de costos es C(x)= 40. Obtenga el equilibrio del monopolista que puede discriminar precios en los dos mercados. 2. 1) Comente las semejanzas y diferencias entre los modelos de oligopolio de Cournot y Stackelberg. 2) La demanda de mercado de los duopolistas viene dada por P(Y)=36-3Y. Los costos totales de cada una de las empresas son iguales a cero. 2. a. Hallar las cantidades, precio de equilibrio y dupolistas en un duopolio de Cournot. 3. Considere el cambio en el vector de precios de dos bienes: de P = [p1, p2] a P’ = [p1’, p2’]. Exprese la variación equivalente y variación compensatoria para el cambio en ambos bienes en términos de la suma de integrales bajo las correpondientes curvas de demandas hicksianas. Desarrolle el significado de estos conceptos como medidas del bienestar del consumidor. 4. A partir de las siguientes identidades que surgen del problema del consumidor deduzca la ecuación de Slutsky y explique qué representa. Represente gráficamente, mostrando los Efectos Renta y Sustitución en el caso de una función de utilidad sobre el consumo de dos bienes, cuando el precio de uno de ellos se modifica: a. b. c. d. E [p ,v (p,w)]=w V (p,w)=V[p, e(p,v)]=U* Xi*(p, w*)=Hi*[p, v(p,w*)] Hi*(p,u)=Xi*[p, e(p,u)] donde “e” es la función de mínimo gasto, “v” es la función de utilidad indirecta, “Xi” es la función de demanda marshalliana del bien “i”, “Hi” es la función de demanda hicksiana del bien “i”. 5. Explique cuáles son los problemas que, según Milton Friedman, tiene la asignación de un fin no vinculado con la rentabilidad en una empresa dentro de un sistema capitalista. 6. ¿Qué es un mercado perfectamente disputable? Compárelo con un mercado perfectamente competitivo. Segundo examen parcial 1. Considere un modelo en el que los consumidores están distribuidos uniformemente en el intervalo [0,1]. Suponga que existen dos firmas diferenciadas espacialmente. La firma 1 se encuentra en el punto 0 y la firma 2 se encuentra en el punto 1. Un consumidor ubicado en el punto x є [0,1] tiene una valuación por una unidad del bien provisto por la firma 1 y una valuación por una unidad del bien provisto por la firma 2. Cada consumidor desea comprar sólo una unidad. Adicionalmente, es suficientemente alto de forma que el consumidor siempre compra una unidad de alguna de las dos firmas. Las firmas enfrentan costos marginales constantes y con . Las firmas eligen precios y simultáneamente. a) Encuentre las funciones de demanda que enfrenta cada firma para cada combinación de precios. Ayuda: encuentre el consumidor que está indiferente y luego identifique los conjuntos de consumidores que demandan una unidad de cada firma. b) Encuentre los precios que maximizan los beneficios de las firmas 1 y 2, tomando, para cada paso, los precios de la firma rival como dados. 2. Considere un juego de dos jugadores en el que cada uno debe anunciar simultáneamente un monto de 0, 50 o 100 pesos. Si sus anuncios suman $100 o menos, entonces cada jugador se llega el monto que eligió. En caso contrario, cada jugador debe pagar $10. a) Plantee la forma extensiva del juego y la forma normal. b) Verifique si hay estrategias estrictamente dominadas c) Encuentre todas las estrategias racionalizables d) Encuentre todos los equilibrios de Nash. 3. Dos integrantes de un matrimonio han decidido salir a la noche. El problema es que ninguno recuerda cuál es el lugar al que habían acordado ir. Las actividades disponibles son ir al cine o ir al teatro. La mujer (jugador 1) prefiere el teatro, mientras que el hombre (el jugador 2) prefiere el cine. Así, en el caso de que se encuentren en el teatro, le reporta una utilidad de 2 y 1 respectivamente. Mientras que ir al cine, le reporta un pago de 2 al hombre y 1 a la mujer. En caso de que no se encuentren, ambos obtienen una utilidad de cero. a) Represente el juego en forma normal y en forma extensiva b) Halle los equilibrios de Nash en estrategias puras c) Suponga ahora que se introduce la posibilidad de estrategias mixtas: Halle las funciones de mejor respuesta para el hombre y para la mujer y obtenga el equilibrio de Nash en estrategias mixtas (recuerde graficarlo). 4. Explique la oposición complementaria entre burocracia y legislatura, según los distintos enfoques ofrecidos dentro de la teoría de la elección pública. 5. Utilice el concepto de punto de equilibrio de Schelling (o focal) para analizar el problema de la justicia y las instituciones. 6. Formule un problema de regulación de un mercado eléctrico en una economía capitalista.