AUTOEVALUACIÓN
Anuncio

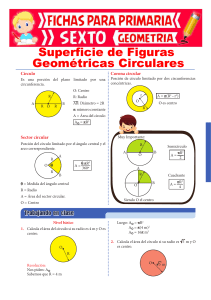
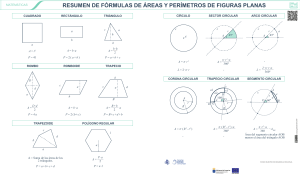
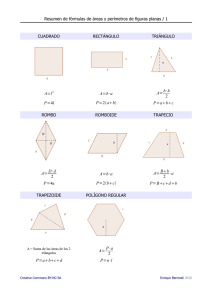
AUTOEVALUACIÓN 13.A1. Calcula el perímetro y el área de la siguiente figura. Perímetro = 12 · 1 + 8 · Área = 16 + 2 = 23,31 cm 1 2 · 8 = 20 cm 2 13.A2. ¿Qué longitud debe tener una escalera para que alcance la altura de 10 metros, si su base se apoya a 3 metros de la pared? La escalera forma con el muro y el suelo un triángulo rectángulo en el que ella es la hipotenusa. Utilizando el teorema de Pitágoras: e = 3 + 10 ⇒ e = 109 ⇒ e = 2 2 2 2 109 = 10,44 m. La escalera debe tener una longitud de 10,44 m. 13.A3. *Calcula el área de estas figuras planas cuyas medidas vienen dadas en centímetros. a) a) b) A= b⋅a 6⋅4 2 = = 12 cm 2 2 b) A= p ⋅ a n ⋅ l ⋅ a 7 ⋅ 3 ⋅ 3,11 2 = = = 32,66 cm 2 2 2 13.A4. Calcula la longitud de una semicircunferencia sabiendo que el diámetro mide 24 decímetros. L= 2 ⋅ π ⋅ r = 2 ⋅ π ⋅ 12= 75,4 dm 13.A5. Halla el área de una corona circular de 8,2 centímetros de radio mayor y 5 centímetros de radio menor. A = π · (R – r ) = π · (8,2 – 5 ) = 132,71 cm 2 2 Unidad 13 | Longitudes y áreas 2 2 2 13.A6. Calcula el área de las siguientes figuras. a) b) π ⋅ r 2 ⋅ nº π ⋅ 92 ⋅ 120º 2 = = 84,78 cm 360º 360º a) Asector circular = b) La figura es la mitad de una corona circular de radio mayor 2 cm y radio menor 0,5 cm. A= ( π ⋅ R2 − r 2 2 ) = π ⋅ (2 2 − 0,52 2 ) = π ⋅ 3,75 = 5,89 cm 2 2 13.A7. Averigua el área de estas figuras. a) a) b) La figura está formada por un rectángulo y un trapecio isósceles. 2 Arectángulo = b · h = 10,2 · 8,5 = 86,7 cm (2,1 + 10,2 + 2,1) + 6,4 B+b 2 Atrapecio = ⋅ 8,5 = 10,4 · 8,5 = 88,4 cm ⋅h= 2 2 El área de la figura es: A = Arectángulo + Atrapecio = 86,7 + 88,4 = 175,10 cm b) 2 Esta figura está formada por un trapecio isósceles y un triángulo. 9,6 + 3,2 B+b 2 Atrapecio = ⋅ 4,5 = 28,8 cm ⋅h= 2 2 b ⋅ a 9,6 ⋅ 13,5 2 = = 64,8 cm 2 2 2 El área de la figura es: A = Atrapecio + Atriángulo = 28,8 + 64,8 = 93,6 cm . Atriángulo = 13.A8. Un solar cuadrado mide 1600 metros cuadrados. ¿Cuántos metros mide su lado? = l = 1600 40 m Unidad 13 | Longitudes y áreas








![• (1JJ [b [M]](http://s2.studylib.es/store/data/001660247_1-1b1ec3f2af6ce5b36615782edea2e40e-300x300.png)