Taller Integración Numérica Archivo

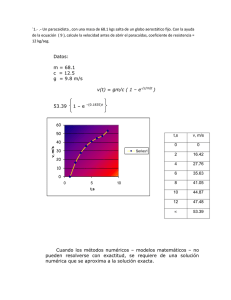
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
EJERCICIOS DE APLICACIÓN DE DIFERENCIACIÓN E INTEGRACIÓN
NUMÉRICA
1
APLICACIONES.
1. La siguiente ecuación representa un movimiento sobreamortiguado de un sistema
masa – resorte:
dx 2
dx

2

 2x  0
2
d t
dt

,  es la constante de amortiguamiento, m = es la masa del objeto, m
m
2
= 1.5 Kg. y  es el valor de la constante del resorte por unidad de masa. Si tenemos
2
que  = 4 y los datos tabulados a continuación
Donde 2 
t
x(t)
0.2
1.0650
0.35
1.0101
0.4
0.9826
0.6
0.8542
0.7
0.7871
0.8
0.7217
1.0
0.6009
Utilice las fórmulas de diferenciación numérica de mayor precisión posible, evaluadas
en el dato adecuado para determinar el valor de  .
NOTA: el valor de  es constante, así que debe ser el mismo si se evalúa en
cualquier punto, pero tenga en cuenta que al tratarse de un método numérico se
puede presentar pequeñas diferencias si es evaluada en datos diferentes.
2. La curvatura de una curva está dada por :
k (t ) 
Use la fórmula de diferenciación numérica de
mejor precisión para aproximar el valor de K(1)
con h=0.05, si:
2
x  2t y y  t  1
  dx   d 2 y   dy   d 2 x  

 2   
  2 
  dt   dt   dt   dt  
  dx  2  dy  2 

 
 
  dt   dt  
3
2
3. Según el análisis cinemático de del movimiento curvilíneo de una partícula en el plano,
el radio de curvatura en cualquier punto de la trayectoria se calcula a partir de
 
1  y 
2
3
2
y
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
EJERCICIOS DE APLICACIÓN DE DIFERENCIACIÓN E INTEGRACIÓN
NUMÉRICA
Utilice las fórmulas de diferenciación numérica para aproximar ρ en la posición x en la
cual se pueda aplicar la de mayor exactitud posible para los siguientes datos.
x
0
2
5
8
y
0
0.2
1.25
3.2
4. Se tomó la posición de un avión caza sobre un portaviones durante el aterrizaje:
t (s)
x (m)
0
154
0.51
174
1.03
187
1.74
220
2.36
235
3.24
253
3.82
286
4.15
296
Use la fórmula de diferenciación numérica de mayor precisión posible para determinar:
a. La velocidad (dx/dt) en x=220 m.
b. La aceleración (dv/dt) en x=235 m .
5. Un aeroplano es seguido por un radar, y cada segundo se registran los datos
siguientes en coordenadas polares θ y r.
t, s
θ, rad
r, pies
100
0,75
5120
101
0,72
5370
102
0,7
5560
103
0,68
5800
104
0,67
6030
105
0,66
6240
Emplee la fórmula de diferenciación numérica compuesta de mayor exactitud posible
para encontrar la expresión vctorial de la velocidad ( ) y la aceleración ( ) a los 103
segundos. La velocidad y la aceleración en coordenadas polares están dadas por:
⃗=
̈−
⃗ = ̇⃗ +
̇
̇⃗
⃗ + ( ̈ + 2 ̇ ̇) ⃗
6. La ley de Faraday caracteriza la caída de voltaje a través de un inductor como
Donde VL
=
= caída de voltaje (V), L = inductancia (en henrios,
=1
.
), i =
corriente ( A ), y t = tiempo ( s ). Determine la caída de voltaje, como una función del
tiempo a partir de los siguientes datos, para una inductancia de 4 H.
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
2
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
EJERCICIOS DE APLICACIÓN DE DIFERENCIACIÓN E INTEGRACIÓN
NUMÉRICA
t
i
0
0
0,1
0,15
0,2
0,3
0,3
0,55
0,5
0,8
0,7
1,9
7. La forma de un estacionamiento es irregular, y su longitud de oeste a este (izquierda a
derecha) es de 240 m. En el lado oeste la anchura es de 150 m y en el lado este es de
175. A 40, 80, 120, 160, 200 metros del lado oeste las anchuras son de 154, 158, 165,
163 y 172 metros respectivamente. Utilice la Fórmula de integración numérica
compuesta de mejor aproximación posible para determinar el área del
estacionamiento.
8. Un flujo que se mueve a través de un tubo de 12 pulgadas de diámetro tiene el
siguiente perfil de velocidades:
r
u
0
3
1
2,92
2
2,78
3
2,61
3,5
2,36
4
1,78
4,5
1,40
5
0,67
5,5
0,25
6
0
Encuentre la tasa volumétrica del flujo Q, usando la relación
Q=
2π r u dr
Donde r es el radio axial del tubo, R es el radio del tubo y u la velocidad. Utilice la
combinación adecuada de las fórmulas de Newton – Cotes cerradas para aproximar el
valor de Q.
9. Para hallar la fuerza ejercida por el agua contra un lado de una placa en forma de
triangulo isósceles con base de 6 pies y altura de 3 pies que se sumerge verticalmente
con la base hacia arriba, 2 pies bajo la superficie del agua hay que resolver la
siguiente integral
F=
62,4 (5 − y) 2y dy
Utilice la fórmula adecuada de integración numérica compuesta para aproximar el
valor de la fuerza usando los siguientes datos:
x
y
0
0,5
1
1,25
1,5
2
2,25
2,5
3
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
3
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
EJERCICIOS DE APLICACIÓN DE DIFERENCIACIÓN E INTEGRACIÓN
NUMÉRICA
10. La siguiente fórmula sirve para determinar el trabajo mecánico cuando la fuerza y el
ángulo entre la fuerza y la dirección del movimiento varían en función de la posición:
=∫
[ ( )]
( )
.
Utilice la combinación adecuada de fórmulas de integración cerradas de Newton –
Cotes para determinar el trabajo W, si se tiene que:
( ) = 1.5 − 0.04
x
F(x)
( )
0
( ) = 0.8 + 0.125 − 0.009
2
4
6
+ (2 × 10 )
7
8
9
10
11. Un tanque cónico invertido de 5 pies de radio y 10 pies de altura se llena hasta 2 pies
del tope con aceite de oliva que pesa 57 lb/pie3. Utilice la fórmula de Newton – Cotes
Cerrada apropiada para aproximar el valor del trabajo “W” que se requiere para
bombear el aceite hasta el borde del tanque sabiendo que
=
y, pies
F(y), lb
0
1.6
2
57
(10 − )
4
3.2
4
(
∗
4.8
)
6
6.3
8
12. Un eje circular tiene un diámetro d (m) que varía con la posición axial x(m) según
d  0.02(1  x 2 ) / e x
0  x  3m
Una carga axial P de 300000 N se aplica en un extremo del eje, cuyo E = 2*106
N/m2. la elongación axial del eje está dada por:
x  P / E  1 / Adx
d 2
A
4
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
4
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
EJERCICIOS DE APLICACIÓN DE DIFERENCIACIÓN E INTEGRACIÓN
NUMÉRICA
Calcular x aplicando la regla de integración compuesta de mayor exactitud posible
con h=0.2
13. El radio de un elipsoide varía con la posición axial x según:

r  0.04 1  4 x 2

,
x   0.5,0.5 .
Hallar su área superficial utilizando la fórmula de integración compuesta más exacta
posible y un h = 0.2, si está dada por
s 
2
0. 5
 dr 
4r    dx
 dx 
2
 0. 5
14. Una mujer empleo 10 min para manejar desde su casa hasta el supermercado. en
cada intervalo de 1 min observó en el velocímetro los valores mostrados en la
siguiente tabla, donde v(t) Km/h fue la lectura en el velocímetro a los t min después de
que la mujer salió de su casa. utilice la fórmula de integración compuesta óptima para
aproximar la distancia desde la casa de la mujer hasta el supermercado.
v(t)
t
0
0
1
30
2
33
3
41
4
38
5
32
6
42
7
45
8
41
9
37
10
22
Preparado por: ING. JORGE MARIO PEÑA CONSUEGRA
5