capitulo 1 - Universidad de Concepción
Anuncio

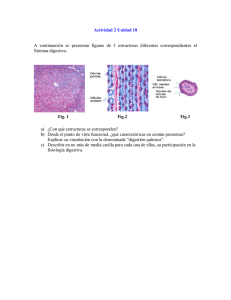
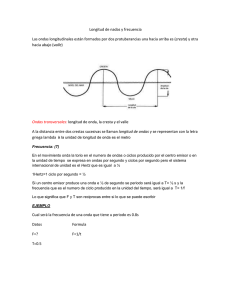
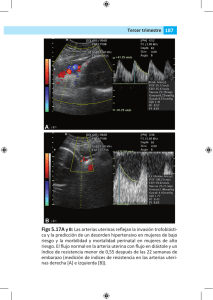
CAPITULO 1: ECUACIONES DIFERENCIALES PARCIALES DE PRIMER ORDEN Usando el método de las características, resolveremos problemas de valor inicial (PVI) para EDP de primer orden lineales, cuasilineales y no lineales en general, discutiendo el comportamiento de la solución en algunos ejemplos concretos. Este método está basado en una interpretación geométrica de la EDP que conduce a un sistema de ecuaciones diferenciales ordinarias (EDO) no lineal en general, y no siempre fácil de resolver. • ECUACIONES LINEALES Sean a, b, c, y d funciones suaves (o regulares) y consideremos la EDP lineal (EDPL) general de primer orden (1.1) a( x, t ) ∂u ∂u + b( x, t ) = c( x, t )u + d( x, t ), x ∈IR, t > 0. ∂x ∂t Idea del método: La solución u de (1.1) es una superficie en el espacio (x,t,u) que podemos parametrizar utilizando dos parámetros, digamos s y τ. Para hallar la expresión de u=u(x,t) suponemos dada una curva inicial C de parámetro τ, que será el dato inicial o condición inicial (CI) que acompaña a (1.1). Si por cada punto de C podemos trazar otra curva de parámetro s, entonces la superficie así determinada será la solución buscada. El lado izquierdo de (1.1) tiene la forma de una derivada direccional de u(x,t) en la dirección del vector [a, b] en los puntos (x,t) donde [a, b] esté definido y no sea nulo. Luego las ecuaciones (1.2) dx = a( x, t ); ds dt = b( x, t ) , ds s = parámetro, determinan una familia uniparamétrica de curvas en el plano (x,t): (1.3) x=x(s) ; t=t(s), cuyos vectores tangentes [x '(s), t '(s)] tienen la misma dirección de [a, b] (ver Fig.1). Por lo tanto la derivada total de u sobre las curvas (1.3) será (1.4) du ∂u dx ∂u dt = + ds ∂x ds ∂t ds ∂u ∂u a+ b ∂x ∂t = cu + d Luego tenemos el sistema de EDO = 1 Fig. 1 Derivada Direccional. dt du dx =a; =b; = cu + d, ds ds ds (1.5) llamado ecuaciones características de (1.1). Obviamente las dos primeras ecuaciones se pueden resolver independientemente de la tercera. Las soluciones de (1.5) son familias de curvas: x=x(s), t=t(s), u=u(s), llamadas curvas características (CC). Estas curvas en el plano (x,t) se llaman curvas características bases (CCB). Bajo hipótesis de suavidad sobre los datos a, b, c, y d, la teoría de EDO garantiza una única solución (x(s), t(s), u(s)), que será una CC del espacio (x,t,u) que pasa por un punto dado (x0, t0, u0). No estamos interesados en la solución general de (1.1) sino que en hallar una solución particular u = u(x,t) que será una única superficie en el espacio y que contenga una curva dada C. Esta curva será la CI para (1.1). La EDP y la CI constituyen un PVI o, más específicamente, un Problema de Cauchy. Método. Sea C la curva inicial dada paramétricamente por (1.6) C: x=x(τ) ; t=t(τ) ; u=u(τ), τ = parámetro. Para cada valor de τ tenemos un punto de C por el cual pasa una CC, La familia de curvas determinadas por los puntos de C está dada por: (1.7) x = x(s,τ) , t = t(s,τ) , u = u(s,τ) 2 tal que cuando s = 0 tenemos C, es decir, x(0,τ) = x(τ) , t(0,τ) = t(τ) y u(0.τ) = u(τ). Las ecuaciones (1.7) son una representación biparamétrica de una superficie en e espacio (x,t,u) que contiene a C. Resolviendo los PVI para las EDO (1.5): ì dx ï = a( x, t ) í ds ïî x s=0 = x( τ) ì dt ï = b( x, t ) í ds ïî t s=0 = t( τ) ì du ï = c( x, t )u + d( x, t ) í ds ïî u s=0 = u( τ) obtenemos: x=x(sτ), t=t(s,τ) y u=u(s,τ). Si de las dos primeras ecuaciones podemos despejar s y τ en función de x y t, y sustituyendo estos valores en u=u(s,τ), entonces obtenemos u(x,t). Esta función u(x, t) así conseguida satisface (1.1) en al menos una vecindad de C, y la CI (1.6). Además es la única solución del PVI. Fig. 2 Curvas características. Si este método no conduce a una solución entonces no existe o existen infinitas soluciones. Este último caso resulta si, por ejemplo, C coincide con una curva característica; este tipo de problema se conoce como "Problema de Valor Inicial Característico". 3 Ejemplo 1. Movimiento de ondas unidireccional. La EDP de primer orden ∂u ∂u (1.8) +c = 0 , c = cte., x ∈ IR, t > 0 ∂t ∂x representa un movimiento de ondas unidireccional en IR (conocida también como ecuación de convección). Resolveremos un PVI para (1.8) con la condición inicial (1.9) u(x,0) = F(x), x∈ IR siendo F una función dada. Sol: (1.10) Observando que la CI está dada a t=0, parametrizamos C como sigue: C: x=τ , t=0 , u=F(τ). Las ecuaciones características son: (1.11) dx =c, ds dt du = 1, =0 ds ds que, junto a las CI conforman los tres PVI para estas EDO, cuyas soluciones son (1.12) x(s,τ) = cs + τ , t(s,τ) = s , u(s,τ) = F(τ). Despejando τ y s en función de x y t en las dos primeras expresiones (1.13) s = t , τ = x - ct y sustituyendo en u(s, τ), obtenemos (1.14) u(x, t) = F(x - ct). Si F ∈ C1(IR) entonces (1.14) es la solución del PVI (1.8), (1.9). Notar que la solución está determinada sólo en términos del dato inicial. Interpretación física de la solución. Si F representa la forma inicial de una onda, entonces u(x, t) = F(x - ct) muestra que la onda no cambia de forma cuando t crece (e.d. a medida que el tiempo transcurre). Además, si c >0, entonces la onda "viaja" a la derecha con velocidad dx/dt = c; y si c<0 la onda "viaja" a la izquierda. Las CC son x-ct = τ. De este modo, para cada valor de τ, u es constante sobre las curvas características. Esto significa que el dato inicial se transmite a lo largo de las CCB, en el sentido que cualquiera sea el valor de u a t=0 en algún x, ese valor es el mismo en todos los puntos x pertenecientes a las CCB. 4 Fig. 3 Propagación unidireccional de ondas. Idea gráfica. Si el dato F(x) es la delta de Dirac δ(x), entonces la solución "formal" será u(x,t)=δ(x-ct), es decir, la solución es idénticamente nula salvo sobre las características sobre las cuales se propaga el dato inicial. Con todo lo anterior, ya podemos afirmar que las perturbaciones se propagan a lo largo de las curvas características bases. (Fig. 4) Fig. 4 Propagación de una perturbación (la función δ). 5 Si el dato F(x) es una función discontinua, por ejemplo u(x,0) = H(x+1) - H(x-1) siendo H(x) la función de Heaviside: (1.15) ì1, x > 0 H( x ) = í , î0, x ≤ 0 entonces la solución de (1.8) con c=1 tiene la forma u(x, t) = H(x+1-t) - H(x-1-t). Fig. 5 Propagación de discontinuidades. Del gráfico de esta última función, deducimos que no sólo las perturbaciones se propagan sobre las CCB, sino que también las discontinuidades (ver Fig. 5). Lo mismo ocurre en los puntos donde F(x) no es derivable. En efecto, basta considerar por ejemplo el dato inicial (1.16) ì0, x > 1 u(x,0)= R(x)= í î1 − x , x ≤ 1 entonces u(x, t) = R(x-ct), gráficamente indica que la propagación de los saltos de las derivadas ocurre sobre las CCB (ver Fig.6). De las ecuaciones características bases x-ct = τ = constante, deducimos que el dominio de dependencia de u(x,t) sobre el dato inicial está representado por u punto x=τ sobre el eje de las x. La influencia del dato inicial en un punto particular τ sobre la solución u(x,t), justamente son todos los puntos de la CC x-ct = τ. 6 Fig. 6 Propagación de los saltos de discontinuidad. NOTA: Este es un buen ejemplo para iniciar el estudio de la solución numérica por el método de las diferencias finitas. (Ver F John, " Partial Differential Equations", Springer Int. 1978). Ejemplo 2. Solución D'Alembert de la ecuación de ondas. El método de las características permite resolver un Problema en EDP para una ecuación lineal de segundo orden que rige el movimiento de ondas sobre IR con velocidad γ >0: (1.17) 2 ∂ 2u 2 ∂ u − γ = 0 , x ∈ IR , t > 0 ∂t 2 ∂x 2 Para tener un PVI agregamos las condiciones iniciales (1.18) (1.19) u (x,0) = f(x) ut(x,0) = g(x) siendo f y g funciones dadas. Para resolver (1.17) lo reescribimos como un sistema equivalente de EDP de primer orden. Para ello introducimos los operadores diferenciales ∂x, ∂t definidos por 2 ∂ 2u 2 ∂ u − γ = (∂ 2t − γ 2 ∂ 2x )u = (∂ t + γ∂ x )(∂ t − γ∂ x )u = 0 2 2 ∂t ∂x Sea (∂t - γ∂x)u = v, luego (∂t + γ∂x)v = 0. De este modo tenemos el sistema acoplado (1.20) 7 ∂u ∂u −γ = v( x, t ) ∂t ∂x (1.21) ∂v ∂v +γ =0 ∂t ∂x Debemos hallar la condición inicial para v(x, t). De la primera ecuación de (1.21) tenemos, a t=0, v(x, 0)= g(x) -γf ' (x). Luego el PVI para v(x, t) será ∂v ∂v +γ =0 ∂t ∂x v(x ,0) = g(x) -γf ' (x), cuya solución, de acuerdo al ejemplo 1, es v(x, t) = g(x -γt) - γf ' (x -γt). Sustituyendo en la primera ecuación de (1.21), tenemos el PVI para u(x, t): ∂u ∂u −γ = g( x − γt ) − γf ' ( x − γt ) ∂t ∂x u( x, 0) = f ( x ) (1.22) Ahora resolvemos (1.22) por el método de las características: dx =− γ , EDO: ds C: Luego, x=τ , dt =1 , ds t=0 , x = -γs+τ , t = s , du = g − γf ' ds u = f(τ). u= s ò (g − γf ' )dσ + f (τ) 0 Despejando τ y s en función de x y t de las dos primeras ecuaciones y considerando que f y g son funciones de x-γt , resulta : x+γs = τ Þ x-γs = τ -2γs, s u(s , τ) = ò [g( τ − 2γσ) − γf ' ( τ − 2γσ)]dσ + f ( τ) . 0 Sea λ = τ - 2γσ, dλ = -2γdσ. Luego, u(s, τ) = − 1 2γ ò − 2 γs + τ τ g(λ )dλ + 1 − 2 γs + τ f '(λ )dλ + f ( τ) 2 òτ = − 1 −2 γs+ τ 1 g(λ )dλ + [ f ( −2γs + τ) − f ( τ)] + f ( τ) ò τ 2γ 2 = − 1 −2 γs+ τ 1 g(λ )dλ + f ( −2γs + τ) + f ( τ) ò 2γ τ 2 es decir, 8 x − γt 1 [f ( x − γt) + f ( x + γt)] − 1 òx+ γt g(λ)dλ 2 2γ y de aquí resulta la solución D'Alembert de la ecuación de ondas u(s, t) = 1 [f ( x − γt) + f ( x + γt)] + 1 2 2γ Interpretación física de la solución. (1.23) Sea G(z) = u(x, t) = ò z ò x + γt x − γt g(λ )dλ . g(λ )dλ la antiderivada de g, luego (1.23) puede escribirse como é1 ù é1 ù 1 1 G( x + γt )ú + ê f ( x − γt ) − G( x − γt )ú . u(x , t) = ê f ( x + γt ) + 2γ 2γ ë2 û ë2 û El primer sumando de (1.24) representa ondas que viajan a la izquierda con velocidad γ, y el segundo sumando, ondas que viajan a la derecha con la misma velocidad. La expresión (1.23) (o bien (1.24)) nos dice que u(x, t) depende de los extremos del intervalo x ± γt a través del dato f(x), y de todos los puntos de ese intervalo a través del dato g(x). Luego, si por ejemplo g ≡ 0, la onda que se propaga sólo depende de los puntos x ± γt. Esta propiedad se expresa diciendo que no hay difusión de la onda, o que la onda se propaga sin difusión obedeciendo el Principio de Huygens. Interpretamos gráficamente esta doble propagación con los datos: g ≡ 0, γ =100, y f(x) es una onda suave con soporte en [-2, 2], tal como muestra la Fig. 7. (1.24) Fig. 7 Propagación bidireccional de ondas. Observamos que la onda no cambia de forma, tal como en el ejemplo 1. Sin embargo, hay una superposición al comienzo. Por cada décima de segundo la onda se traslada a 9 derecha e izquierda en una unidad de longitud y se suman las ondas obtenidas. Volveremos sobre esta ecuación más adelante. Ejemplo 3. Una ecuación con singularidades. Consideremos el PVI ∂u ì ∂u ïx +t = cu , c = cte. , x ∈ IR, t > 0 í ∂x ∂t ïî u( x, 1) = f ( x ) Observamos que el vector [x, t] es nulo en (0,0); es natural preguntarse entonces ¿cuál será el efecto de esta singularidad en la solución ? (notar que la condición inicial no está dada a t=0). (1.25) Sol. Tenemos los problemas en EDO: dx =x , ds x( 0 ) = τ cuyas soluciones son (1.26) (1.27) dt du =t = cu , ds ds t(0) = 1 u(0) = f ( τ) x(s, τ)= τes , t(s, τ)=es , u(s, τ)=f(τ)ecs (notar que no puede darse la condición inicial a t=0, pues en tal caso no podemos resolver el PVI para dt/ds=t). x y s = ln t, luego De aquí resulta τ = t æxö u(x, t) = f ç ÷ t c ètø es la solución de (1.25), pero no es válida para todo x y todo t. En efecto, (1.28) tiene una singularidad en t=0; basta considerar que si f es una constante k y c>0, entonces la solución u = ktc no ofrece problemas, pero si c<0 entonces la solución explota a t=0. (1.28) Ejemplo 4. Un problema con infinitas soluciones. Consideremos la EDP (1.25) con c=1, (1.29) x ∂u ∂u +t =u ∂x ∂t dx dt dx x =x y = t , resulta = , t ≠ 0 , de ds ds dt t donde x = αt, α=cte., son las curvas características bases (CCB), esto es, un haz de rectas que pasan por el origen (excepto el eje x). La ecuación característica para u será Combinado las ecuaciones características 10 du ds = du = u dt dt t ds de donde u = βt, β=cte. Debemos exigir u x =αt = β t con α, β fijados. Parametrizamos C como: τ æβö , u = ç ÷τ . α èαø De (1.26) y (1.27), para esta C, obtenemos las soluciones C: (1.30) x = τ, t= x(s, τ) = τes , æτö t(s, τ) = ç ÷e s , èαø æβö u(s, τ) = ç ÷τe s . èαø De las dos primeras ecuaciones de (1.30) no podemos despejar s y τ en función de x y t. Sin embargo, u = (β/α)x (=u(0, τ)) y u = βt (=u(αt, t)) son soluciones de (1.25). Luego no existe una única solución. Pero hay más, como β puede cambiar de una curva característica a otra, de u = βt se sigue que æxö u(x, t) = gç ÷ t ètø es una solución general de la EDP xux + tut = u, cualquiera sea g∈C1(IR); y como æxö g( z) z=α = β concluimos que gç ÷ t también es solución del PVI (1.25), es decir, ètø tenemos infinitas soluciones. Por otro lado, si las condiciones iniciales se dan sobre las CCB x = αt tal u no puede ser expresada como u =βt, entonces no existe solución. (1.31) NOTA: Técnicamente este problema no es un PVI-característico pues la curva C en el espacio (x,t,u) no es una curva característica. • ECUACIONES CUASILINEALES. Ahora estudiaremos una forma especial de EDP no lineal cuya forma general es (1.32) a(x,t,u) ∂u ∂x + b(x,t,u) ∂u = c(x,t,u), ∂t donde a, b y c son funciones dadas con cierta regularidad, digamos de C1 en x , en t y en u. En particular, dado que la no linealidad está dada sólo en los términos de mayor orden, la ecuación se llama cuasilineal. Un ejemplo típico de PVI asociado a una ecuación cuasilineal es el que modela el tráfico en carreteras: 11 ut + g(u)ux = 0 u(x, 0) = f(x), sobre el que volveremos más adelante. Tal como en el caso lineal, hallaremos la solución interpretando geométricamente la ecuación diferencial. Supongamos que existe una solución u=u(x,t) de (1.32), e.d., que existe una superficie integral que expresamos implícitamente como (1.33) F(x,t,u) = u(x,t) - u = 0. Tomando diferenciales obtenemos la ecuación de la tangente a F en todo punto ∂F ∂F ∂F dx + dt + du = 0 , ∂x ∂t ∂u e.d., uxdx+utdt-1du=0, de donde, tenemos la diferencial total du = uxdx+utdt. Luego, el vector normal a la superficie F(x,t,u)=0 en todo punto será: → ∇F ≡ n = [u x , u t , − 1] Por lo tanto (1.32) puede escribirse como (1.34) a ∂u ∂u é ∂u ∂u ù +b − c = [a, b, c ] ⋅ ê , , − 1ú = 0, ∂x ∂t ë ∂x ∂t û lo que implica que [a,b,c] pertenece al plano tangente a la superficie u=u(x,t) en todo punto (x,t,u) donde ∇F ≠ 0 . De este modo, la ecuación (1.32) puede considerarse como el requerimiento geométrico que toda superficie integral o solución u(x,t) que pasa por el punto (x,t,u) debe ser tangente el vector [a,b,c]. Si en algún punto de la superficie empezamos a movernos en la dirección del vector tangente conocido [a,b,c], lo hacemos sobre una curva que está completamente contenida en la superficie F(x,t,u)=0. Esta curva se llama característica, y hallando el conjunto de todas estas curvas características, hallamos la solución. ∧ ∧ ∧ Sea r = x i + t j + u k el vector posición de un punto sobre una curva característica. Siguiendo la idea de 1.1, expresamos paramétricamente r en términos de s (ver Fig. 8). Por lo tanto, el vector tangente a la curva en un punto particular será: dr dx ∧ dt ∧ du ∧ = i+ j+ k. ds ds ds ds Como los vectores [xs, ts, us] y [a,b,c] son tangentes a la curva, sus componentes son proporcionales, e.d., (1.35) dx dt du ds = ds = ds , a b c o bien 12 Fig. 8 Parametrización de una curva característica. (1.36) dx = a( x, t, u) ; ds dt = b( x, t, u) ; ds du = c( x, t, u) . ds Las ecuaciones diferenciales (1.36) son la ecuaciones características de (1.32) y sus soluciones son las curvas características de (1.32). NOTA: De la teoría de EDO sabemos que si a, b, c son suficientemente suaves y no se anulan en algún punto, entonces existe una única curva que pasa por cada punto (x0, t0, u0). La condición inicial para (1.32) resulta de especificar el valor de u(x,t) sobre una curva dada del plano (x,t), determinándose una curva C en el espacio (x,t,u), llamada curva inicial. Resolución del PVI: Para hallar la solución, pasamos una curva característica por cada punto de la curva inicial C. Si estas curvas generan una superficie, ésta superficie es la solución del PVI. Para reafirmar la existencia y unicidad de solución, damos el siguiente resultado: TEOREMA: " Sean a,b,c ∈ C1 en x,t,u. Sea C: x=x(τ), t=t(τ), u=u(τ), tal que C tenga vector tangente continuo y que (1.37) dt dx å ( τ) = dτ a[x( τ), t(τ), u(τ)] − dτ b[ x(τ), t(τ), u( τ)] ≠ 0 sobre C. Entonces existe una única solución u=u(x,t) definida en alguna vecindad de C satisfaciendo el PVI: 13 (1.38) ∂u ∂u ì ïa( x, t, u) + b( x, t, u) = c( x, tu) . í ∂x ∂t ïî u[ x( τ), t( τ)] = u( τ) " Idea de la demostración: De la teoría de EDO, sabemos que el sistema característico ì dx ï = a( x, t, u) í ds ïî u s=0 = x( τ) tiene una única solución (1.39) x = x(s,τ); ì dt ï = b( x, t, u) í ds ïî t s=0 = t( τ) ì du ï = c( x, t, u) í ds ïî u s=0 = u( τ) t = t(s,τ); u = u(s,τ) con derivada continua en s y τ tal que (1.40) x(0,τ) = x(τ) t(0,τ) = t(τ) u(0,τ) = u(τ). ìx = x(s, τ) en s=0 es El jacobiano de la transformación í î t = t(s, τ) ∂x ∂x ∂( x, t ) ∂s ∂τ = dt a − dx b (1.41) s =0 = s =0 = å ( τ ) ∂t ∂t dτ ∂(s, τ) dτ ∂s ∂τ que es distinto de cero por hipótesis, y por continuidad no se anula en una vecindad de C. Luego, por el teorema de la función implícita, podemos despejar s y τ como funciones de x y t cerca de C, e.d., (1.42) u(x,t) = u[s(x,t), τ(x,t)] es una solución del PVI (1.38). La unicidad resulta del hecho que dos superficies integrales cualesquiera, que contienen la misma curva inicial, coinciden sobre todas las CC que pasan por la curva inicial. NOTA: La hipótesis (1.37) significa que la curva inicial C no es característica ni es la envolvente de CC. Si C es una curva característica, entonces existe solución pero no es única. Si C es una envolvente entonces u puede o no ser diferenciable sobre C. Si C no es característica salvo en un conjunto discreto de puntos, entonces surgen problemas especiales en la vecindad de esos puntos. Ejemplo 5. Movimiento unidireccional no lineal de ondas. Consideremos el siguiente PVI 14 (1.43) ∂u ∂u ì ïEDP : +u =0 , í ∂t ∂x ïî CI : u( x,0) = f ( x ) siendo f(x) una función dada. SOL.: Parametrizamos C como sigue: (1.44) x=τ; t=0 ; u = f(τ) Aplicamos (1.37): å(τ) = -1. Las ecuaciones características son: dx dt du = u; = 1; = 0; ds ds ds du = 0 resulta que u=cte. sobre C, luego u(s,τ) = u(0,τ) = f(τ). Del hecho que ds Por lo tanto, dx dt ü ü = u = f ( τ)ï =1 ï Þ x ( s , τ ) = τ + sf ( τ ) y ds ds ý ý Þ t(s, τ) = s . ï ïþ x s =0 = τ t s =0 = 0 þ (1.45) Si u verifica la hipótesis del teorema, el sistema anterior puede invertirse cerca de C para dar: s = t ; τ = τ(x,t). Luego la solución será (1.46) u = f(τ(x,t)) y como s = t y τ= x- sf(τ)=x - tu, resulta (1.47) u = f(x - tu). Discusión física de la solución: Si u=u(x,t) representa una onda, entonces la forma de la onda, en todo instante, está dada por la curva u = u(x,t) en el plano (x, u) con t= parámetro y u = f(x) la forma inicial de la onda. Claramente el valor numérico de u(x,t) da la altura de la onda en x y a tiempo t. Cómo de mueve la onda?. Primero debemos hallar la velocidad dx/dt en cada punto. Las dos primeras ecuaciones de (1.45) dan (1.48) dx =u, dt e.d., la velocidad de propagación no es constante. Por lo tanto, a mayor amplitud de la onda, u(x,t), mayor velocidad (distinto al caso lineal !). Luego, si u>0 x va a la derecha; si u=0 x permanece fijo y si u<0 x va a la izquierda. Por lo tanto si u cambia de signo hay partes de la onda que van hacia la izquierda y otras a la derecha. En tal caso el viaje no es unidireccional. 15 Supongamos que u>0; luego los puntos x tal que u(x,t) es grande y la onda el "alta", se moverán más rápido que los puntos x donde u(x,t) tiene un valor menor y la onda es más "baja". Por lo tanto si a t=0 hay partes de altas de la onda a la izquierda de otros puntos, éstos pueden alcanzar los puntos bajos y pasarlos; ahí se produce el quiebre de la onda . Fig. 9 Quiebre de ondas. En el tiempo de quiebre (tq), u(x, t) es multívoca y deja de ser una solución válida para el PVI (pensar que si u representa una densidad, la multivocidad no tiene sentido). Por qué se produce tan desagradable suceso?. En general, porque en el modelo (1.43) se han despreciado términos con derivadas de mayor orden (existe un modelo mejor: la é æ γ + 1ö ù ecuación de Burger: u t + ê1 + ç ÷uúu x − εu xx = 0 . ë è 2 ø û Observación importante: El PVI ∂v ∂v D ∂ 2 v = −c + ∂t ∂x 2 ∂x 2 v(x,0)= δ(x), donde c y D son constantes y δ es la "delta de Dirac" , tiene como solución æ ( x − ct )2 ö ÷ v(x,t) = kexp çç − 2Dt ÷ø è que es muy regular para todo t >0. Pero si D=0 (e.d., consideramos la EDP de primer orden) la solución es v(x,t) = δ(x-ct) que es singular para todo t>0. Es decir, al incluir términos con derivadas de mayor orden en la EDP, la ecuación tiende a suavizar la solución. 16 NOTA: Existe otro método, llamado "ondas de choque discontinuo", que extiende la validez de la solución más allá del tiempo de quiebre (la ecuación de la onda de choque depende fuertemente del fenómeno en estudio). Volvamos al PVI (1.43). Volvamos al PVI (1.43): la forma de la onda depende del dato inicial, en particular si la onda se quiebra, también depende del dato inicial. Cabe preguntarse si es posible hallar el tiempo de quiebre tq. La respuesta es afirmativa y veremos dos métodos: 1er Método. Determinemos la pendiente de la forma de la onda u= u=(x,t)=f(x-tu) a tiempo t. Derivando implícitamente f ' ( x − tu) ∂u = . ∂x 1 + tf ' ( x − tu) De x(s,τ) = τ+sf(τ) ; t(s,τ) = s resulta que las curvas características bases (CCB) para (1.43) es la familia de rectas: x – tf(τ)= τ , siendo τ el parámetro. ∂u → ∞ y la onda Cuando 1+tf '(x-tu)=1+tf '(τ) se anula por primera vez, entonces ∂x empieza a quebrarse; luego (1.49) tq = - (1.50) 1 f ' ( τ) es el tiempo de quiebre. 2do Método. Recordemos que si F(x, t,τ)=0 es una familia uniparamétrica de curvas con parámetro τ, la envolvente se encuentra eliminando τ del sistema: ì F( x, t, τ) = 0 í îFτ ( x, t, τ) = 0 Considerando las curvas características x=τ+sf(τ); t=s. Resulta que u=f(τ) sobre las CCB (1.51) x – tf(τ)=τ , τ=parámetro. Si para dos o más valores de τ las rectas (1.51) se cortan., entonces u es multivaluada en el punto de intersección (pues u(x, t) debe ser igual a f(τ) en ese punto). Para hallar los puntos de intersección debemos determinar la envolvente de (1.51). F = x-tf(τ) - τ = 0 Þ Tenemos así: ∂F = -tf ' (τ) – 1 =0. ∂τ 17 x − tf ( τ) − τ = 0ü 1 , e.d., las ý Þ x-tf(τ) = τ, lo que da –tf '(x-tf(τ))=1, de donde t = − tf ' ( τ) − 1 = 0 þ f ' ( τ) 1 . veces que las CC tocan la envolvente está dado por t = f ' ( τ) 1 siempre es negativo y la onda no se quiebra. De (1.50), si f ‘(τ)>0 ∀ τ, entonces f ' ( τ) Geométricamente esto significa que u = f(x) es una función monótona creciente en x (ver Fig. 10). Fig. 10 No existe quiebre de la onda. Si f '(τ)<0 ∀ τ, entonces u=f(x) es monótona decreciente y los puntos más altos de la onda se mueven más rápido que los puntos bajos y pueden sobrepasarlos, produciéndose así el quiebre d la onda. (si f ' cambia de signo, generalmente hay quiebre de onda). Fig. 11 Existe quiebre de la onda. Hay otra interpretación de los resultados anteriores sobre el quiebre de la onda: De 18 1 y x - tf(τ) = τ siendo τ=parámetro, resulta que el tiempo de quiebre está f ' ( τ) determinado por el punto sobre la curva t=- f ( τ) 1 ;t=; u = f(τ), f ' ( τ) f ' ( τ) Donde t alcanza el mínimo valor, es decir, cuando el hessiano Cτïs=0 : x = τ - ∂x ∂s ∂t ∂s ∂x ∂t ∂t ∂τ = 0. s=0 Pero de (1.37) esto implica que å(τ)=0 en ese punto; luego si Cτ se elige como curva inicial C para la EDP ut+uux=0, el teorema no garantiza solución única. Además, f ' ( x − tu) C τ f ' ( τ) ∂u = = Þ u no es diferenciable sobre Cτ. ∂x 1 + tf ' ( x − tu) 1 − 1 Luego, aun cuando el dato inicial garantice solución única, ésta solución se quiebra si la condición å(τ)≠0 fuese violada. Esta curva quebrada no es una CC para la EDP pues u no es constante sobre ella. Finalmente, si la curva inicial es una CC entonces el PVI tiene infinitas soluciones. En efecto, recordemos que las ecuaciones características para nuestro problema son: dx dt du =u ; =1 ; =0. ds ds ds Luego la recta x=ct es una característica para la EDP pues con t=s, x=cs satisfacen las ECP. Sea u=c=cte. Sobre x=cxt. Entonces u=f(x-tu) es una solución del PVI, pero también los es f(0)=c. Tres ejemplos de f(x) para ut + uux =0. Ejemplo 6. Consideremos el dato inicial (1.52) u(x,0) = f(x) = -x. Como f '(x) = -1, la onda debe quebrarse, e.d. u será multívoca en algún punto. En efecto, como f(τ) = -τ, tq=1 es el tiempo de quiebre. x Además, u=f(x-tu) = -(x-tu) Þ u = -x +tu, es decir, u = es la solución del PVI t −1 ìu t + uu x = 0 , solución que explota en t=1. í î u( x,0) = − x En la Fig. 12 observamos el comportamiento de la solución de t=0 a t=t1, concluyendo: 19 i) existe una rotación alrededor del origen en el plano (x,u) ii) u crece linealmente respecto de x iii) t=1 Þ u = eje u (multivaluada allí) La multivocidad de u en t=1 también puede visualizarse considerando las CCB:x= (1-t)τ. iv) x . t −1 Para t = 1, todas las rectas se cortan en (x,t)=(0,1). A cada una de estas rectas le corresponde un valor de τ y como u(x,t) es constante sobre cada una de estas rectas, u será multívoca en t = 1 (ver Fig. 13) Fig. 12 Movimiento de la onda u = Fig. 13 Multivocidad de u en t=1 20 NOTA: Obviamente, si f(x)=x entonces u(x,t) = x está bien definida para todo t>0. t +1 Ejemplo 7. Consideremos ahora la CI: u(x,0)= f(x) = 1-x2. Usando la forma implícita u=f(x-tu) la solución es u=1-(x-tu)2 = 1-x2 +2xtu – u2t2, e.d., u2t2+u(1-2xt)+(x2-1)=0, de donde x 1 + ± 1 + 4 t( t − x ) − t 2t 2 Luego la solución tiene dos ramas. x 1 ± 1 + 4 t( t − x ) Si calculamos lim − ,debemos considerar el signo más en (1.53) para t →0 t 2t 2 que así u(x,t) verifique la CI u(x,0)=1-x2, luego (1.53) (1.54) de donde u(x,t) = x 1 + 1 + 4 t( t − x ) − , t 2t 2 ∂u 1 1 = + → ∞ si 1+4t(t-x)→0, e.d., ∂t t t 1 + 4t( t − x ) u= la pendiente ∂u →∞ ∂x cuando (1.55) x = t + 1 . 4t El radical en (1.54) es real si x<t+ 1 , luego u está bien definida ahí. Ahora, t>0; 4t 1 Þ x < 1, es decir, u está bien definida para x<1. En x=1, el radical se anula 4t para t=½ y cuando x→ +∞el tiempo t donde anula →0 (de (1.55)). Por lo tanto si la CI se da sobre todo IR, la onda empieza a quebrarse “inmediatamente” a x= +∞. Las CCB para este problema son: x<t+ (1.56) x-t(1-τ2) = τ , τ = parámetro y la envolvente de estas curvas es 1 =0 (idéntica a (1.56)) 4t Puesto que dos curvas cercanas de (1.56) se cortan sobre la envolvente para valores diferentes de τ, entonces u es doblemente valuada en (1.57). En efecto, la raíz en (1.54) se anula sobre (1.57) en el plano (x,t), es decir, u se divide en dos ramas dadas por (1.54) sobre (1.57). Una idea gráfica está dada en la Fig. 14. Un ejercicio interesante es estudiar el caso cuando el dato inicial se restringe al intervalo - ∞ < x ≤ a, a>1. (1.57) x–t- 21 Movimiento de la onda 1-x2 Fig. 14 Ejemplo 8. Consideremos ahora el dato inicial u(x,0)= f(x) = senx. Obviamente la solución es u= sen(x-tu) y las CC son x-tsenτ - τ = 0, y el tiempo de quiebre (usando 1 (1.50)) resulta ser tq = . cos τ Así, el menor valor de t ocurre a t = 1, es decir, tq=1. Una idea gráfica está dada en la Fig. 15. Fig. 15 Movimiento de la onda senx. 22 NOTA: La solución de ∂u ∂u + c(u) = 0, ∂t ∂x donde c(u) es una función arbitraria, no tiene un comportamiento muy diferente de la solución de (1.58) ∂u ∂u +u =0 ∂t ∂x ya que si (1.58) se multiplica por c '(u), resulta una ecuación para c(u) que tiene la misma forma de (1.59) con u reemplazada por c(u). (1.59) Ejemplo 9. Propagación de ondas de agua. De la discusión de los ejemplos anteriores puede deducirse que una ecuación cuasilineal puede ser un buen modelo para estudiar la propagación de ondas de agua superficiales. En efecto, sea u(x,t) la elevación de la superficie del agua respecto del nivel u=0 del agua en reposo. Si suponemos que esta elevación es pequeña como también ux y ut, la EDP que gobierna la propagación de ondas es (1.60) æ 3 ö ç 1 + u ÷u x + u t = 0 , − ∞ < x < +∞, t > 0 . è 2 ø Una CI apropiada es ìε(1 + cos x ), − π ≤ x ≤ π, 0 < ε << 1 í î 0, x > π Las ecuaciones características son (1.61) dx 3 dt du = (1 + u) ; = 1; = 0. ds 2 ds ds En lugar de parametrizar la CI como la curva C, seguimos otro camino. De (1.62) podemos escribir las ecuaciones características como (1.62) dt dx y du = 0 = 3 1 1+ u 2 Por lo tanto, sobre una característica (1.63) (1.64) dx 3 = 1+ u dt 2 y u = constante . dx también es constante ahí. Luego las dt características son rectas no paralelas. De (1.64), Como u es constante sobre una característica, 23 (1.65) 3 ì ï x − (1 + u)t = c 1 í 2 ïî u = c2 3 sobre una característica; por lo tanto, en general u = f(x-(1+ u)t). 2 De la CI (1.61) s sigue que ì é æ 3 ö ù æ 3 ö x − ç1 + u ÷t ≤ π ïε ê1 + cos( x − ç1 + u ÷ t )ú, ï è 2 ø û è 2 ø (1.66) u(x,t)= í ë æ 3 ö ï0 , x − ç1 + u ÷t > π. ïî è 2 ø æ 3 ö Luego, c2 = ε(1+cosc1) sobre x − ç1 + u ÷t = c 1 ≤ π , por ejemplo. La Fig. 16 muestra las è 2 ø æ 3π ö æ π ö CCB (1.65). Los valores de las constantes (c1, c2) = ç − ,0 ÷ , (-π,0), ç − , ε ÷ , è 2 ø è 2 ø ....determinan rectas características particulares. Fig. 16 Plano característico. La Fig. 17 muestra la propagación de los perfiles de ondas e ilustran el fenómeno no lineal del quiebre del frente de ondas. Para terminar, calculemos el tiempo de quiebre (por el primer método) 24 æ − ε sen η æ 3 ö öæ 3 ö ux = -εsen çç x − ç 1 + u ÷t ÷÷ç1 − u x t ÷ Þ u x = 3 è 2 ø øè 2 ø è 1 − tε sen η 2 3 æ 3 ö con η = x − ç 1 + u ÷ t . Claramente ux =∞ cuando 1 − tε sen η = 0 . 2 è 2 ø Como η es constante a lo largo de cualquier característica, esto ocurre primero sobre la π 2 recta cuando η = y así senη=1. Por lo tanto t q = . 2 3ε Estudie el caso para ε<0. Fig. 17 Propagación de perfiles Prof. Raúl F Jiménez Departamento Matemática Universidad de Concepción Marzo 2000. 25