Cap. 15. Árboles AA.

1
Capítulo 15
Árboles AA.
Mediante árboles binarios de búsqueda balanceados, se han desarrollado algoritmos eficientes
para mantener diccionarios, que garantizan un costo logarítmico de las operaciones en peor
caso.
Para desarrollar algoritmos para árboles AVL y árboles coloreados se requiere un análisis
cuidadoso de los diferentes y numerosos casos que se presentan, para implementar las
estrategias de rebalance luego de una inserción o un descarte.
Los árboles AA, así denominados por las iniciales de su creador, son una simplificación de las
reglas de los árboles coloreados y originan un número bastante menor de situaciones que deben
ser analizadas. Además de las reglas de los árboles coloreados, sólo se permiten nodos rojos
como descendientes derechos.
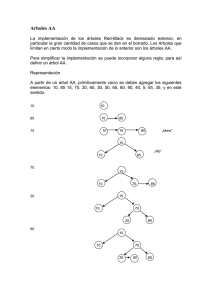
En estos árboles, en lugar de la información sobre el color, se almacena el nivel del nodo; las
hojas son de nivel 1. En lugar de color rojo se habla de enlace derecho horizontal, o de un nodo
descendiente derecho con igual nivel que su padre. La Figura 15.1, muestra las estructuras de
árboles AA, con número de nodos n, de uno a tres. A la derecha se muestra el nivel de los
nodos.
n=1
1
0
n=2
1
0
2
n=3
1
0
Figura 15.1. Árboles AA, de hasta 3 nodos.
15.1. Propiedades de los árboles AA.
El nivel de un hijo izquierdo debe ser menor que el nivel de su padre.
El nivel de un hijo derecho debe ser menor o igual al nivel de su padre.
El nivel de un nieto derecho debe ser menor que el nivel de su abuelo.
Las hojas son de nivel 1.
Los nodos que no son hojas deben tener dos hijos.
Profesor Leopoldo Silva Bijit
20-01-2010
2
Estructuras de Datos y Algoritmos
El número de nodos visitados, desde la raíz hasta las hojas, por la vía más larga debe ser a lo
más el doble del número de nodos recorridos por la vía más corta. Esto asegura un costo
logarítmico para las operaciones.
15.2. Análisis de la operación inserción.
Un nuevo nodo que será de nivel 1, se inserta en las hojas, que también son de nivel 1.
Se presentan dos casos.
a) Si se inserta por la izquierda se viola la regla de sólo horizontales derechos, y debe efectuarse
una rotación derecha.
Descendiendo desde la raíz, se determina la posición para insertar, ésta se muestra con una
flecha, en la Figura 15.2, superior. Al centro, se muestra una representación convencional, con
un nodo descendiente horizontal izquierdo. En la parte inferior se muestra luego de una rotación
derecha, respecto del padre del nodo insertado; ahora se cumplen las propiedades de un árbol
AA. Se definió esta operación como torcer (skew).
1
1
1
Figura 15.2. Inserción por la izquierda. Skew.
La inserción por la izquierda seguida de una torsión, puede originar una nueva violación a las
propiedades de los árboles AA. Esto se ilustra en la Figura 15.3 en la parte superior; luego se
dibuja en forma convencional, de acuerdo a los niveles de los nodos. La tercera ilustración
muestra la situación luego del skew; lo cual produce el doble rojo, o dos hijos horizontales, debe
notarse que el recién insertado es la nueva raíz. La situación se corrige con una rotación a la
izquierda, respecto del nodo recién insertado, y luego incrementando el nivel del nodo central;
lo que se muestra en el diagrama inferior de la Figura 15.3. Esta última operación se denomina
partir (split), y se deriva de los B-trees antecesores de los árboles AA, en los cuales se divide un
multinodo que excede el máximo número de claves en dos multinodos.
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
3
1
1
1
2
1
Figura 15.3. Inserción por la izquierda. Skew y split en el mismo nivel.
Puede observarse que cuando se ejecuta un skew seguido de un split, en el mismo nivel de
recursión, puede simplificarse la secuencia evitando las rotaciones, ya que basta incrementar el
nivel del nodo raíz en el segundo diagrama; pasando de este modo al diagrama inferior de la
Figura 15.3.
Otra situación de inserción por la izquierda se muestra en la Figura 15.4. Luego de un skew en
el padre del recién insertado resulta el diagrama al centro. Y al retornar por la vía por la cual se
descendió para insertar, debe efectuarse un split en el nuevo padre del recién insertado,
resultando el diagrama inferior de la Figura 15.4. Nótese que el skew y el split se aplican en
nodos diferentes, en dos niveles de recursión.
1
1
2
1
Figura 15.4. Inserción por la izquierda. Skew y split en niveles de recursión diferentes.
b) Si se inserta por la derecha, si el padre no tiene descendiente derecho no hay modificaciones
que efectuar, lo cual se muestra a la izquierda de la Figura 15.5; pero si el padre es un
descendiente derecho se producen dos descendientes horizontales, la situación equivale a dos
rojos adyacentes, y se corrige efectuando una rotación a la izquierda, e incrementando en uno el
nivel del nodo central; es decir con un split. No se requiere en este caso de la operación skew.
Profesor Leopoldo Silva Bijit
20-01-2010
4
Estructuras de Datos y Algoritmos
1
1
1
2
1
1
Figura 15.5. Inserción por la derecha.
La operación split, al subir el nivel de un nodo, puede ocasionar un nuevo descendiente
izquierdo de igual nivel que el padre o tres nodos adyacentes de igual nivel. Por esta razón debe
ascenderse hasta la raíz, siguiendo la ruta por la que se descendió, para ubicar la posición de
inserción, efectuando las operaciones skew y split, en ese orden, en cada uno de los nodos de la
ruta.
Sin embargo, como se verá más adelante, en cada nivel de recursión, cuando debe efectuarse
una modificación para mantener las propiedades sólo se efectúa un skew o un split o un
incremento de nivel.
Se han analizado las diferentes situaciones de inserción que se producen en el primer nivel de un
árbol AA. Esto se logró efectuando inserciones en un árbol con un nodo, e inserciones en un
árbol con dos nodos.
Aplicando las operaciones anteriores, puede comprobarse la estructura de los árboles AA, para
4, 5, 6 y 7 nodos que se muestran en la Figura 15.6. Debe notarse que en cada diagrama hay
que estudiar (n+1) casos de inserción, ya que éste es el número de nodos externos, o los posibles
lugares para insertar el nuevo nodo.
Sin embargo si se observan las formas que se producen en los diferentes niveles de la Figura
15.6, puede deducirse que los casos de inserción analizados antes son los únicos que se
presentan.
2
n=4
1
2
n=5
1
2
n=6
1
3
2
n=7
1
Figura 15.6. Formas de árboles AA para 4, 5, 6 y 7 nodos.
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
5
15.2.1. Ejemplos de inserción.
Si se realiza una inserción de claves en orden ascendente, desde el 1 hasta el 15, se obtiene
luego de las operaciones de rebalance, después de cada inserción, la Figura 15.7,
inmediatamente luego de insertado el nodo con valor 15.
Se devuelve siguiendo la ruta desde la raíz al nodo insertado, pero en forma ascendente. Como
el nodo 15 cumple las propiedades, es un árbol AA; se asciende al 14, que también es AA. Pero
al ascender al 13, éste tiene dos hijos horizontales; entonces debe realizarse un split en el nodo
13, con lo cual resulta la Figura 15.8. El árbol cuya raíz es el nodo con valor 14 es AA, notar
que ésta es la raíz luego del split.
Figura 15.7. Inserción de nodo con valor 15 en árbol AA.
Figura 15.8. Luego de split en nodo con clave 13.
Al ascender al nodo con valor 12, también se cumplen las propiedades de los árboles AA. Pero
al ascender al nodo con valor 10, debe volver a efectuarse un split, resultando la Figura 15.9.
Profesor Leopoldo Silva Bijit
20-01-2010
6
Estructuras de Datos y Algoritmos
Figura 15.9. Luego de split en nodo con clave 10.
Continuando el ascenso, no es necesario efectuar correcciones en el nodo con valor 8, pero al
ascender a la raíz, debe volver a efectuarse un split, resultando la Figura 15.10; que muestra un
árbol perfectamente balanceado, con raíz 8. En secuencias de inserciones ascendentes sólo es
necesario realizar operaciones splits.
Figura 15.10. Luego de split en nodo con clave 4.
Estudiemos ahora una inserción de secuencias descendentes de claves. Se han insertado, en
forma descendente las claves desde 15 a 9, y luego se han efectuado las operaciones de
mantención. La Figura 15.11, a la izquierda, muestra la inserción de un nodo con clave 8; lo
cual produce un descendiente izquierdo de igual nivel que su padre, por lo cual debe efectuarse
un skew, al ascender al nodo 9. A la derecha de la Figura 15.11, se muestra el árbol AA
resultante, ya que al recorrer la ruta ascendente, pasando por el 10 y llegando a la raíz 12, no es
necesario efectuar mantenciones.
Figura 15.11. Luego de insertar el 8, y luego de skew en 9 y ascender hasta la raíz.
Si en el árbol AA de la Figura 15.11, a la derecha se inserta un nodo con valor 7, se tiene el
diagrama a la izquierda de la Figura 15.12.
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
7
Figura 15.12. Luego de insertar el nodo con valor 7 y luego del skew en 8.
Se efectúa un skew en 8, luego de la operación se tiene el diagrama a la derecha de la Figura
15.12; y es preciso efectuar un split en 7. Luego de esta operación resulta el diagrama a la
izquierda de la Figura 15.13. El cual podría haberse obtenido sin rotaciones, incrementando el
nivel del nodo con clave 8, en la Figura 15.12 a la izquierda.
Al ascender al nodo 10, la operación anterior produce un hijo izquierdo de 10 de igual nivel, lo
cual implica un skew en 10. Luego de esta operación y al ascender a la raíz, no son necesarias
más operaciones para mantener las propiedades de los árboles AA. Lo cual se muestra en la
Figura 15.13, a la derecha.
Figura 15.13. Luego de split en 7, y luego del skew en 10.
Puede comprobarse que luego de las inserciones de los nodos 6 a 1, y de las posteriores
verificaciones del cumplimiento de las propiedades, resulta la Figura 15.10.
15.2.2. Diseño de las operaciones skew y split.
Las operaciones pueden efectuarse de manera recursiva o de arriba hacia abajo.
La operación torcer (skew) elimina los hermanos horizontales izquierdos bajo el nodo. Se
desciende por la derecha efectuado rotaciones derechas cuando se encuentra un enlace
izquierdo.
Si un nodo tiene más de un hermano derecho de igual nivel debe partirse (split), aumentando el
nivel de cada segundo nodo en el descenso. Se desciende por la derecha, efectuando rotaciones
izquierdas.
Debido a que tanto la inserción como el descarte requieren recorrer una ruta desde la raíz hasta
las hojas, es preferible realizar la mantención de las propiedades de los árboles AA, desde abajo
hacia arriba, efectuando operaciones a medida que se asciende por la ruta de descenso. Para
Profesor Leopoldo Silva Bijit
20-01-2010
8
Estructuras de Datos y Algoritmos
lograr esto las operaciones skew y split pueden implementarse como procedimientos actuando
sobre un nodo solamente. Como se verá más adelante esto implica invocar tres veces a torcer y
dos veces a partir en cada nodo en la operación descartar; y una vez a torcer y partir en cada
nodo en la operación insertar.
Podemos analizar en general la inserción, asumiendo que el subárbol apuntado por t, es AA en
el lado en que no se realizó la inserción y que su raíz tiene nivel i. Por otro lado, el subárbol
cuya raíz es n, donde se realizó la inserción es AA, ya que se ha logrado reestablecer las
propiedades en los niveles inferiores. Mediante el puntero t, se recorre la ruta ascendente hacia
la raíz.
Si el nivel de n es menor que i, no es necesario seguir revisando la ruta ascendente.
15.2.3. Inserción por la izquierda.
a) B de nivel i.
Si el subárbol derecho era AA, los nodos C y D deben tener nivel (i-1). En la Figura 15.14, se
muestra el nodo n de nivel i, lo que viola las propiedades de un árbol AA, y la estructura debe
ser corregida. Según se analizó antes, la única forma en que un nodo aumenta su nivel es
teniendo ambos hijos de igual nivel. Entonces si antes de insertar el nodo n el árbol era AA, y si
el nodo n alcanza grado i quiere decir que lo ha logrado teniendo hijos de igual nivel. Esto
implica que a y b deben ser de nivel (i-1). Si A tiene padre debe ser de nivel (i+1).
t
a
A i
n
i
i-1
b
B
i-1
i
C i-1
D i-1
Figura 15.14. Inserción por la izquierda. B de nivel i.
En este caso luego de un skew en t, resulta el diagrama a la izquierda de la Figura 15.15; y luego
del split en el nuevo t, resulta el subárbol AA a la derecha de la Figura 15.15. En este caso,
debido a que el nodo A aumenta su nivel inicial, es preciso continuar la revisión ascendente. La
situación puede ser corregida, sin realizar rotaciones, cambiando solamente el nivel del nodo A,
en la Figura 15.14. Nótese que se preserva la propiedad de que el nodo que aumenta su nivel
tiene ambos hijos iguales y de un nivel menor.
t
n
a
i-1
i
t
A i
b
i-1
B
C i-1
i
D i-1
A i+1
n
a
i-1
i
B
b
i-1 C i-1
Figura 15.15. Inserción por la izquierda. Cambio de nivel.
Profesor Leopoldo Silva Bijit
20-01-2010
i
D i-1
Árboles AA.
9
b) B de nivel (i-1).
El nodo C debe tener nivel (i-2). D puede ser de nivel (i-1) o (i-2). Si A es hijo izquierdo, su
padre tiene nivel (i+1); y si es hijo derecho podría ser de nivel i.
t
a
A i
n
i
i-1
b
B
i-1
C i-2
i-1
D i-1
Figura 15.16. Inserción por la izquierda. B de nivel (i-1).
Luego del skew en t, el árbol es AA, y el diagrama se muestra en la Figura 15.17. Es preciso
continuar la revisión ascendente si A era un hijo derecho, ya que en este caso podrían producirse
tres nodos consecutivos de igual nivel.
t
n
a
i
i-1
A i
b
i-1
B
C i-2
i-1
D i-1
Figura 15.17. Inserción por la izquierda. Luego de skew en t.
15.2.4. Inserción por la derecha.
En este caso B debe ser de nivel (i-1). Si en el ascenso por el lado derecho, n incrementó su
nivel, debe cumplirse que sus hijos son de nivel (i-1). El árbol es AA, y no requiere
modificaciones. Debe continuarse la revisión ascendente si A es hijo derecho, ya que podrían
producirse tres nodos adyacentes de igual nivel.
t
A i
B
C i-2
i-1
D i-1 a
n
i
i-1
b
i-1
Figura 15.18. Inserción por la derecha. B de nivel i-1.
La operación torcer (skew) remueve los enlaces horizontales izquierdos (en el mismo nivel),
rotando en el padre a la derecha. No se propagan cambios hacia abajo, ya que se cambia un
horizontal izquierdo por un horizontal derecho.
Profesor Leopoldo Silva Bijit
20-01-2010
10
Estructuras de Datos y Algoritmos
Sin embargo la operación torcer (skew) puede crear dos enlaces horizontales derechos
consecutivos. La operación partir (split) remueve los dos rojos adyacentes mediante una
rotación izquierda y aumentando un nivel al padre.
Para mantener las propiedades de un árbol AA, es necesario balancear los nodos, que se
recorren al descender para insertar, en forma ascendente hasta la raíz.
Basta efectuar, de acuerdo al trabajo original, en cada nodo de la ruta ascendente:
t=skew(t);
t=split(t);
Sin embargo de acuerdo al análisis realizado, en cada nivel de recursión se efectúa un cambio de
nivel, o un skew o un split. Lo cual puede plantearse:
Si niveles de los hijos de t son iguales, aumentar el nivel de t.
Si son diferentes:
Si hijo izquierdo de t es de igual nivel que t: torcer
Si son diferentes:
Si nieto derecho de t es de igual nivel que t: partir.
El siguiente segmento explica las operaciones, que deben efectuarse en cada nodo de la ruta
ascendente, en términos de rotaciones. La rotación izquierda debe incorporar el cambio de nivel
de la nueva raíz.
if ((t->left->nivel== t->nivel ) && (t->right->nivel== t->nivel)) t->nivel++;
else if (t->left->nivel== t->nivel ) t=rrot(t);
else if (t->right->right->nivel== t->nivel ) t=lrot(t);
15.3. Análisis del descarte.
En el proceso de ajuste de niveles en el ascenso, se ha borrado una hoja en uno de los subárboles
de t, de nivel (i+1). El árbol cuya raíz es n, ya ha sido corregido y cumple las propiedades; así
también el árbol cuya raíz es B, ya que no ha sido modificado. Corresponde recuperar las
propiedades del árbol con raíz A, apuntado por t.
La Figura 15.19, a la izquierda, muestra los nodos involucrados en el análisis.
Si n es de nivel i, no es necesario seguir revisando en el ascenso. Solo es preciso corregir si
nivel de n es (i-1).
En el trabajo original se plantea, como ejercicio, que el peor caso de desbalance en el descarte
puede ser corregido por a lo más 3 skews y 2 splits. Es decir con:
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
11
if (ok && ((t->left->nivel < t->nivel-1) || (t->right->nivel < t->nivel-1)))
{ tnivel=t->nivel;
t->nivel = t->nivel -1;
if (t->right->nivel > t->nivel) t->right->nivel = t->nivel;
t=skew(t);
t->right=skew(t->right);
t->right->right=skew(t->right->right);
t=split(t);
t->right=split(t->right);
if (tnivel==t->nivel) ok=0;
}
Sin embargo el análisis de los diferentes casos resulta complejo como se verá a continuación.
15.3.1. Ascenso por la izquierda.
a1) B de nivel (i+1).
Esto implica que C y D deben ser de nivel i.
Se tienen 4 subcasos. E de nivel i o (i-1) y F de nivel i o (i-1).
a11) Con E y F de nivel i.
A la derecha de la Figura 19, se muestra luego del cambio de niveles de t y t->right. No se
requiere en este caso efectuar un skew en t.
t
A i+1
n
i-1
B
C
a
t
i+1
i
i-1
D
E
e
i-1
n
i-1
i
B
C
F
i
f
A i
i
a
i
i-1
i-1
i
D
E
e
i-1
i
F
i
f
i
i-1
Figura 15.19. Ascenso por la izquierda. E y F son de nivel i.
La Figura 15.20 a la izquierda muestra el diagrama luego del skew en t->right. A la derecha de
la Figura 15.20, se muestra luego del skew en t->right->right (el nieto de t).
Profesor Leopoldo Silva Bijit
20-01-2010
12
Estructuras de Datos y Algoritmos
t
A i
a
i-1
C
a
t
i
i-1
B
A i
n
i
i-1
C
i
E
E
i
D
i
a
B
i-1
e
e
i-1
f
i-1
F
i
i-1
f
i
i
D
i
i-1
F
i
Figura 15.20. Ascenso por la izquierda. Luego de tres operaciones torcer.
La Figura 15.21 a la izquierda muestra el diagrama luego del split en t. A la derecha de la Figura
15.21, se muestra luego del split en t->right.
t
t
C i+1
A i
n i-1
E
a
i-1
e
C
i+1
B
A i
i
B
i
i-1
n
D
f
i-1
a
i-1
E
i
e
i-1
f
i+1
D
i
i
i-1
F
i
i-1
F
i
Figura 15.21. Ascenso por la izquierda. Luego de las dos operaciones partir.
Como el nivel del nodo raíz no cambia, no sigue la revisión ascendente.
a12) Con E de nivel (i-1) y F de nivel i.
B de nivel (i+1) implica que C y D son de nivel i.
A la derecha de la Figura 15.22, se muestra luego del cambio de niveles de t y t->right. No se
requiere en este caso efectuar un skew en t.
t
A i+1
n
i-1
t
B
C
i+1
i
D
n
i-1
E
i-1
i
B
C
F
a
A i
i
i
D
i
i-1
i
F
a
i-1
E
i
i-1
Figura 15.22. Ascenso por la izquierda. Con E de nivel (i-1), y F de nivel i.
La Figura 15.23 muestra luego del skew en t->right.
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
13
t
A i
n
i-1
C
a
i
i-1
B
E
i
i-1
D
i
F
i
Figura 15.23. Ascenso por la izquierda. Con E de nivel (i-1), y F de nivel i.
No hay skew en t->right->right. La Figura 15.24 muestra luego del Split en t.
t
C
i+1
A i
n
i-1
B
a
i-1 E
i
i-1
D
i
F
i
Figura 15.24. Ascenso por la izquierda. Con E de nivel (i-1), y F de nivel i.
La Figura 15.24 muestra luego del split en t->right .
t
C
i+1
A i
n
i-1
a
i-1 B
E
D
i+1
i
F
i
i-1
Figura 15.24a. Ascenso por la izquierda. Con E de nivel (i-1), y F de nivel i.
No sigue revisión ascendente.
a13) Con E de nivel (i-1) y F de nivel ( i-1).
Similar al caso anterior, excepto que no se realiza el split en t->right, resulta la Figura 15.24b.
t
C
i+1
A i
n
i-1
B
a
i-1 E
i-1
i
D
i
F
i-1
Figura 15.24b. Ascenso por la izquierda. Con E de nivel (i-1), y F de nivel (i-1).
Profesor Leopoldo Silva Bijit
20-01-2010
14
Estructuras de Datos y Algoritmos
a14) Con E de nivel i y F de nivel ( i-1).
Se trata igual al caso a11).
a2) B de nivel i.
C debe ser (i-1). No importa nivel de E.
a21) Con D de nivel i.
A la derecha de la Figura 15.25, se muestra luego de cambio nivel sólo en A. No se efectúa el
skew en t ni en t->right, ni en t->right->right.
t
A i+1
n
i-1
t
B
i
C i-1
a
i-2
n
D
E
A i
i-1
B
i
i
C i-1
i-1
a
i-2
D
E
i
i-1
Figura 15.25. Ascenso por la izquierda. Con B de nivel i.
La Figura 15.26, muestra luego del split en A. No hay split en D.
t
B
i+1
A i
n
i-1
D
i
C i-1
a
i-2
E
i-1
Figura 15.26. Ascenso por la izquierda. Con B de nivel i.
No sigue revisión ascendente.
a22) Con D de nivel (i-1).
Si D es (i-1) no hay split en t, sólo cambia el nivel de A, y la revisión ascendente debe
continuar.
Pueden resumirse las acciones necesaria para balancear el árbol cuando se asciende por la
izquierda, con el siguiente segmento, que muestra las acciones en términos de rotaciones. Se
emplea la variable ok, para continuar o no la revisión de las propiedades en el ascenso.
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
15
//ascenso por la izquierda.
if(t->left->nivel< t->nivel-1)
{
if (t->right->nivel== t->nivel ) // Caso a1). B de nivel (i+1)
{ t->nivel--; t->right->nivel--; ok=0; //ok=0 implica no continuar revisión ascendente
t->right=rrot(t->right); t=lrot(t);
if (t->right->nivel==t->right->right->right->nivel) // F de nivel i.
{ if (t->right->left->nivel== t->right->nivel ) {t->right=rrot(t->right);} //a11
t->right=lrot(t->right); //a13
}
else if (t->right->left->nivel==t->right->nivel) t->right->nivel++; //a12
}
else //if (t->right->nivel==t->nivel-1) //Caso a2). B de nivel i.
{ t->nivel--;
if(t->right->right->nivel==t->nivel) {t=lrot(t); ok=0;} //a21
}
}
Lo cual muestra que en el peor caso se requieren 4 rotaciones para mantener las propiedades de
un árbol AA, en los nodos de la ruta ascendente. Pero el código es similar en complejidad a los
árboles coloreados.
15.3.2. Ascenso por la derecha.
B debe ser de nivel i y C de nivel (i-1).
b1) Con D de nivel i.
F debe ser de nivel (i-1). Luego de corregir nivel sólo en A se tiene el diagrama a la derecha de
la Figura 15.27.
t
t
A i+1
B
i
n
C i-1
D
b
i
n
C i-1
i-1
f
B
i-1
i
A i
F
i-1
i-2
a
D
b
i-1
i
i-1
f
Figura 15.27. Ascenso por la derecha. Con D de nivel i.
Luego del primer Skew en t, resulta la Figura 15.28.
Profesor Leopoldo Silva Bijit
20-01-2010
i-1
F
i-1
i-2
a
i-1
16
Estructuras de Datos y Algoritmos
t
B
i
C i-1
A i
D
b
n
i
i-1
f
F
i-1
i-2
a
i-1
i-1
Figura 15.28. Ascenso por la derecha. Con D de nivel i.
Luego del segundo skew en t->right, se tiene la Figura 15.29.
t
B
i
C i-1
D
b
i
i-1
A i
f
F
i-1
i-2
a
n
i-1
i-1
Figura 15.29. Ascenso por la derecha. Con B de nivel i.
El tercer skew en t->right->right no se realiza.
Luego del primer split en t, resulta la Figura 15.30.
t
D i+1
B
C i-1
i
b
A i
i-1
f
F
i-2
i-1
n
a
i-1
i-1
Figura 15.30. Ascenso por la derecha. Con B de nivel i.
El split en t->right no se realiza. No sigue revisión en ascenso
b2) Con D de nivel i-1.
B debe ser de nivel i y C debe ser de nivel (i-1). El nivel de F no importa.
La Figura 15.31 a la derecha muestra luego de la corrección del nivel de A.
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
17
t
t
A i+1
B
i
n
C i-1
b
i-2
B
i-1
D i-1
A i
i
n
C i-1
F
i-1
D i-1
i-1
b
i-2
F
i-1
Figura 15.31. Ascenso por la derecha. Con D de nivel i-1.
Luego del primer Skew en t, resulta La Figura 15.32.
t
B
i
C i-1
A i
n
D i-1
b
i-2
F
i-1
i-1
Figura 15.32. Ascenso por la derecha. Con D de nivel i-1.
No se realizan los skew en el hijo y en el nieto derecho de t. Tampoco se realizan los split.
El siguiente segmento ilustra las acciones para mantener las propiedades en caso de ascenso por
la derecha.
if (t->right->nivel < t->nivel-1) //ascenso por la derecha
{ t->nivel--; //se desciende el nivel
if (t->left->right->nivel == t->nivel) {t->left = lrot(t->left); ok=0;} //Caso b1).
t=rrot(t);
}
15.4. Centinelas y encabezados.
En aplicaciones con estructuras que tienen un inicio y un final, el diseño de las funciones
requiere un tratamiento especial en los bordes. Tradicionalmente puede uniformarse el
tratamiento al inicio introduciendo como primer elemento un nodo denominado encabezado o
header. Así también para finalizar la estructura puede agregarse un nodo denominado centinela
o fondo que facilite las operaciones en la base de la estructura.
Además la introducción de este nodo permite uniformar el tratamiento de funciones que operan
con los descendientes de un nodo, como es el caso de las operaciones skew y split en los árboles
AA.
Profesor Leopoldo Silva Bijit
20-01-2010
18
Estructuras de Datos y Algoritmos
Si se agrega un nodo al cual apuntan los descendientes de todas las hojas, se tiene la Figura
15.33. Nótese que los enlaces, izquierdo y derecho, del nodo centinela apuntan a sí mismo. De
este modo todos los nodos de los primeros niveles tienen descendientes bien definidos y no es
preciso establecer condicionales para construcciones como: p->right y p->right->right.
Si las hojas tuvieran enlaces izquierdos y derechos apuntando a NULL, antes de emplear en una
expresión p->right habría que asegurarse que p no apunte a NULL.
2
1
0
Figura 15.33. Nodo centinela. De nivel 0.
En otras aplicaciones los enlaces del centinela pueden apuntar al nodo raíz, logrando de este
modo listas circulares. Si los nodos tienen padre, el del centinela puede apuntar a la raíz o a
NULL dependiendo de la condición que se desee simplificar.
Veremos a continuación el uso clásico de un nodo centinela en una operación de búsqueda de un
valor en la estructura, cuyo resultado puede ser o no exitoso. Se carga en el nodo centinela el
valor que desea buscarse, de este modo se asegura una búsqueda exitosa. Discernir si el valor
estaba o no, consiste simplemente en determinar si se lo encontró o no en el nodo centinela.
El siguiente segmento ilustra el diseño, se ha supuesto un nodo centinela apuntado por una
variable externa a la función denominada nil.
//buscar con centinela
pnodo Buscar(data x, pnodo p)
{ if (p==nil) return NULL;
nil->clave=x; //carga valor en nodo centinela.
while ( p->clave != x) if (p->clave> x) p=p->left; else p=p->right;
if(p==nil) return (NULL); else return p;
}
15.5. Tipos de datos.
typedef int data;
typedef struct node {
struct node *left, *right;
int nivel;
data clave;
} nodo, *pnodo;
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
19
typedef pnodo arbol;
//Varibles globales
pnodo nil;
nodo centinela;
void initglobalvariables()
{ nil=&centinela;
nil->nivel = 0; //nivel del centinela, está bajo las hojas.
nil->left = nil;
nil->right = nil;
}
15.6. Creación de nodo.
La inserción se produce en las hojas, y siempre en nivel 1. Además el nuevo nodo tiene sus
descendientes apuntando al centinela.
pnodo getnodo(data valor)
{ pnodo p = (pnodo) malloc(sizeof(nodo));
if (p==NULL) {printf("Error memoria\n"); exit(1);}
else
{ p->clave = valor;
p->left = nil; //apuntan al centinela
p->right = nil;
p->nivel = 1; //hojas en nivel 1.
}
return(p);
}
15.7. Listador de la estructura.
Con fines de depurar las funciones, conviene disponer de una función que muestre en forma de
texto, los valores almacenados en el árbol.
Se efectúa un recorrido en orden, mostrando la clave y el nivel de cada nodo.
void prtnivel(pnodo p)
{ if (p!= nil)
{
prtnivel(p->left);
printf ("%d,%d ", p->clave, p->nivel);
prtnivel(p->right);
}
}
Profesor Leopoldo Silva Bijit
20-01-2010
20
Estructuras de Datos y Algoritmos
15.8. Operaciones básicas.
/* rotación derecha */
pnodo rrot(pnodo t)
{ register pnodo temp=t;
t = t->left;
temp->left = t->right;
t->right = temp;
return (t);
}
/* rotación izquierda */
pnodo lrot (pnodo t)
{ register pnodo temp=t;
t = t->right;
temp->right = t->left;
t->left = temp;
t->nivel++;
return(t);
}
pnodo skew (pnodo t)
{ pnodo temp;
if (t->left->nivel== t->nivel ) //no falla, en los niveles inferiores, debido al centinela
{ /* rotación derecha */
temp = t;
t = t->left;
temp->left = t->right;
t->right = temp;
}
return (t);
}
pnodo split (pnodo t)
{ pnodo temp;
if (t->right->right->nivel== t->nivel )
{ /* rotación izquierda */
temp = t;
t = t->right;
temp->right = t->left;
t->left = temp;
t->nivel = t->nivel +1;
}
return(t);
}
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
21
Para evitar la sobrecarga del llamado a funciones, las operaciones se pueden codificar
empleando macros. Debido a que son de varias líneas, se los suele definir empleando un lazo
while y el carácter de continuación de línea. En lugar de usar t=lrot(t); se escribe: lrotm(t);.
#define lrotm(t) do { \
{ temp=t;
\
t = t->right;
\
temp->right = t->left;\
t->left= temp;
\
t->nivel++;
\
}
\
} while(0)
15.9. Buscar.
El mismo creador de los árboles AA, plantea una forma original de efectuar una búsqueda en
árboles, empleando solamente una comparación. Para visualizar la diferencia se tiene la
búsqueda clásica con dos comparaciones y una asignación en el lazo.
pnodo Buscar2(data x, pnodo p)
{ if (p==nil) return NULL;
while ( p != nil)
{ if (p->clave>x) p=p->left;
else if (p->clave< x) p=p->right;
else return p; //lo encontró
}
return (NULL);
}
//primera comparación
//segunda comparación
La siguiente tiene una comparación y dos asignaciones en el peor caso, en cada pasada por el
lazo de repetición. Se emplea esta forma en la operación descarte.
pnodo Buscar1(data x, pnodo p)
{ pnodo t=p;
if (p==nil) return NULL;
while ( p != nil)
if (p->clave>x) p=p->left; else {t=p; p=p->right;}
if(t->clave==x) return t;
else return (NULL);
}
15.10. Insertar.
Diseño recursivo. Empleando rotaciones para mantener las propiedades de los árboles AA.
Profesor Leopoldo Silva Bijit
20-01-2010
22
Estructuras de Datos y Algoritmos
pnodo insertar(data x, pnodo t)
{
if (t == nil) {t=getnodo(x); ok=1;}
else {
if (x < t->clave) t->left=insertar(x, t->left);
else if (x> t->clave) t->right=insertar(x, t->right);
else ok=0; //si la clave ya estaba, no se inserta ni se revisan propiedades.
if (ok) //rebalancea si logró insertar
if ((t->left->nivel== t->nivel ) && (t->right->nivel== t->nivel)) {t->nivel++;}
else if (t->left->nivel== t->nivel ) t=rrot(t);
else if (t->right->right->nivel== t->nivel ) t=lrot(t);
}
return (t);
}
15.11. Descartar.
El diseño es más complejo y las operaciones para preservar las propiedades ocupan parte
importante del código; sin embargo son más sencillas que en el caso de árboles coloreados. Las
operaciones se han planteado en términos de rotaciones, en lugar de las de torcer y partir (skew
y split).
pnodo descartar(data x, pnodo t)
{ register pnodo p;
int tnivel;
//register pnodo temp;
if (t != nil)
{ /* 1: Desciende hasta el centinela, manteniendo punteros last y deleted. */
ok=0;
last = t; //last y deleted no son automáticas. Son globales.
if (x < t->clave) t->left=descartar(x, t->left);
else { deleted =t; t->right=descartar(x, t->right);
}
/* 2: Al llegar al centinela, last apunta a la hoja sucesora */
/* deleted apunta al que será descartado, si lo encontró. */
if (t ==last && (deleted != nil) && (x ==deleted->clave))
{ deleted->clave = last->clave; //reemplaza clave del sucesor
deleted = nil;
t=nil;
//t = t->right;
free (last); //libera hoja
ok=1;
}
/* 3: Luego del descarte, las invocaciones recursivas continúan aquí.*/
/* Se revisan los nodos por los cuales se descendió
*/
/* Inicialmente, t apunta al padre del que se descartó
*/
else
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
23
if (ok && ((t->left->nivel < t->nivel-1) || (t->right->nivel < t->nivel-1)))
{ //printf ("%d, %d \n", t->clave,t->nivel);//muestra ruta en ascenso
tnivel=t->nivel;
t->nivel = t->nivel -1; //se desciende el nivel
//también si tenía horizontal derecho
if (t->right->nivel > t->nivel) t->right->nivel = t->nivel;
if (t->left->nivel== t->nivel ) t=rrot(t); //rrotm(t);
// si queda un horizontal izquierdo
p=t->right;
if (p->left->nivel== p->nivel ) p=rrot(p); //rrotm(p);
// si queda un horizontal izquierdo del hermano derecho
p=p->right;
if (p->left->nivel== p->nivel ) p=rrot(p); //rrotm(p);
// si queda un horizontal izquierdo del nieto
//si se tiene el peor caso se requieren dos split
if (t->right->right->nivel== t->nivel ) t=lrot(t); //lrotm(t);
p=t->right;
if (p->right->right->nivel== p->nivel ) p=lrot(p); //lrotm(p);
if (tnivel==t->nivel) ok=0;
}
}
return (t);
}
15.12. Verificación de las propiedades.
La siguiente función recursiva, efectúa un recorrido en todos los nodos del árbol, revisando si se
cumplen las propiedades. Es útil en la verificación de las funciones.
void check(pnodo p)
{ int k, tipo;
if (p!= nil)
{
check(p->left);
k=0;
if (p->left->nivel== p->nivel ) {tipo=1; k++;} //no se permiten hijos izquierdos horizontales
if (p->right->right->nivel== p->nivel ){tipo=2;k++;}//no pueden existir dos rojos adyacentes
//Se pueden agregar algunos test para verificar la estructura
//las hojas tienen como descendiente al centinela
if ((p->nivel==1) && (p->left!=nil) ) {tipo=3;k++;}
if ((p->nivel==1) && (p->right->nivel==1)&& (p->right->right!=nil)) {tipo=4;k++;}
//hijo izquierdo debe tener nivel menor que su padre
if (p->left->nivel >= p->nivel ) {tipo=5;k++;}
Profesor Leopoldo Silva Bijit
20-01-2010
24
Estructuras de Datos y Algoritmos
//hijo derecho debe tener nivel menor o igual que su padre
if (p->right->nivel > p->nivel ) {tipo=6;k++;}
//nivel del nieto menor que el del abuelo
if (p->right->right->nivel >= p->nivel ){tipo=7;k++;}
//nodo de nivel mayor que uno debe tener dos hijos
if ( (p->nivel>1) && (p->left==nil) ) {tipo=8;k++;}
if ( (p->nivel>1) && (p->right==nil) ) {tipo=9;k++;}
//Condiciones en rebalance de la operacion descarte
if (p->left->nivel < p->nivel-1) {tipo=10;k++;}
if (p->right->nivel < p->nivel-1) {tipo=11;k++;}
if(k)
{printf("Error=%d %d \n",tipo, p->clave);
prtinorder(p); putchar('\n');
prtinorder(tree); putchar('\n');
prtnivel(tree); putchar('\n');
}
check(p->right);
}
}
15.13. Test de las funciones.
Pueden agregarse inserciones y descartes en órdenes crecientes y decrecientes, lo cual genera
cuatro segmentos de inserciones seguidas de descartes.
Se pueden contar mediante una variable global op, las operaciones realizadas. Agregando op++,
dentro de las funciones que se desee evaluar. La medición del tiempo permite comparar el uso
de macros o la declaración de variables de tipo registro.
#define N 79
arbol tree;
int main(void)
{ int i;
clock_t start, stop; //tipo definido en time.h
int totaltime = 0;
initglobalvariables();
tree=nil;
start = clock();
srand(1);
for(i=1;i<=N;i++)
{ tree=insertar(rand()%1023, tree);
check(tree);
//prtinorder(tree);putchar('\n');
}
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
25
for(i=1;i<=N;i++)
{ tree=descartar(tree->clave, tree);
check(tree);
//prtinorder(tree); putchar('\n');
}
stop = clock();
totaltime += (stop-start); // Mantiene el tiempo usado por la acción. Aproximadamente.
printf("Tiempo acumulado = %d [ticks]\n", totaltime);
printf("\nOp= %d \n", op);
printf("\nFin test \n");
return (0);
}
Referencias.
Arne Andersson. “Balanced Search Trees Made Simple”. Workshop on Algorithms and Data
Structures, pages 60-71. Springer Verlag, 1993.
A. Andersson. “A note on searching in a binary search tree”. Software-Practice and Experience,
21(10):1125 1128, 1991.
Profesor Leopoldo Silva Bijit
20-01-2010
26
Estructuras de Datos y Algoritmos
Índice general.
CAPÍTULO 15 ............................................................................................................................................1
ÁRBOLES AA. ...........................................................................................................................................1
15.1. PROPIEDADES DE LOS ÁRBOLES AA. ................................................................................................1
15.2. ANÁLISIS DE LA OPERACIÓN INSERCIÓN. ..........................................................................................2
15.2.1. Ejemplos de inserción. .............................................................................................................5
15.2.2. Diseño de las operaciones skew y split. ...................................................................................7
15.2.3. Inserción por la izquierda. .......................................................................................................8
a) B de nivel i. .................................................................................................................................................. 8
b) B de nivel (i-1). ............................................................................................................................................ 9
15.2.4. Inserción por la derecha. .........................................................................................................9
15.3. ANÁLISIS DEL DESCARTE. ...............................................................................................................10
15.3.1. Ascenso por la izquierda. .......................................................................................................11
a1) B de nivel (i+1). ....................................................................................................................................... 11
a11) Con E y F de nivel i.......................................................................................................................... 11
a12) Con E de nivel (i-1) y F de nivel i. .................................................................................................... 12
a13) Con E de nivel (i-1) y F de nivel ( i-1). ............................................................................................. 13
a14) Con E de nivel i y F de nivel ( i-1). .................................................................................................. 14
a2) B de nivel i. .............................................................................................................................................. 14
a21) Con D de nivel i. ............................................................................................................................... 14
a22) Con D de nivel (i-1). ......................................................................................................................... 14
15.3.2. Ascenso por la derecha. .........................................................................................................15
b1) Con D de nivel i. ...................................................................................................................................... 15
b2) Con D de nivel i-1.................................................................................................................................... 16
15.4. CENTINELAS Y ENCABEZADOS. .......................................................................................................17
15.5. TIPOS DE DATOS. ............................................................................................................................18
15.6. CREACIÓN DE NODO. ......................................................................................................................19
15.7. LISTADOR DE LA ESTRUCTURA. ......................................................................................................19
15.8. OPERACIONES BÁSICAS. .................................................................................................................20
15.9. BUSCAR. .........................................................................................................................................21
15.10. INSERTAR. ....................................................................................................................................21
15.11. DESCARTAR..................................................................................................................................22
15.12. VERIFICACIÓN DE LAS PROPIEDADES. ...........................................................................................23
15.13. TEST DE LAS FUNCIONES. .............................................................................................................24
REFERENCIAS. .........................................................................................................................................25
ÍNDICE GENERAL. ....................................................................................................................................26
ÍNDICE DE FIGURAS. ................................................................................................................................27
Profesor Leopoldo Silva Bijit
20-01-2010
Árboles AA.
27
Índice de figuras.
FIGURA 15.1. ÁRBOLES AA, DE HASTA 3 NODOS. ......................................................................................... 1
FIGURA 15.2. INSERCIÓN POR LA IZQUIERDA. SKEW. .................................................................................... 2
FIGURA 15.3. INSERCIÓN POR LA IZQUIERDA. SKEW Y SPLIT EN EL MISMO NIVEL. ........................................ 3
FIGURA 15.4. INSERCIÓN POR LA IZQUIERDA. SKEW Y SPLIT EN NIVELES DE RECURSIÓN DIFERENTES. ......... 3
FIGURA 15.5. INSERCIÓN POR LA DERECHA................................................................................................... 4
FIGURA 15.6. FORMAS DE ÁRBOLES AA PARA 4, 5, 6 Y 7 NODOS. ................................................................. 4
FIGURA 15.7. INSERCIÓN DE NODO CON VALOR 15 EN ÁRBOL AA................................................................ 5
FIGURA 15.8. LUEGO DE SPLIT EN NODO CON CLAVE 13. .............................................................................. 5
FIGURA 15.9. LUEGO DE SPLIT EN NODO CON CLAVE 10. .............................................................................. 6
FIGURA 15.10. LUEGO DE SPLIT EN NODO CON CLAVE 4. .............................................................................. 6
FIGURA 15.11. LUEGO DE INSERTAR EL 8, Y LUEGO DE SKEW EN 9 Y ASCENDER HASTA LA RAÍZ. ................. 6
FIGURA 15.12. LUEGO DE INSERTAR EL NODO CON VALOR 7 Y LUEGO DEL SKEW EN 8. ................................ 7
FIGURA 15.13. LUEGO DE SPLIT EN 7, Y LUEGO DEL SKEW EN 10. ................................................................. 7
FIGURA 15.14. INSERCIÓN POR LA IZQUIERDA. B DE NIVEL I. ........................................................................ 8
FIGURA 15.15. INSERCIÓN POR LA IZQUIERDA. CAMBIO DE NIVEL. ............................................................... 8
FIGURA 15.16. INSERCIÓN POR LA IZQUIERDA. B DE NIVEL (I-1). .................................................................. 9
FIGURA 15.17. INSERCIÓN POR LA IZQUIERDA. LUEGO DE SKEW EN T. .......................................................... 9
FIGURA 15.18. INSERCIÓN POR LA DERECHA. B DE NIVEL I-1. ....................................................................... 9
FIGURA 15.19. ASCENSO POR LA IZQUIERDA. E Y F SON DE NIVEL I. ........................................................... 11
FIGURA 15.20. ASCENSO POR LA IZQUIERDA. LUEGO DE TRES OPERACIONES TORCER. ............................... 12
FIGURA 15.21. ASCENSO POR LA IZQUIERDA. LUEGO DE LAS DOS OPERACIONES PARTIR. ........................... 12
FIGURA 15.22. ASCENSO POR LA IZQUIERDA. CON E DE NIVEL (I-1), Y F DE NIVEL I. .................................. 12
FIGURA 15.23. ASCENSO POR LA IZQUIERDA. CON E DE NIVEL (I-1), Y F DE NIVEL I. .................................. 13
FIGURA 15.24. ASCENSO POR LA IZQUIERDA. CON E DE NIVEL (I-1), Y F DE NIVEL I. .................................. 13
FIGURA 15.24A. ASCENSO POR LA IZQUIERDA. CON E DE NIVEL (I-1), Y F DE NIVEL I................................. 13
FIGURA 15.24B. ASCENSO POR LA IZQUIERDA. CON E DE NIVEL (I-1), Y F DE NIVEL (I-1). .......................... 13
FIGURA 15.25. ASCENSO POR LA IZQUIERDA. CON B DE NIVEL I. ................................................................ 14
FIGURA 15.26. ASCENSO POR LA IZQUIERDA. CON B DE NIVEL I. ................................................................ 14
FIGURA 15.27. ASCENSO POR LA DERECHA. CON D DE NIVEL I. .................................................................. 15
FIGURA 15.28. ASCENSO POR LA DERECHA. CON D DE NIVEL I. .................................................................. 16
FIGURA 15.29. ASCENSO POR LA DERECHA. CON B DE NIVEL I. .................................................................. 16
FIGURA 15.30. ASCENSO POR LA DERECHA. CON B DE NIVEL I. .................................................................. 16
FIGURA 15.31. ASCENSO POR LA DERECHA. CON D DE NIVEL I-1................................................................ 17
FIGURA 15.32. ASCENSO POR LA DERECHA. CON D DE NIVEL I-1................................................................ 17
FIGURA 15.33. NODO CENTINELA. DE NIVEL 0............................................................................................ 18
Profesor Leopoldo Silva Bijit
20-01-2010