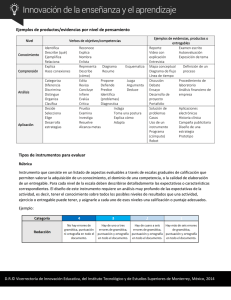
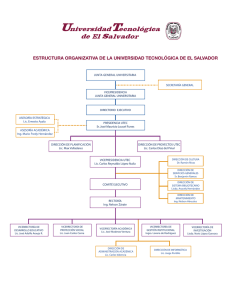
temario del diplomado de matematicas

Módulo introductorio
Presentación
La enseñanza de las matemáticas no sólo se cubre en el aula de una escuela, a lo largo
de los años, maestros, artistas, cantantes, padres de familia lo han hecho a través de
diversos medios.
Es así como el Conde Contar enseña a los pequeños a contar al derecho y al revés,
mientras los niños ven el televisor; Dan Brown, autor del best seller Código Da Vinci,
enseña matemáticas dando una descripción de una de las salas del Museo del Louvre
detallando la forma geométrica de su piso; y los artistas enseñan matemáticas como los
españoles Enrique y Ana quienes en los años 80’s enseñaron a niños hispanoparlantes a
multiplicar hasta la tabla del 12 por medio de sus canciones.
Hoy en día, se aplican las matemáticas al:
…es decir, las matemáticas están en todo. Todos las usamos a diario, consciente o
inconscientemente. Así hayamos sido buenos o malos alumnos de matemáticas, todos
vivimos con ellas.
Pero entonces:
¿Por qué, si se convive a diario con ellas, existen tan bajos
resultados en pruebas reconocidas por organismos mundiales?
¿Por qué, si se convive a diario con ellas, existen tan bajos resultados en pruebas
reconocidas por organismos mundiales?
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Pruebas como PISA (de su acrónimo en inglés: Programme for International Student
Assessment, que en español significa Proyecto Internacional para la Evaluación de
Alumnos) auspiciada por la Organización para la Cooperación y Desarrollo Económico
(OCDE) y la Organización de las Naciones Unidas (ONU) ofrecen una visión sobre la
situación de los estudiantes en México en relación con estudiantes del resto del mundo.
Esta prueba evaluó en el año 2003 el desempeño de estudiantes que viven en 41
diferentes países del mundo, en las áreas de lectura, matemáticas y ciencias.
Esta evaluación se aplica a jóvenes de 15 años tomando una muestra de 4 mil 500 a 10
mil alumnos. México se encuentra en el lugar 35 muy por debajo de la media propuesta
por la OCDE que es de 500 puntos.
¿Cuál es el reto que enfrenta el profesor de hoy?
¿Qué es lo que más le preocupa al maestro del aula?
No sólo le preocupa que su alumno apruebe la materia de matemáticas, además quiere
formar a un individuo capaz de resolver problemas en su vida diaria. Un alumno que
cuando planee la fiesta de generación sepa graduarse sin poner dinero de su bolsa; que
cuando sepa la distancia en kilómetros de su ciudad natal a la playa más cercana, pueda
calcular las horas manejando para llegar sano y salvo a su destino.
El reto del maestro de matemáticas es formar un alumno que vea soluciones donde otros
ven problemas. Si el alumno se reconoce con habilidades para resolver problemas
cotidianos, probablemente será capaz de desenvolverse adecuadamente en el mundo tan
competitivo en el que le tocará vivir.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Tema 1. Estrategias para la enseñanza de las matemáticas
El concepto “estrategias” en el ámbito educativo, son todos los procedimientos y
herramientas que el profesor pone en marcha para que el alumno concrete las
propuestas establecidas en los objetivos de aprendizaje de un programa académico.
Por lo tanto, las estrategias están integradas en el propio proceso de enseñanza
aprendizaje; de ahí, que no deban trabajarse al margen del currículum.
Las estrategias las emplea el profesor al enseñar y el alumno al aprender y, si realmente
están bien diseñadas, las que se utilizan para transmitir la información y las que utilizan
los estudiantes para procesarla deben ser las mismas.
Ahora bien, las estrategias que deben plantearse para lograr el objetivo del aprendizaje
no son solamente de tipo cognitivo.
Por ejemplo: un alumno modelo puede tener una excelente comprensión,
pero si no atiende y controla su aprendizaje e incluso, si no logra concretarlo
para su posterior aplicación, esta capacidad de comprensión le sirve de poco.
Existen, por tanto, otros elementos que impactan en el rendimiento académico que son
muy importantes, como por ejemplo el atender y regular los propios procesos de
aprendizaje.
En este sentido, cuando un alumno puede
atender, entender y autorregular su
aprendizaje, su motivación aumenta y la
percepción de sí mismo y su autoconcepto se
vuelven más positivos.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Las estrategias bien diseñadas, evaluadas e implementadas, llevan de la mano al
profesor para el diseño de un plan de acción encaminado al logro de una meta, y en ese
camino como ganancia secundaria, se logra un cambio en el plano emocional del
alumno, lo que trae una predisposición favorable en él, facilitando el proceso de
enseñanza-aprendizaje.
En el modelo constructivista se privilegian acciones encaminadas a la construcción de
nuevos conocimientos. La meta es crear condiciones (desde motivacionales hasta
cognitivas) para que este aprendizaje constructivo ocurra.
En un ambiente diseñado para tal propósito:
De esta manera el aprendizaje está situado y se vería reforzado por la pertinencia de las
actividades, las cuales estarán determinadas a su vez por el carácter de las herramientas
que se tengan disponibles.
El proceso enseñanza-aprendizaje requiere de ejercicios independientes y variados,
con una complejidad que va en ascenso: empezar por lo fácil o sencillo hasta llegar a
lo más complejo buscando con este procedimiento que el estudiante logre entrelazar los
conocimientos adquiridos y luego se apropie de ellos, los procese, los transforme y los
aplique.
Esta estrategia (ir de lo simple a lo complejo) para lograr un aprendizaje significativo
se caracteriza porque requiere el constante desarrollo de la independencia del
pensamiento del estudiante.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Otra estrategia útil es el estudio dirigido, que es considerado una tarea que se apoya en
el interés del estudiante.
Es eficaz para realizar:
•
•
•
Investigaciones
Observaciones
Experimentos
•
•
•
Entrevistas
Búsqueda de datos y
Otros tipos de trabajos
individuales
El estudio dirigido permite desarrollar una serie de actividades orientadas hacia la
estimulación del estudiante en el campo productivo y el desarrollo del pensamiento
lógico, reflexivo y creativo.
Estudio
dirigido
Es un conjunto de
estrategias especializadas
que abarca una serie de
pasos lógicos para
Que el alumno adquiera
conocimientos y habilidades
Que el alumno solucione
problemas
Por eso, los métodos fundamentales de la educación deben ser aquéllos que induzcan a
la investigación, llámese práctica, estudio independiente de proyectos o como sea; lo
importante es que el estudiante tenga contacto directo con la realidad circundante o con
su entorno social.
Las estrategias para una enseñanza efectiva de las matemáticas deben involucrar
acciones a realizar fuera de la escuela, además de las internas.
Diferentes autores como Brilliant-Mills, Cobb, Bauersfeld, Word, Yackel, Pimm,
Rivière, coinciden en señalar que el conocimiento matemático se originó con intereses
prácticos, basta recordar que la matemática permite establecer relaciones entre los
objetos, sugeridas muchas veces por el mundo material y los objetos físicos.
Por tanto, un aspecto relevante en el diseño y la implementación de estrategias debe ser
la inclusión de aspectos cotidianos que permitan al estudiante relacionar lo aprendido en
un contexto de la vida real.
Después de esta pequeña introducción sobre las estrategias para enseñar matemáticas,
veamos a continuación cómo se puede adquirir el conocimiento matemático.
La adquisición del conocimiento matemático
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Al ser una ciencia exacta y abstracta, es importante reconocer que los conceptos
matemáticos no están contenidos en los objetos, sino que se refieren a ellos.
Esta complejidad debe llevar al profesor de matemáticas a considerar hasta qué grado la
matemática debe ser enseñada exclusivamente como una forma de conocimiento
abstracto, que se soporta a sí misma en conceptos y lenguajes más formales, estos
permiten su expresión y sirven como traductores para expresar más objetivamente sus
proposiciones y conceptos.
Tradicionalmente, quienes se han ocupado de la enseñanza de la matemática han
insistido también en la idea de que el conocimiento matemático debe ser reconstruido
por el estudiante pieza a pieza, de forma significativa sobre la base de experiencias
anteriores y de concepciones que son fundamentalmente contextuales.
Al tratar de unir esta doble línea de trabajo, Leino (1990) presupone que existen dos
procesos de construcción de la matemática cuando éstos se llevan a cabo en el contexto
escolar:
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
A su juicio, el único modo de que los alumnos aprendan matemáticas es que
reconstruyan los conceptos básicos de la matemática de un modo significativo.
Desde esta perspectiva, el objetivo sería proporcionar contextos adecuados para que se
produzca esa “matematización”, algo que supone alejarse de una perspectiva que
considera los conceptos de la matemática como algo ya hecho.
De acuerdo con Von-Glaserfeld (1987), los conceptos matemáticos han de ser
construidos de forma individual utilizando como base las concepciones propias del
alumno basadas en su conocimiento previo. A lo largo del proceso, los conflictos
cognitivos adoptan un papel preponderante para la creación de desequilibrios que
resultan ser, de acuerdo con Piaget (1974) uno de los mecanismos más relevantes para
la construcción cognitiva.
Referido todo ello al terreno de la enseñanza y aprendizaje de la matemática se advierte
pronto el papel protagónico del error. El error forma parte del aprendizaje, ya que indica
el grado de acercamiento al conocimiento. “No se trata de cómo corregir los
errores......sino considerarlos motor de debate y avance para todos” (Broitman,
Itzcovich; 2001).
La comparación entre procedimientos y el análisis acerca de los errores en la resolución
de un problema, les permitirá a los alumnos, avanzar en la comprensión de los
enunciados y en las estrategias de resolución. Hay que procurar que las consecuencias
de un error, producido por un alumno, sean las que se lo revelen; si tiene que ver que el
resultado es “absurdo” o es incorrecto, entonces, así comprenderá claramente que sus
procedimientos no eran buenos.
Muchas veces los alumnos siguen reglas erróneas, no siempre fáciles de entender para el
adulto que supervisa la resolución de un problema matemático o enseña a lograr la
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
solución; es importante tener en cuenta que las respuestas correctas pueden generarse a
partir de estas reglas, y por tanto resulta preponderante establecer un proceso de
comunicación efectivo para lograr un entendimiento cabal del proceso.
Para saber más sobre este tema, consulte el documento que se encuentra en la sección
del material de apoyo del módulo.
Cómo aprovechar el error para
enseñar y aprender
“La educación matemática debe centrarse en el desarrollo del “poder matemático”, lo
que significa el desarrollo de habilidades relacionadas con los siguientes aspectos: la
comprensión de conceptos y métodos matemáticos, el descubrimiento de relaciones
matemáticas, el razonamiento lógico y la aplicación de concepto, métodos y relaciones
matemáticas para resolver una variedad de problemas no rutinarios” (Schoenfeld, 1989,
p. 86).
Es difícil negar lo que Schoenfeld afirma en la cita anterior, pero resulta mucho más
complejo delimitar las vías concretas a través de las cuales puede lograrse la meta.
En este sentido la pregunta sería:
¿Cómo hacer posible que en el aula se pueda
encontrar el descubrimiento
del razonamiento matemático?
Específicamente sí se tiene la noción de que no existe una receta para lograrlo, debido a
que no existe solamente una forma de pensar matemáticamente, lo cual se ve apoyado
por los conceptos derivados de la teoría de estilos de aprendizaje.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
En suma, todo esto nos sugiere que el profesor debe combinar diversas estrategias
didácticas aplicadas a fomentar el pensamiento matemático, tratando de unir, por una
parte, las peculiaridades de esta forma de conocimiento que caracterizan el trabajo de
los profesionales en este campo y, por otro lado, su valor funcional fuera de las aulas.
Tema 2. Desarrollo de la intuición didáctica
La libertad de la enseñanza en la docencia, como muchas otras cosas en la vida,
depende de muchas cosas. Por lo general, la mayor parte de los docentes se ven
obligados a cumplir un determinado programa académico, el cual ha sido diseñado para
cumplir cierto número de temas, enseñar ciertos conocimientos o desarrollar habilidades
especificas; todo esto puede variar de una institución a otra.
Sin embargo, es posible “jugar” con estos programas y adaptarlos a la forma de trabajo
de cada docente.
La libertad que tiene el maestro dentro de su clase, siendo ésta bien entendida, permite
la creatividad y la implementación de estrategias para la enseñanza, en términos de la
selección de varios temas a ser tratados y que por su propia naturaleza (interés,
importancia o actualidad) puedan ser incluidos con el propósito de motivar e incentivar
a los estudiantes a mantenerse al día, o bien, con la finalidad de esclarecer dudas
durante la explicación de un tema difícil. En este sentido, la selección adecuada del
material expuesto a los alumnos es de vital importancia.
La percepción del estudiante hacia el docente cambia en la medida en que éste muestre
disposición a utilizar estrategias alternas para motivar y facilitar el aprendizaje. Es así
que la verdadera creatividad por parte del profesor consiste en su capacidad de aplicar
su intuición adecuadamente al contexto en el que se lleva a cabo la clase.
Desgraciadamente, no existe una fórmula para hacerlo.
De acuerdo con Jung (1981), la intuición es una función de percepción que incluye
factores subliminales, esto es, la posible relación de objetos aparentemente
desconectados en el campo de visión. Por su parte, Vaugham (1979) describe la
intuición como la incapacidad de poder explicar el por qué se sabe lo que se sabe (sic).
De esta manera:
•
•
•
•
•
El simple hecho de hacer conciente la dinámica en la que interactúa el grupo;
Percatarse de las acciones que tienden a ayudar a crecer a los alumnos;
Vislumbrar la mejor alternativa metodológica;
Advertir si algún alumno pasa por circunstancias adversas que se interpongan
en su desarrollo académico, y sobre todo;
Discernir lo que personalmente le sucede en la interacción educativa…
…son asuntos que no están descritos en ninguna guía o manual y mucho menos son
obtenidos de un curso explícito.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Por el contrario, son menesteres que se deben aprender de manera cotidiana, durante la
práctica y de manera personal e intransferible. Esa certeza que no puede explicarse
mediante la razón, que implica el conocimiento exacto de una cosa que comúnmente
llamamos intuición, puede ser lo suficientemente fuerte como para ser el detonador que
impulse una acción concreta.
Precisamente en esa naturaleza inexacta, irracional e inexplicable estriba tanto la
genialidad como el riesgo a correr más grande al aplicar la intuición al quehacer
educativo.
Se puede decir que la intuición educativa está conformada por una mezcla no siempre
bien proporcionada de sentido común, que es la experiencia acumulada del profesor y el
conocimiento de la realidad.
Pérez (2002) enuncia una serie de factores que en conjunto caracterizan a una persona
que utiliza la intuición con fines didácticos:
1. Reflexiona permanente
Este factor implica la observación contemplativa de todo lo que nos rodea, con la
finalidad de utilizar estos recursos en la práctica educativa.
2. Formula preguntas
En este apartado, la pregunta estrella sería ¿Qué pasaría si? Si bien esta pregunta podría
considerarse angular, lo más fascinante del asunto es que a su vez, desencadena una
serie de preguntas más, todas ellas dirigidas al objetivo primordial de aplicarlas en la
práctica.
3. Busca la innovación
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Puesto que los educandos de un curso no son los mismos de otros cursos, el contexto
sociocultural e institucional va modificándose con el tiempo, los contenidos temáticos
van enriqueciéndose con nuevas investigaciones o análisis, y uno mismo como
educador va evolucionando como persona; las propuestas formativas no pueden
permanecer estáticas. Es necesario adaptarlas, enriquecerlas, transformarlas
permanentemente.
Es aquí donde el profesor intuitivo entra en escena reformulando como si fuera la
primera vez que se preparara, utilizando otros puntos de partida, incorporando
elementos proporcionados por otros colegas o utilizando métodos que incluso pueden
romper percepciones, conceptos y esquemas obsoletos o carentes de significado.
4. Sistematización permanente
Los congresos, cursos, foros, paneles, entre otros, deben de ser vistos por los
académicos como semilleros de ideas más que como recetarios para lograr el éxito. En
este sentido, la sistematización debe enfocarse en el apropiamiento de las ideas con la
finalidad de mejorarlas, adaptarlas y reproducirlas con un sello particular.
5. Reflexiona la teoría
Al registrar, reflexionar, cuestionarse o sistematizar van surgiendo inquietudes que
hacen sentir la inminente necesidad de acudir a los libros, al Internet, a las revistas
especializadas... a comprender de forma más teórica lo que empíricamente se ha
vislumbrado como importante. En este sentido, la literatura especializada es también
una fuente inagotable de nuevas propuestas. Y no está por demás decir la necesidad de
divulgar los resultados obtenidos, es la clave para trascender.
Creatividad en la metodología
Ahora bien, la creatividad en la metodología del proceso enseñanza aprendizaje tiene
distintas vertientes.
Con la finalidad de hacer referencia a ellas, resulta conveniente el auxilio de una
analogía en la que se simulará el diseño, la implementación y la evaluación de un curso
como el viaje que realizará el profesor y sus alumnos, quienes serán el guía y los
viajeros respectivamente. Llegar al destino final del viaje será el equivalente a cumplir
con los objetivos del curso.
La creatividad con la que se manejen los obstáculos que tiene el viaje serán las
estrategias creativas con las cuales puede trabajar el guía. Veamos cómo se desarrolla
este viaje.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Para el guía de la expedición es importante
conocer las características de los
viajeros, para el caso de una clase, sería el
bagaje previo en términos de
conocimientos que poseen los alumnos, es
decir, el punto de partida. En este rubro,
resulta importante enfatizar que es
necesario que el docente sepa cuál es la
situación real en la que se encuentra el
estudiante y no en la que debería estar.
Después de conocer las características de los viajeros,
el guía enfrenta el desafío de diseñar una ruta
depurada que permita el paso libre de los viajeros,
cada uno de ellos con antecedentes y capacidades
diferentes. Quizá algunos de los viajeros requieran un
entrenamiento previo para poder resistir las
inclemencias del viaje, será labor del guía poner
especial cuidado en estos viajeros y al mismo tiempo
no retardar a los que ya están preparados. En el punto
de partida puede resultar estimulante para los viajeros
capacitados el acondicionar a los que no lo están. En
términos de estrategias, una opción sería la implementación de una buena dinámica
grupal que involucre la formación de equipos colaborativos, en la cual los líderes más
capacitados se responsabilicen, bajo la supervisión del guía para el acondicionamiento
intelectual de su patrulla de viaje.
Resulta deseable establecer una cantidad suficiente de
estaciones intermedias o metas parciales que representen un
efectivo avance para los viajeros, en el entendimiento de que
estas estaciones intermedias deben conducir un camino
directo hacia el destino final. Muchas veces, son necesarios
desvíos ocasionales alrededor de las estaciones intermedias y
estos pueden ser incluso recomendables o ilustrativos para
enriquecer con ejemplos o aplicaciones que a la larga pueden
ayudar al cumplimiento de la meta.
Durante el camino, el guía tiene en sus manos un arsenal de recursos que pueden ayudar
creativamente al cumplimiento de la meta. ¿Qué tal caería para un viajero una
refrescante bebida durante un trayecto caluroso? El salpicar cada una de las estaciones
intermedias con ejemplos extraídos de la realidad, facilita en gran medida la
comprensión del viaje ya que refrescan y reaniman para seguir adelante.
Retomando el contexto educativo, otro recurso podría ser el uso de analogías y juegos
pertinentes para cada grado escolar. Estas simples estrategias “visten” de innovación un
tema que puede resultar álgido o difícil de comprender y de explicar.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
¿Qué reacción tendrían los estudiantes de un curso de
probabilidad y estadística si el profesor inicia su clase planteando
las posibilidades que tiene un bateador de los Dodgers de los
Ángeles de ganar el premio al mejor bateador del año,
basándonos en las estadísticas de su desempeño durante la
temporada?
Seguramente será más fácil de entender el concepto de probabilidad en esos términos
que usando un ejemplo que tenga que ver con largas listas de probabilidades descritas
en un libro de texto. Para este mismo ejemplo:
¿Por qué no mostrar una parte del último juego en el que
participó el bateador, en el que la pantalla muestra sus
estadísticas en un recuadro y aplicar estos conocimientos
estableciendo una predicción?
Cada una de las estaciones en las que se hace un descanso para reforzar el
entendimiento de un tema debe de servir como detonador para cobrar nuevas fuerzas,
con la finalidad de alcanzar el objetivo trazado en el inicio. La capacidad del profesor
para lograr la variedad en una clase y estimular al estudiante (tratando de abarcar la
totalidad de estilos de aprendizaje y personalidades), será el punto de fusión de cada
estación recorrida hasta lograr completar el viaje, con la totalidad de los viajeros que
iniciaron la jornada, tal vez el guía y los viajeros terminarán extenuados pero contentos
y satisfechos por los logros obtenidos.
Es lógico pensar que en términos de aprendizaje es imposible evadir el tema de la
evaluación. Una excelente forma de asegurar que los contenidos van siendo asimilados
por los estudiantes es programar evaluaciones de medio término, para tener una prueba
más objetiva del avance, en aras de conocer el estatus parcial de los estudiantes.
Resultaría divertido hacer esta evaluación no con los trillados y nada didácticos
exámenes sorpresa, sino con un concurso que estimule el trabajo en equipo.
Algunos ejemplos pueden ser:
•
•
Realizar una olimpiada de conocimientos la última semana de clases.
o Los alumnos pueden ser organizados por filas, equipos, patrullas de
viaje.
o Se puede utilizar un tablero del popular juego de mesa Maratón® o
colocando globos inflados en el pizarrón con preguntas que deberán ser
contestadas por un miembro del equipo.
Realizar un rally de pistas en Internet.
¿Cuál es el límite? El que su propia creatividad le dicte.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
La enseñanza creativa y la implementación de estrategias didácticas sin duda serán
mucho más sencillas para el docente que es educador las 24 horas del día. Es decir,
aquel docente con pensamiento didáctico que aprovecha todos los estímulos a los que
está expuesto durante el día para aplicarlos en sus clases. Las ideas pueden provenir de
los anuncios publicitarios, series televisivas de moda y de una manera más formal, del
intercambio de ideas y sugerencias con jefes y subalternos.
El hecho de poder aterrizar las ideas y adaptarlas a los contenidos de un curso de
matemáticas para aplicarlas efectivamente en el salón de clases, es una de las claves
que distinguen al profesor creativo.
La intuición educativa, como ya se vio anteriormente, es entendida como la capacidad
de poder vislumbrar la posible aplicación de una idea obtenida de cualquier fuente
pertinente, pero no se puede comprar en ningún lado, es por eso que cada docente debe
llevar un registro de las ideas que vayan surgiendo e implementando, documentando si
el recurso utilizado funciona o no, para futura referencia.
De esta manera, al paso del tiempo se contará con una serie de estrategias que pueden
ser retomadas y adaptadas para cada situación particular.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Tema 3. El arte de la enseñanza efectiva
Existe la tendencia tradicional de ver el acto pedagógico bajo un sencillo esquema
lineal:
Se cree que este esquema se resume en el hecho de que un profesor enseña ciertos
conocimientos y que estos son aprendidos por el alumno. Y se utiliza aquí el término
conocimientos en un sentido muy amplio que comprende no sólo los conocimientos
teóricos que enseña un profesor, sino también las habilidades prácticas, los valores
éticos, los hábitos culturales y las muchas otras cosas que enseña.
La parte negativa del esquema lineal es que pone al profesor y al alumno en los
extremos de una línea y los sitúa por lo tanto a una cierta distancia. Además crea la idea
de que su relación está mediatizada por los conocimientos. Sin embargo esto no es del
todo cierto, al menos en el caso de la educación presencial.
En el acto pedagógico existe una relación directa entre el profesor y el estudiante, una
relación interpersonal. Por ello, es deseable ver el acto pedagógico bajo un esquema
distinto que tiene forma triangular:
Los tres elementos señalados -profesor, conocimientos, alumno- están relacionados más
equilibradamente y donde la relación profesor- alumno se manifiesta de una manera más
clara, recíproca e interactiva, además cada factor depende del otro para gestar el
aprendizaje.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
¿Por qué aprender a enseñar matemáticas?
La enseñanza de las matemáticas siempre ha sido un tema de debates y propuestas, por
un lado hay quienes defienden la enseñanza tradicional y por otro hay quienes apuestan
por un modelo educativo moderno. Sin embargo, bajo un esquema tradicional o
moderno, la problemática del fracaso escolar en el área sigue siendo latente, al menos
en los países latinoamericanos, evidencia de ello han sido los resultados en las últimas
pruebas internacionales.
El objetivo de estos exámenes internacionales ha sido reunir pruebas sobre los valores
personales y sociales, que son contenidos explícitos en la mayoría del currículo de los
países involucrados. Ejemplos de estos exámenes son:
Auspiciado por
OCDE (Organización para la cooperación y
desarrollo económico)
ONU (Organización de las Naciones
Unidas)
UNESCO (Organización de las naciones
unidas para la educación, ciencia y cultura).
Las áreas que se evalúan en ambos son la lectura, ciencias y matemáticas. Aunque nos
interesa ahondar más en el examen PISA a continuación se explican algunos resultados
y conclusiones importantes.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Las pruebas PISA
Las pruebas PISA tienen como objetivo:
Evaluar las destrezas y habilidades de los estudiantes para la vida adulta.
Considera tres áreas importantes:
Para PISA, la formación
matemática consiste en la
capacidad de identificar,
comprender e implicarse
en las matemáticas y
emitir juicios con
fundamento como
elemento necesario para
la vida privada, laboral y
social, actual y futura.
El estudio de PISA se aplica a jóvenes de 15 años. Cada país participante toma una
muestra de 4 mil 500 a 10 mil alumnos, los cuales además de resolver el examen
responden a cuestionarios sobre el medio socioeconómico del cual proceden. En la
Prueba PISA 2003 participaron 41 países, de los cuales Argentina, Brasil, Chile,
México y Perú corresponden a la representación latinoamericana.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
PISA no es una evaluación de la efectividad de las escuelas de un país, sino de los
niveles de aprendizaje de sus jóvenes de 15 años, resultado tanto de la escuela como de
las influencias familiares y sociales. Los resultados de PISA, por consiguiente, pueden
verse como una evaluación de la calidad educativa de una sociedad en conjunto, y no
sólo de su sistema escolar:
Si los puntajes de un país son significativamente más altos que los de otro, no
se puede inferir automáticamente que las escuelas del primero sean más
efectivas que las del segundo, puesto que el aprendizaje comienza mucho antes
que la escolaridad y ocurre en una amplia gama de lugares, dentro y fuera de la
escuela; lo que puede concluirse legítimamente es que en el primer país el
impacto acumulado de las experiencias de aprendizaje, desde la primera
infancia hasta los 15 años, y tanto en la escuela como en el hogar, ha producido
resultados más adecuados en los terrenos que evalúa PISA.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Veamos los resultados del 2003
Lugar
País
Media
Lugar
País
Media
1
Hong Kong
560
21
Alemania
490
2
Japón
557
22
Hungría
488
3
Corea
547
23
Rusia
478
4
Nueva Zelanda
537
24
España
476
5
Finlandia
536
25
Polonia
470
6
Australia
533
26
Letonia
463
7
Canadá
533
27
Italia
457
8
Suiza
529
28
Portugal
454
9
Reino Unido
529
29
Grecia
447
10
Bélgica
520
30
Luxemburgo
446
11
Francia
517
31
Israel
433
12
Austria
515
32
Tailandia
432
13
Dinamarca
514
33
Bulgaria
430
14
Islandia
514
34
Argentina
388
15
Liechtenstein
514
35
México
387
16
Suecia
510
36
Chile
384
17
Irlanda
503
37
Albania
381
OCDE
500
38
Macedonia
381
18
Noruega
499
39
Indonesia
367
19
República Checa
498
40
Brasil
334
20
Estados Unidos de
América
493
41
Perú
292
Una de las conclusiones del estudio de PISA es que no siempre un promedio más
elevado de gasto por alumno suele ir asociado a un promedio más alto de
aprovechamiento escolar, por ejemplo, aunque el gasto por alumno en Italia es dos
veces mayor que el de Corea, la República de Corea obtuvo mejores resultados en los
tres campos que Italia. Por otro lado, también se concluye que la calidad de la educación
no va siempre en detrimento de la equidad y viceversa, como lo demuestran los
ejemplos de Canadá, Finlandia, Hong Kong Japón, Corea y Suecia.
Los alumnos de Japón, Hong Kong y República de Corea se situaron a la cabeza en
matemáticas y ciencias, mientras que los alumnos de Finlandia fueron los mejores en
lectura y los alumnos de los países latinoamericanos se colocaron por debajo de la
media determinada por la OCDE (500 puntos).
Aunque es claro que las disparidades de equidades en Argentina, Brasil, Chile, México
y Perú son abismales comparadas con los países desarrollados, esto no debería
desalentar o ser un pretexto para justificar el conformismo.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Los resultados de México en PISA no deberían sorprendernos: se sitúan en el rango de
lo esperable, debido al peso de los factores socioeconómicos y a los recursos con que
pueden contar las escuelas. El desempeño promedio de nuestros alumnos no es similar
al de los países más desarrollados, pero tampoco inferior al de los que tienen un nivel de
desarrollo comparable al mexicano. Sin embargo tampoco debe quedar el pensamiento
conformista, es por eso que la capacitación docente toma un lugar protagónico para
mejorar la calidad de la enseñanza en México.
Si quiere consultar más información sobre esta prueba, puede acceder a la siguiente
dirección electrónica: http://multimedia.ilce.edu.mx/inee/pdf/PISAplus.pdf
Prueba de LLECE
La prueba LLECE es el Primer Estudio Internacional Comparativo sobre Lenguaje,
Matemáticas y Factores Asociados en Alumnos de Tercer y Cuarto Grado de
Educación Básica de 13 países de la región, reconocido como el más reciente y
relevante en su tipo para América Latina y el Caribe. Con este estudio llevado a cabo en
el año 1997 por el Laboratorio Latinoamericano de Evaluación de la Calidad de la
Educación (LLECE), se logró obtener por primera vez información comparativa acerca
de los logros de aprendizaje de los alumnos de los países de América Latina y El
Caribe, lo que refleja uno de los mayores logros políticos de los países de la región en
los años 90, porque surgió del acuerdo de 13 países de América Latina.
La información disponible para los 13 países de América Latina, que representan más
del 90% de la población en el año 2000, permite afirmar que, con excepción de Cuba, al
resto de los estudiantes latinoamericanos se les está enseñando a leer, pero no a
comprender el significado del texto ni a realizar interpretaciones. Esto confirma la
gravedad de los problemas de aprendizaje en la educación primaria de América Latina y
el por qué se obtienen estos lugares cuando se realizan evaluaciones internacionales de
rendimiento.
Aunque ningún estudio en el que hayan participado países de América Latina se ha
repetido (lo que entorpece la observación de las tendencias durante los 90), se puede
ilustrar la situación comparando los promedios de los países participantes con el de un
país desarrollado (en este caso se eligió EUA).
En la Tabla de comparación de resultados se presentan:
•
•
•
El estudio del Educational Testing Service (IAEP- International Assesement
Educational Program) en las áreas de lenguaje y matemáticas del Octavo Grado
en el año 1992;
Los estudios de la IEA en el área lenguaje en el año 1992
Los estudios del Laboratorio Latinoamericano de Evaluación de la Calidad de la
Educación (LLECE-UNESCO) en las áreas de lectura y matemáticas para el
Tercer y Cuarto Grado en 1992 y 1997;
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
•
•
El estudio “Third International Math and Science Survey (TIMSS)” en las áreas
de matemáticas y ciencias de 1995 y de 1998;
Y el estudio “Progress in Student Achievement (PISA-OECD)” en el área de
lectura, matemáticas y ciencias de la OECD realizado en el año 2000.
Como Chile, Venezuela, México, Brasil y Colombia participaron tanto en los estudios
internacionales como en los regionales es posible compararlos, tal como se hace con los
índices de precios de diversos países a través de la paridad con el dólar y formular
apreciaciones de los resultados que probablemente obtendrían si hubieran participado en
todos ellos.
Tabla. Comparación de resultados presentada en función del porcentaje de
alumnos que obtuvieron suficiencia
Países
Pruebas 1992
Pruebas 1995-2000
IEA
IAEP 92 UNESCO TIMSS
UNESCO
92 PISA 00 - Edad 15
G8
92
95&98 - G8 97 - G4
G8
Matem Ciencia Lectura
Argentina
0
Bolivia
0
Brasil
67
Colombia
0
Costa Rica
0
Chile
0
Rep.
0
Dominicana
Ecuador
0
Honduras
0
México
0
Paraguay
0
Venezuela
0
Cuba
0
Lectura
Matem Ciencia Lectura Matem Lectura Matem
0
0
79
00
00
00
0
0
0
000
00
00
66
52
0
0
70
67
0
0
00
77
0
78
0
0
0
72
0
82
83
69
82
78
0
84
79
72
79
76
0
78
0
0
77
0
0
0
0
0
68
0
0
0
00
00
56
0
0
68
69
0
0
00
00
00
00
00
00
00
00
00
00
70
0
55
0
0
0
70
0
0
0
0
0
0
0
0
0
0
0
0
0
0
70
74
74
73
103
0
68
75
73
67
104
0
0
83
0
0
0
0
0
80
0
0
0
Ciencia
0
0
75
0
0
0
0
84
0
0
0
Los niveles del aprendizaje calculados de estos países corresponden aproximadamente,
a dos tercios del nivel promedio de países desarrollados o Cuba. Estos niveles se
reducen a un 60% cuando se comparan con el mejor resultado en cada uno de los
estudios.
Esta comparación confirma el bajo nivel detectado por el Laboratorio Latinoamericano
de Evaluación de la Calidad de la Educación (LLECE) en el análisis de estos resultados.
El escaso aprendizaje se refleja en altas tasas de repetición de grados, lo que aumenta la
cantidad de alumnos en los primeros cursos y la heterogeneidad de edades, que hacen
más difícil generar situaciones de aprendizaje interesantes para todos y, eventualmente,
producen una fuerte deserción a partir de los 14 años (que es la edad en la que se ingresa
al mercado de trabajo).
Los antecedentes sobre los niveles de aprendizaje comentados en los párrafos anteriores
revelan que las estrategias impulsadas en América Latina durante las dos últimas
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
décadas no han elevado el bajo nivel de conocimientos de los alumnos de la educación
primaria. A nivel mundial se constató algo similar cuando se comprobó en Dakar la
falta de avance del programa “Educación Para Todos (EFA)”, durante la década de los
90. Esta comprobación llevó a un grupo de nueve países donantes y cuatro agencias de
financiamiento a realizar una evaluación de este proceso.
Otro de los resultados, es que los estudiantes mexicanos se colocaron por debajo de la
media en la prueba de lenguaje obteniendo un promedio de 250 puntos, siendo la media
de 261 puntos. En el caso de lenguaje, no tienen la habilidad de comprender lo que leen,
esto es sin lugar a dudas preocupante.
La conclusión general a la que llegaron en el plano de las matemáticas, a excepción de
Cuba, es que los alumnos de primaria reconocen los signos y estructuras matemáticas,
pero tienen poca capacidad para resolver problemas de la vida cotidiana.
Si quiere consultar más información sobre esta prueba, puede acceder a la siguiente
dirección electrónica: http://llece.unesco.cl/index.act
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005
Conclusiones
Como se puede ver, las conclusiones en las pruebas realizadas por PISA y por la
LLECE son similares, los alumnos tanto de secundaria como de primaria no están
preparados para resolver los problemas de la vida cotidiana, es decir, no tienen la
habilidad de aplicar el conocimiento adquirido, no están preparados académicamente
para el mundo moderno.
Este alarmante panorama ubica al profesor de cualquier nivel educativo en los
problemas metodológicos y didácticos en la enseñanza de las matemáticas, entonces:
•
•
•
¿De qué manera podemos hacer posible que la enseñanza de las
matemáticas sea más atractiva y significativa para los alumnos?
¿De que manera es posible lograr que los alumnos sean capaces de
comprender y aplicar las matemáticas en diferentes contextos?
¿De qué manera se puede contribuir a que las deficiencias
arrastradas desde la educación primaria y secundaria se vean
superadas en el nivel medio superior?
La enseñanza de las matemáticas es de una complejidad fascinante por que no sólo
basta diseñar y proponer metodologías didácticas, sino también considerar la psicología
y cognición del alumno, su contexto, su punto de partida y sus mecanismos congnitivos
de adaptación a los nuevos contenidos
Es importante reconocer que la labor del docente que imparte matemáticas no sólo debe
reducirse a solo transmitir pasivamente conocimientos o a entrenar alumnos a la
automatización de procedimientos. El profesor de matemáticas de hoy tiene la
honorable responsabilidad de ser formador y lograr que los procesos metacognitivos de
los alumnos sean eficientes de manera tal que éste comprenda, aplique y disfrute
estudiar matemáticas. Seguramente los esfuerzos individuales de cada profesor en el
aula permitirán en un futuro mejorar las estadísticas de los estudios internacionales.
De esta manera, se debe afrontar la responsabilidad que conlleva la enseñanza de las
matemáticas, cambiar la monotonía de la simple exposición de “cómo se hacen las
cosas” a una concepción más equilibrada, en donde el alumno no sólo aprenda
procedimientos, sino que aprenda el porqué, el cómo, el qué y sobre todo, el para qué.
Lograr que un grupo de alumnos llegue en las mejores condiciones al final del viaje
requiere, como se verá en los contenidos del resto de los módulos que conforman este
diplomado, del diseño, adopción e implementación de diversas estrategias que una vez
que sean probadas, den paso a un proceso de reflexión.
D.R. Vicerrectoría de Investigación y Desarrollo del Tecnológico de Monterrey, México, 2005