10/1/2014
Anuncio
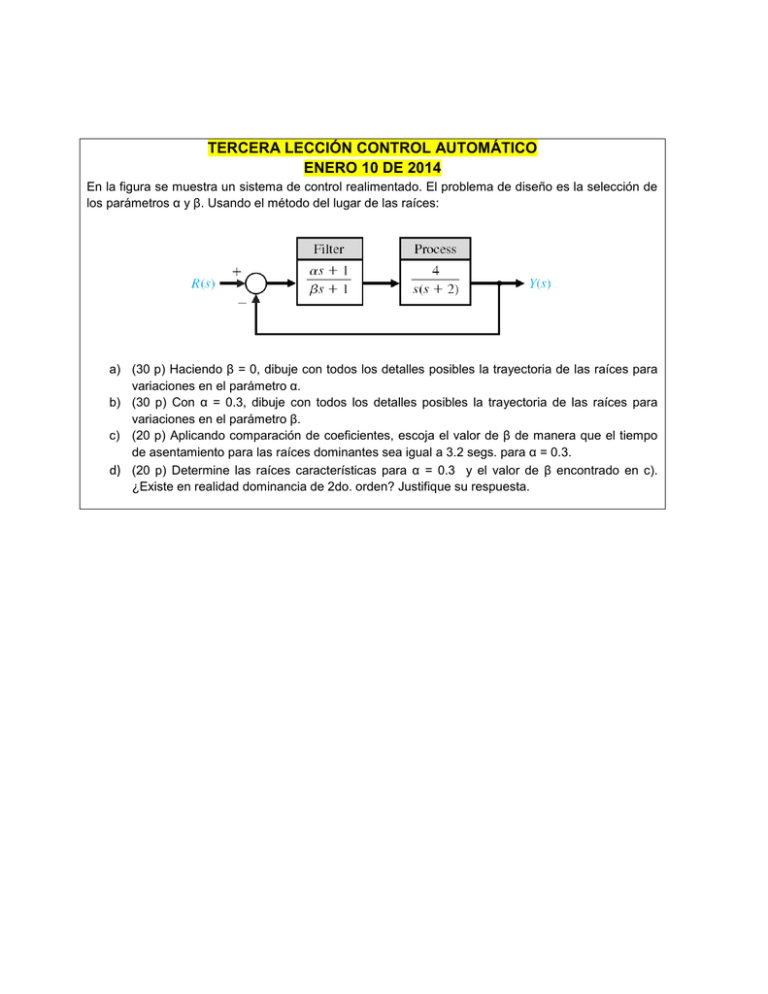
TERCERA LECCIÓN CONTROL AUTOMÁTICO ENERO 10 DE 2014 En la figura se muestra un sistema de control realimentado. El problema de diseño es la selección de los parámetros α y β. Usando el método del lugar de las raíces: a) (30 p) Haciendo β = 0, dibuje con todos los detalles posibles la trayectoria de las raíces para variaciones en el parámetro α. b) (30 p) Con α = 0.3, dibuje con todos los detalles posibles la trayectoria de las raíces para variaciones en el parámetro β. c) (20 p) Aplicando comparación de coeficientes, escoja el valor de β de manera que el tiempo de asentamiento para las raíces dominantes sea igual a 3.2 segs. para α = 0.3. d) (20 p) Determine las raíces características para α = 0.3 y el valor de β encontrado en c). ¿Existe en realidad dominancia de 2do. orden? Justifique su respuesta. Solución. a.) s 1 4 ; Gp( s ) ; H ( s) 1 s 1 s ( s 2) 4( s 1) E.C.: 1 GH ( s ) 0 1 0 s ( s 2)( s 1) Gc( s ) 0 ; 0 ; 1 K F ( s) 0 1 Asíntotas : n 2 ; m 1 Centroide : a n m 1 j 1 p j i 1 zi n m nm Angulos _ asíntotas : a 4s 4s 0 ; 1 0 s 2 2s 4 ( s 1 3 j )( s 1 3 j ) (1 3 j ) (1 3 j ) (0) 2 1 (2q 1) 180o nm ; q 0,1, 2,..., ( n m 1) a 180o Angulo _ salida _ polos _ complejos : m n i 1 k 1 k j j _ salida s j zi s j pk 180o (180 tan 1 3) 90o 180o 150o Punto _ llegada _ eje _ real : s e ; 2 2 4 d ; 4 d 2 2 e 4 e 0.5 4 e e (2 2) ( 2 2 4) 0 e 2 4 2 b.) 0.3 ; 0 ; 1 K F ( s) 0 1 Asíntotas : n 2 ; m 3 Centroide : a n j 1 p j i 1 zi n m 1 m nm Angulos _ asíntotas : a s 2 ( s 2) s 2 ( s 2) 0 ; 1 0 s 3.2s 4 ( s 1.6 1.2 j )( s 1.6 1.2 j ) 2 (1.6 1.2 j ) (1.6 1.2 j ) (2) 1.2 1 (2q 1) 180o nm ; q 0,1, 2,..., ( n m 1) 0 a 180o Angulo _ salida _ polos _ complejos : m n i 1 k 1 k j j _ salida s j zi s j pk 180o tan 1 1.2 1.2 2(180 tan 1 ) 90o 180o 87.82o 0.4 1.6 c.) 0.3 ; Ts 3.2 seg ; Ts 4 ; n 1.25 n 4( s 1) 4(0.3s 1) E.C.: 1 GH ( s ) 0 1 0 ; 1 0 s ( s 2)( s 1) s ( s 2)( s 1) s ( s 2)( s 1) 4(0.3s 1) 0 ; s 3 (2 1) s 2 3.2 s 4 0 2 1 2 3.2 4 1. s 3 s s 0 Por _ comparación _ de _ coeficientes _ con _ una _ de _ tercer _ orden : 2. ( s r )( s 2 2n s n2 ) 0 s 3 (2n r ) s 2 (2n r n2 ) s rn2 0 2 1 1 0.5 2n r 2.5 r r a. 3.2 2n r n2 2.5r n2 b. 4 4 c. rn2 ; n2 r 3.2 4 c. b. d . 2.5r 3.2r 2.5 r 2 4 r a. d 3.2 1 0.5 1 5.18 1 0.5 2 2.5 4 0.625 3.1 0.7 0 ; 0.22 2 2 d. 2 1 2 2 4 4 s s 0 s1 4.06 3 2 s 6.54s 14.54s 18.18 0 s2 1.24 1.71 j s 1.24 1.71 j 3 0.3 ; 0.22 ; s 3 Dominancia ? D D 4.06 D 5d ; 5 ; 3.28 5 d d 1.26 No _ hay _ dominancia _ de _ segundo _ grado.