Propiedades de Funciones
Anuncio

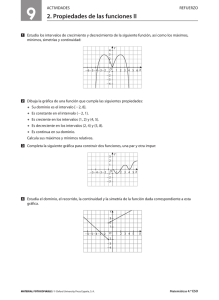
Tema: Propiedades de Funciones Descripción: Dada una función, se definirá los intervalos dónde es constante, creciente, o decreciente, positiva o negativa. Se determinará si es par o impar y si tiene máximos y/o mínimos. Ejemplo: Encontrar para la siguiente gráfica los interceptos, si los tiene, su dominio y rango, los intervalos en los cuales se mantiene constante, crece o decrece, es positiva o negativa, si es par, impar o ninguna y los intervalos en los cuales haya máximos y/o mínimos locales. a) Interceptos: (-10, 0) (-5, 0) (0, 0) (5, 0) b) Dominio: (-∞, ∞) c) Rango: (-4, ∞) d) Creciente: (-8, -2) (0, 2) (5, ∞) e) Decreciente: (-∞, -8) (-2, 0) (2, 5) f) Positiva: (-∞,-10) (-5,0) (0,5) (5, ∞) g) Negativa: (-10,-5) h) Puntos Máximos Locales: (-2, 6) (2, 10) i) Puntos Mínimos Locales: (-8, -4) (0, 0) (5, 0) j) No es par, ya que no posee simetría con respecto al eje “y”; no es impar porque no posee simetría con respecto al origen (0, 0); así que no es simétrica, o sea que es ninguna. Ejercicios: Encontrar para la siguientes gráficas los interceptos, si los tiene, su dominio y rango, los intervalos en los cuales se mantiene constante, crece o decrece, positiva o negativa, si es par, impar o ninguna y los intervalos en los cuales haya máximos y/o mínimos: 1) 2) 3) 4) Soluciones: #Ejercicio Interceptos 1 (-1,0) (0,2) (1,0) Dominio Rango Creciente Decreciente Positiva [-3,3] [0,3] (-1,0) (1,3) (-3,-1) (0,1) [-3,-1) (-1,1) (1,3] 2 (-π/2,0) (0,1) (0,π/2) [-π,π] [-1,1] (-π,0) (0,π ) (-π/2,π/2) Negativa Ø [-π,-π/2) (π/2,π] Puntos Máximos Locales o relativos: (-3,3) (0,2) (3,3) Locales o relativos: (-1,0) (1,0) Absoluto: (0,1) Es par, ya que posee simetría con respecto al eje “y”. Es par, ya que posee simetría con respecto al eje “y”. Puntos Mínimos Valor máximo de f(x) Paridad Locales o relativos: (-π,-1) (π,-1) 3 (0,0) ( 1 2 ,0) 3 4 (-2,0) (0,3) (2,0) [-2,2] [-2,2] (-1,1) (-2,1) (1,2) [2,-1) (0, 1 2 ) 3 [-1,0) ( 1 2 ,2] 3 Locales o relativos: (-2,2) (1,2) Locales o relativos: (-1,-1) (2,-2) Absoluto: (2,-2) Es ninguna, ya que no es simétrica. (-∞,∞) [0, ∞) (-2,0) (2,∞) (-∞-2) (0,2) (-∞,-2) (-2,2) (2,∞) Ø Local o relativo: (0,3) Locales o relativos: (-2,0) (2,0) Es par, ya que posee simetría con respecto al eje “y”.