Descargar este archivo PDF
Anuncio

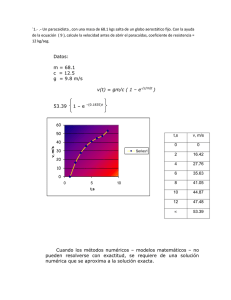
Para citar este artículo, le recomendamos el siguiente formato: Enkvist, I. (2014). La base empírica de los métodos de enseñanza de las matemáticas en la escuela primaria. Revista de evaluación educativa, 3 (1). Consultado el día de mes de año en: http://revalue.mx/revista/index.php/revalue/issue/current La base empírica de los métodos de enseñanza de las matemáticas en la escuela primaria Inger Enkvist Universidad de Lund, Suecia Bo Johansson es un investigador sueco que ha dedicado treinta años a investigar cómo aprenden los niños pequeños las matemáticas. Ha trabajado en la formación docente y ha dirigido muchas tesis de máster de didáctica de las matemáticas. Sus estudios abarcan no sólo su propia investigación empírica y la de sus estudiantes sino también la historia de la didáctica, los planes de estudio y los manuales, todo dentro del campo de las matemáticas. Vale la pena familiarizarse con sus conclusiones porque cuestionan ciertas teorías que están de moda. Sus investigaciones se han realizado en Suecia, pero es probable que los profesores e investigadores de otros países puedan sacar provecho de sus resultados. Ya que sus libros sólo están publicados en sueco y por eso inaccesibles para muchos lectores, se dará a continuación una síntesis de sus resultados, basada en los dos libros citados en la bibliografía. Se colocará entre paréntesis la traducción al inglés de los conceptos clave para que no haya confusión terminológica. En la literatura didáctica, se desprecia una enseñanza “de transmisión” y hay “verdades” no comprobadas como la idea de que sería más fácil, más “cotidiano” y más conectado con la vida del alumno el uso de objetos para calcular. El autor constata que los alumnos más “flojos” son los más perjudicados por el uso de ese enfoque. Johansson (2011) afirma que ha sido un error disminuir el recitado de la serie o la secuencia numérica (ingl. the number word sequence). Como una parte del desprecio por los conocimientos memorísticos, se ha despreciado también el conocimiento del niño de la secuencia numérica. En eso, el autor ve una similitud con la discusión sobre el aprendizaje de la lectura entre si es mejor el método global o el método fonológico. Johansson también critica que, en los manuales modernos, se presenten varios métodos como equivalentes. Supuestamente los alumnos deben elegir el método que más les guste. Esta actitud supone que todos los métodos arrojen el mismo porcentaje de respuestas correctas, lo cual no es el caso. Al revés, el investigador ha constatado repetidamente las relaciones siguientes: los alumnos a los que más tarde les va bien en aritmética son los que a la edad de 7 años saben contar por ejemplo hasta 50 o incluso hasta 100, contar al revés, “saltar” (ingl. Jump) por ejemplo de 2 a 4 a 6 y sumar algunos dobles Fecha de recepción: 30 de abril 2014 Fecha de aceptación: 18 de julio 2014 La base empírica de los métodos de enseñanza de las matemáticas en la escuela primaria. (ingl. doubles) como 2+2, 3+3 y 4+4 sin usar los dedos. Aprender a contar se puede ver como una preparación a la descontextualización que significa la aritmética. El autor compara esta preparación a la aritmética con la preparación a la lectura. Cuando el niño aprende a observar los sonidos, a encontrar rimas y a identificar si una palabra es larga o corta, aprende a distinguir entre la forma y el contenido, lo cual le prepara para entrar en el mundo de la lectura. Es fundamental que el niño aprenda a contar. Cuando el niño es muy pequeño ve el número como una cantidad de objetos, como un número cardinal. Sin embargo, puede ver el número también como ordinal, y no le cuesta nada ir de una perspectiva a otra. Muchos hablan de la necesidad de lo concreto pero el autor indica una posible nueva interpretación de la palabra concreto, y es que se podría considerar que una cifra es concreta. El alumno puede ver cada número como un elemento en una serie, lo cual le permite avanzar o retroceder en la secuencia y más tarde saltar. La secuencia numérica permite explicar cómo el niño puede pasar de ver el número como una cantidad a ver el número como un elemento de una secuencia para más tarde trabajar con el número como una cifra. Johansson propone que no se hable de abstracción en ese caso sino de dos maneras de concebir el número. Un estudio sobre la sustracción en la primaria En uno de sus estudios, Johansson ha investigado a alumnos de siete a diez años de edad, basándose en tareas de sustracción de cuatro tipos: 1. 2. 3. 4. Sin “llevar” (ingl. no regrouping required) y fáciles: 5-3; 14-2; 9-7 Sin “llevar” pero difíciles: 18-11; 37-4; 47-24 ”Llevando” en número de dos dígitos: 23-14; 26-17; 63-37 ”Llevando” en números de tres dígitos: 456-328; 345-267; 304-237 Después ha analizado los aciertos y los errores y ha entrevistado a los alumnos. Ha identificado varios métodos utilizados por los alumnos: 1. Contar (ingl. count-based method). Para calcular 8-3, los alumnos cuentan hasta 8, utilizando los dedos. Después doblan tres dedos y vuelven a contar los dedos que quedan, empezando desde el principio Es un método elemental que funciona desde una edad muy temprana. 2. La estrategia del “tipo de unidad” (ingl. place value / decompose in tens and single-digit numerals). Enfoca si la cifra representa una unidad, una decena o una centena. 3. El escribir los números en cuestión de manera vertical (ingl. vertical algorithm), por ejemplo 34-17. Este método solía usarse mucho pero desde hace unas décadas se introduce más tarde y muchos profesores dedican menos tiempo a practicarlo. 4. Saber cómo es (ingl. recall). Es el “método” de haber aprendido diferentes tablas y saber encontrar la respuesta de manera automática, “sin pensar”. 5. El “método del salto” (ingl. jump strategy). Para calcular 13-4 el alumno descompone el 4 en 3+1, quita el 3 de 13, obteniendo 10. Le falta quitar REVALUE: Revista de evaluación educativa Vol. 3, No. 1 2014 La base empírica de los métodos de enseñanza de las matemáticas en la escuela primaria. 1 y llega así a 9. El método del salto “salta” sobre el 10, buscando siempre los “compañeros de diez” (ingl. sums to ten). El alumno se encuentra así con unos números con los que está familiarizado. Se puede contar como parte del “método del salto” el apoyarse en los dobles como 3+3, 4+4 y 5+5, etcétera. Estudiando después los errores de los alumnos, el investigador se ha preguntado qué tipo errores han cometido los alumnos y si ciertos métodos llevan a menos errores que otros. Identifica tres grupos generales de errores: errores de cálculo, errores de “empezar con el número más alto” y errores de “llevar”. 1. El contar usando los dedos u otra ayuda concreta produce errores en particular con los números altos porque los niños pueden equivocarse, terminando de contar justo antes o después de la buena respuesta. El autor cree que ha sido negativo introducir dibujos de objetos en los manuales invitando a los alumnos a contar los objetos en vez de usar las cifras. 2. La estrategia de “los tipos de unidad” se puso de moda por los años 80 y 90 y produce errores si se utiliza como “atajo” cuando los alumnos todavía no dominan el “llevar”. Algunos profesores introducen problemas como 240 – 110, tratando las unidades, las decenas y las centenas como cálculos separados. En el ejemplo citado de 240 – 110 sería tratar el problema como tres cálculos separados: 2-1, 4-1 y 0-0. Hasta hay profesores que enseñan a los alumnos que pueden empezar desde la izquierda y continuar hacia la derecha. En los casos sencillos como el expuesto, se llega a la respuesta esperada pero por ejemplo con 240 195 no. Los alumnos habrán aprendido un método que les da resultados equivocados en muchos casos. En conexión con este método surge a veces el error de “primero el más grande”. Cuando se calcula 26-17, el alumno que no sabe qué hacer con 6-7 “prefiere pensar” que podría calcular 7-6, es decir, da vuelta a las cifras porque no maneja bien el “llevar”. 3. El sistema de colocar los números de manera vertical, el uno bajo el otro, para realizar el cálculo da buen resultado en particular para los números de tres dígitos, pero hace falta que los alumnos practiquen el método para que les salga bien. 4. Funciona bien el “método” de “saber” la respuesta, es decir, de haber aprendido las tablas de adición, sustracción y multiplicación. 5. El método del salto es eficaz. En otras palabras, ¿qué métodos enseñar según esta investigación? Son negativos los métodos que se apoyen en contar objetos, y en particular para los alumnos más flojos. Es eficaz aprender a ver mentalmente la secuencia de números para poder “saltar”. Los métodos más eficaces son el salto y la colocación vertical, además del método de “saber”. El método del salto se enseña de manera muy consciente en países como Holanda, Japón y Corea que tienen buenos resultados. Varias investigaciones subrayan que para poder REVALUE: Revista de evaluación educativa Vol. 3, No. 1 2014 La base empírica de los métodos de enseñanza de las matemáticas en la escuela primaria. resolver problemas complejos más tarde, la aritmética tiene que funcionar con casi un 100 % de respuestas correctas. La secuencia numérica mental como instrumento didáctico Johansson (2013) nos recuerda que los adelantos de la Medicina se basan en comparar la eficacia de diferentes métodos y, por eso, lamenta la poca base empírica de las propuestas de diferentes métodos de enseñanza. El resultado fundamental al que ha llegado él es que el uso de la secuencia mental de números es fundamental para poder usar las matemáticas y que ningún método que no se base en ella funciona bien. El énfasis en lo concreto ha sido un callejón sin salida en particular para los alumnos con problema. Johansson insiste en que la secuencia numérica permite explicar cómo llega un niño a crear conceptos. Primero ve un número como cierta cantidad pero después aprende a ver una cifra como un elemento que pertenece a una secuencia ordenada, lo cual es el verdadero comienzo del aprendizaje. Cuando el niño domina la secuencia numérica se le abre la posibilidad de usar el método del salto. El método del salto se caracteriza por: - Dejar uno de los números intacto. - El otro número se descompone para “saltar” sobre el 10. - Los números se ven como cifras. - La atención está en las cifras y en la relación entre ellas. Si el alumno entiende esto, tiene una base para trabajar con los números como conceptos. Johansson ha oído decir una y otra vez a las maestras del nivel preescolar que las cifras son difíciles. No, dice él, no son difíciles. Esta creencia falsa hace que se retrase el aprendizaje. También ha oído que el saber enumerar la secuencia numérica no significa necesariamente que el alumno entienda lo que está diciendo y que, por eso, es inútil practicar esa destreza. Error, dice Johansson. Cuanto mejor sepa contar la secuencia numérica y cuanto antes sepa escribir las cifras, mejor le irá al alumno en matemáticas. Es falso que las cifras sean difíciles, es falso que sea inútil practicar la secuencia numérica y es falso que sea más natural y provechoso para los alumnos ver los números como cantidades y no posiciones en una serie. Al revés, constata, saber las tablas de adición, sustracción y multiplicación es fundamental para el avance del alumno porque el alumno calcula de manera más rápida, comete menos errores y sabe realizar cálculos más complejos. Johansson da cuenta de varios proyectos que muestran que si el profesor trabaja conscientemente para enseñar la secuencia numérica y los saltos, los alumnos progresan rápidamente y los más flojos son los que más avanzan. El método del salto fue el método más utilizado en el siglo XIX pero alrededor de 1900 se lanzó la idea de que sería más fácil para el niño aprender en conexión con lo concreto y lo cotidiano. Por los años 60 y 70 se añadió la tendencia a dar énfasis al “tipo de unidad”. Sin embargo, los nuevos métodos REVALUE: Revista de evaluación educativa Vol. 3, No. 1 2014 La base empírica de los métodos de enseñanza de las matemáticas en la escuela primaria. introducidos han supuesto un retraso en particular para los niños con problema. El investigador se asombra de la insistencia en lo cotidiano y lo concreto porque eso corresponde a lo que el niño ya sabe y no a lo que el niño necesita aprender. En términos de Vygotsky, se debería buscar la zona del próximo desarrollo y no la del aprendizaje ya realizado. Además, no solo se busca la habilidad de resolver problemas sino también la comprensión de los conceptos. El investigador resalta que sus resultados son unívocos y estables: conocer las cifras y la secuencia numérica es la base del aprendizaje. No importa la edad del niño ni su “maduración” sino si ha aprendido o no. Además, los niños que manejan la secuencia numérica se acuerdan mejor de diferentes números, lo cual a su vez mejora su capacidad matemática. Johansson rechaza que el placer deba ser el motor del aprendizaje. Al revés, el placer aparece cuando el niño domina el método en cuestión. Reflexiones ¿Cómo se ha llegado a la situación actual? Johansson cree que una razón es que se ha considerado que la didáctica debía modernizarse y democratizarse, introduciendo nuevos métodos que supuestamente iban a permitir un aprendizaje más fácil y más igualitario. Los pedagogos que introdujeron los métodos no tenían un entrenamiento sólido ni en las matemáticas ni en la estadística y prefirieron evaluar sus proyectos según si los profesores y alumnos estaban contentos y no según si había mejorado el resultado. Más bien, se decía que el resultado buscado era que los alumnos tuvieran una actitud positiva hacia la escuela. Además se buscaba que todos tuvieran un resultado similar y no que avanzaran todos lo más posible. Johansson subraya que si la escuela quiere obtener resultados debe proceder como las ciencias exitosas. Curiosamente había en Suecia alrededor de 1840 algo llamado una escuela para niños pequeños (ingl. infant school). En esa escuela había una enseñanza basada en la secuencia numérica. Llegaron a aprender mucho los niños, pero eso mismo disgustó a algunos pedagogos que consideraban que se forzaba demasiado el aprendizaje y que los niños debían aprender “a su propio ritmo”. Fue tan criticada la escuela para niños pequeños que desapareció. Desde entonces, la mantra mil veces repetida es que la enseñanza debe ser concreta y cotidiana y basarse en las observaciones y preguntas formuladas por los propios niños. Esta manera de ver ha sido tan dominante que ni siquiera se denomina con un término especial. Cuando alrededor de 1970 se empieza a hablar del constructivismo se trata de una continuación de este pensamiento. Una manera “gramatical” de describir las diferencias entre el método constructivista y el que propone Johansson sería hablar de los números como adjetivos o como sustantivos. Cuando se quiere ser concreto y contar usando los dedos, unos bloques de madera o unas ovejas dibujadas, el número se usa como adjetivo. Lo principal de la atención se enfoca en los dedos, los bloques o las ovejas. El contar usando los números como cifras en una secuencia es usar los números como sustantivos. Las cifras se bastan a sí mismas y constituyen el centro de la atención. REVALUE: Revista de evaluación educativa Vol. 3, No. 1 2014 La base empírica de los métodos de enseñanza de las matemáticas en la escuela primaria. Johansson subraya que la secuencia numérica y la consiguiente posibilidad de saltar explican el camino del alumno hacia los conceptos matemáticos. El constructivismo no sabe explicar cómo pasa el alumno de los bloques de madera al cálculo con números elevados. La explicación de Johansson es la siguiente. Cuando un alumno entiende los números de la secuencia sin referencia a una situación concreta está formando conceptos. Cuando entiende que 4+5 son 9 porque con 4+4 tiene 8 y debe añadir 1 más y así obtiene 9, ha entendido cómo son los números y ha entendido que podría realizar el cálculo empezando con 5+5, que son 10, y después quitar 1. De ahí, es sólo un paso para entender que 40 + 50 se calcula del mismo modo. Johansson dice que lo que hace el alumno es usar la reflexión y que para reflexionar hace falta precisamente haber elaborado conceptos. Pensar es usar conceptos; es partir de un concepto para ir a otro. Pensar es manipular conceptos mentalmente. En la aritmética, esto significa dejar atrás los dedos, los bloques de madera y los dibujos de ovejas y centrarse en las cifras. Así, el alumno está preparado para el pensamiento hipotético en otras áreas y así la enseñanza de matemáticas sirve de instrumento intelectual más allá de los límites de la propia matemática. Para concluir, Johansson cree que el constructivismo ha sido negativo para el aprendizaje de las matemáticas. Sus resultados dicen claramente que el aprender a contar y a usar la secuencia numérica es lo decisivo para el éxito y no lo concreto ni lo cotidiano ni la iniciativa del propio alumno. Bibliografía Johansson, Bo. Matematik i förskola och förskoleklass. Den mentala talraden som didaktiskt verktyg. Stockholm, Kunskapsföretaget, 2013. ___. Varför är subtraktion svårt? Orsaker och förslag till åtgärder. Stockholm, Kunskapsföretaget, 2011 REVALUE: Revista de evaluación educativa Vol. 3, No. 1 2014