cónicas

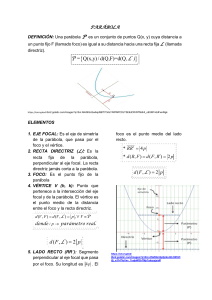
CÓNICAS
CIRCUNFERENCIA
Definición : Lugar geométrico de los puntos del plano (P) que equidistan ( R ) de otro punto
llamado Centro (C)
Ecuaciones:
( x − a ) 2 + ( y − b) 2 = R 2
1.- Aplicando dist. (P(x,y), C(a,b)) = R; obtenemos
2.- Desarrollando:
a=
2
2
x + y + mx + ny + p = 0 donde, m = -2a n = -2b
−
m
2
b=
−
n
2
p = a2 + b2 _ R2, es decir:
R2 = a2 + b2 - p
Ecuación de una circunferencia centrada en el O(0,0):
x2 + y2 = 0
Circunferencias concéntricas: x2 + y2+ mx + ny + p1 = 0 ; x2 + y2+ mx + ny + p2 = 0
RECTAS TANGENTES a una circunferencia :
1.-En un punto de ella: el vector que une el centro y dicho punto es perpendicular a la tangente
2.-En un punto exterior: doble solución, poner la recta tangente en la forma pto-pte y la distancia
del centro de la circunferencia a la recta tangente es el radio (ver ejemplos clase)
ELIPSE
Definición: Lugar geométrico de los puntos del plano cuyas suma de distancias a dos punto fijos
I
llamados focos ( F y F ) ,es constante. (Sustituyendo P=A, se observa que la constante es 2.a )
•
•
Eje focal: La recta que pasa por los focos.
•
Eje secundario: mediatriz del segmento que une F y FI
•
Distancia focal, es la distancia entre los focos, 2c.
F(c,0) y FI(-c,0)
•
Vértices : Los puntos en los que la elipse corta al eje focal y al secundario.A(a,0), AI(-a,0B(b,0)
y BI(-b,0)
B
a
I
•
Eje Mayor: Segmento que une A y A , 2a . Semieje mayor : a
I
•
Eje Menor: Segmento que une B y B , 2b . Semieje menos. b
b
F
F
•
Centro de la elipse O, es el punto de intersección de los ejes. AI
A
c
I
Ecuación: De |PF| +| PF | = 2a , la ecuación de ELIPSE CENTRADA EN EL ORIGEN , eje mayor 0X y
menor OY.
x2 y2
+
=1
a2 b2
donde: a2= b2 + c2
( sustituyendo P=B; |BF|+|BFI|=2.a ; |BF|=b2+c2)
EXCENTRICIDAD: e=c/a (siempre será e<1)
Cuanto más próxima a 1 sea e la elipse será más achatada, si e=0 será una circunferencia
( ya que si e=0, c=0 y a=b)
HIPÉRBOLA
Definición: Lugar geométrico de los puntos del plano cuyas diferencia de distancias a dos punto
I
fijos llamados focos ( F y F ) ,es constante. (Sustituyendo P=A, se deduce que la constante es 2a
•
Eje focal: La recta que pasa por los focos. (eje real)
•
Eje secundario: mediatriz del segmento que une F y FI (eje imaginario)
•
Distancia focal, es la distancia entre los focos, 2c.
F(c,0) y FI(-c,0)
•
Vértices : Los puntos en los que la hipérbola corta al eje focal A y AI
•
Centro de la hipérbola O, es el punto de intersección de los ejes.
•
Eje real o mayor, 2.a
•
Eje imaginario, 2b
Ecuación: De |PF| -| PFI| = 2a , la ecuación de HIPÉRBOLA CENTRADA EN EL ORIGEN ,
eje mayor 0X y menor OY.
x2 y2
−
=1
a2 b2
2
2
ASÍNTOTAS DE LA HIPÉRBOLA
Recta que pasa por su centro y es tangente a
ella en el infinito
Ecuaciones de las asíntotas de una hipérbola
centrada en el origen:
2
donde b = c – a
Excentricidad Hipérbola: e=c/a
Siempre será e>1, pues el
semieje menor es siempre
mayor que la semidistancia focal
y=
b
x
a
e
y=-
HIPÉRBOLA EQUILÁTERA
Es una hipérbola cuyo semieje real es igual al semieje imaginario, a = b.
Ecuación : x2 - y2 = a2 Asíntotas: y =x y =-x
Excentricidad: e =
b
x
a
Hipérbola
equilátera
y=1/x o
y.x=1
2
Si cambiamos los ejes a las bisectrices la ecuación será:
y=
k
x
con k =
a2
2
. Asíntotas, eje x y eje y
Nota : La representación gráfica de la
función de proporcionalidad inversa es
una hipérbola.
PARÁBOLA
Definición: Es el lugar geométrico de los puntos del plano que equidistan de una recta llamada directriz,
y de un punto llamado foco.
p
•
Parámetros de la parábola, p, es la distancia entre entre el foco y la directriz.
•
Eje de la parábola, es la perpendicular a la directriz que pasa por el foco.
• Vértice, es el punto de intersección de la parábola con su foco
O
Ecuaciones:
y2 = 2px
PARÁBOLA CON CENTRO (0,0) Y EJE HORIZONTAL, F(P/2,0)
X2 = 2py
Nota:
Las parábola de eje vertical , que no
pase por el O(0,0) tienen la expresión
y = ax2 + bx + c ,
son con las que hemos trabajado.
Recordar el vértice era
xV= - b
2a
directriz
PARÁBOLA CON CENTRO (0,0) Y EJE VERTICAL, F(P/2,0)
; la y sustituíamos para calcular
su valor.
Si a>0 era convexa, si a<0 cóncava
I.E.S Profesor Máximo Trueba
Nota:
Las parábola de eje horizontal que no pase
por el O(0,0) tiene la ecuación la expresión x
= ay2 + by + c
El vértice era yV = - b
2a
; la x sustituíamos para
calcular su valor.
Si a>0 las ramas van hacía la derecha
Si a<0 hacía la izquierda
a>0
a<0
V
Profesora: Rosa Hernández Gila
o
F(p/2,0)