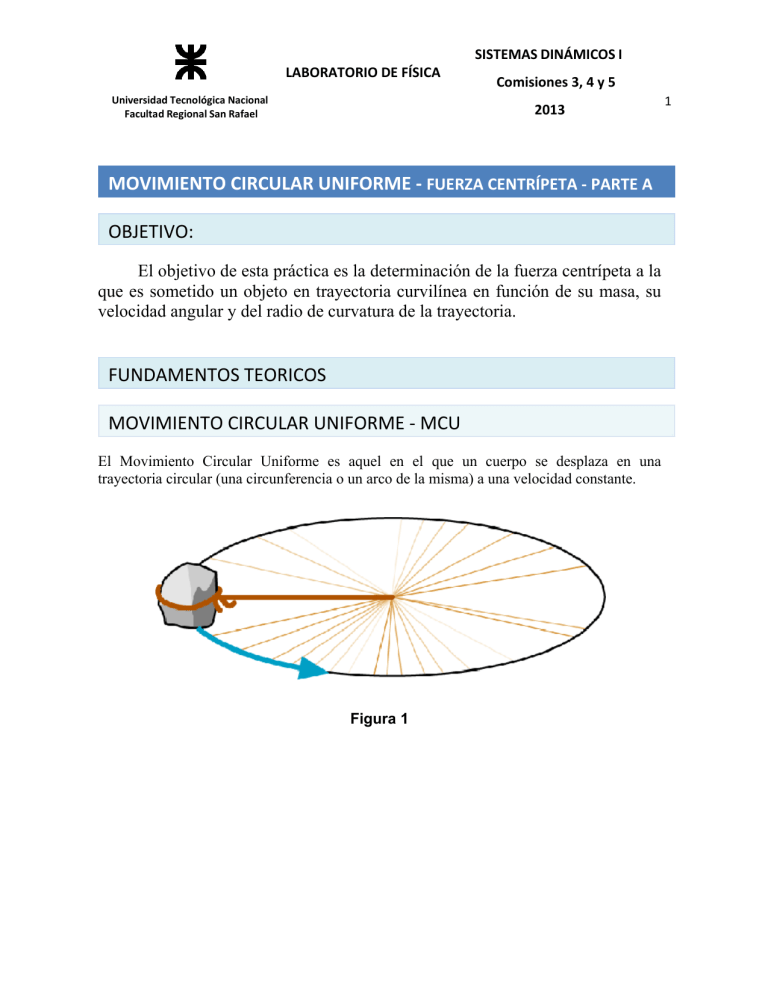
SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 2013 MOVIMIENTO CIRCULAR UNIFORME ‐ FUERZA CENTRÍPETA ‐ PARTE A OBJETIVO: El objetivo de esta práctica es la determinación de la fuerza centrípeta a la que es sometido un objeto en trayectoria curvilínea en función de su masa, su velocidad angular y del radio de curvatura de la trayectoria. FUNDAMENTOS TEORICOS MOVIMIENTO CIRCULAR UNIFORME ‐ MCU El Movimiento Circular Uniforme es aquel en el que un cuerpo se desplaza en una trayectoria circular (una circunferencia o un arco de la misma) a una velocidad constante. Figura 1 1 SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Comisiones 3, 4 y 5 Universidad Tecnológica Nacional Facultad Regional San Rafael 2 2013 y v F x Figura 2 Ángulo y velocidad angular El ángulo abarcado en un movimiento circular es igual al cociente entre la longitud del arco de circunferencia recorrida y el radio. La longitud del arco y el radio de la circunferencia son magnitudes de longitud, por lo que el desplazamiento angular es una magnitud adimensional, llamada radián. Un radián es un arco de circunferencia de longitud igual al radio de la circunferencia, y la circunferencia completa tiene 2 , radianes. La velocidad angular es la variación del desplazamiento angular por unidad de tiempo: (1) Partiendo de estos conceptos se estudian las condiciones del movimiento circular uniforme, en cuanto a su trayectoria y espacio recorrido, velocidad y aceleración, según el modelo físico cinemático. Posición Se considera un sistema de referencia en el plano xy, con vectores unitarios en la dirección de estos ejes (O; i,j) . La posición del cuerpo en función del ángulo de giro y del radio r es en un sistema de referencia cartesiano xy: SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 3 2013 (2) De modo que el vector de posición de la partícula en función del tiempo es: (3) siendo: r: es el vector de posición de la partícula. r: es el radio de la trayectoria. Al ser un movimiento uniforme, a iguales incrementos de tiempo le corresponden iguales desplazamientos angulares, lo que se define como velocidad angular (ω): (4) ⟹ El ángulo ( ), debe medirse en radianes: (5) donde s es la longitud del arco de circunferencia Según esta definición: 1 vuelta 360° 2 π radianes ½ vuelta 180° π radianes ¼ de vuelta 90° π /2 radianes Velocidad tangencial La velocidad se obtiene a partir del vector de posición mediante derivación tangencial: SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 4 2013 (6) en donde se ve la relación entre la velocidad angular y la velocidad tangencial (7) El vector velocidad es tangente a la trayectoria, lo que puede comprobarse fácilmente efectuando el producto escalar . y comprobando que es nulo. Aceleración La aceleración se obtiene a partir del vector velocidad con la derivación: (8) De modo que (9) Así pues, el vector aceleración tiene dirección opuesta al vector de posición, normal a la trayectoria y apuntando siempre hacia el centro de la trayectoria circular. por lo que acostumbramos a referirnos a ella como aceleración normal o centrípeta. El módulo de la aceleración es el cuadrado de la velocidad angular por el radio de giro, aunque lo podemos expresar también en función de la celeridad , de la partícula, ya que, en virtud de la relación resulta (10) Esta aceleración es la única que experimenta la partícula cuando se mueve con rapidez constante en una trayectoria circular, por lo que la partícula deberá ser atraída hacia el centro mediante una fuerza centrípeta que la aparte de una trayectoria rectilínea, como correspondería por la ley de inercia. SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 5 2013 Período y frecuencia El periodo dado por: , representa el tiempo necesario para que el móvil complete una vuelta y viene 2 (11) La frecuencia mide el número de revoluciones o vueltas completadas por el móvil en la unidad de tiempo y viene dada por: 2 (12) Por consiguiente, la frecuencia es el recíproco del período: 1 (13) Fuerza centrípeta Cuando un cuerpo de masa se mueve con un movimiento circular uniforme experimenta una fuerza centrípeta F como es representada en la ¡Error! No se encuentra el origen de la referencia.. SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 6 2013 Figura 3 El módulo de la fuerza centrípeta | | corresponde a: (14) | | Donde es la velocidad tangencial, la velocidad angular y es el radio de la trayectoria circular que describe el cuerpo. Dado que: 2 corresponde al periodo de oscilación de la masa (15) . Remplazando la Ec. (2) en la Ec. (1) tenemos: | | 4 (16) PÉNDULO CÓNICO El péndulo cónico está constituido por un cuerpo pesado de pequeñas dimensiones (puntual, idealmente) suspendido de un punto fijo mediante un hilo inextensible y de masa despreciable. Su construcción es la misma que la de un péndulo simple, pero, a diferencia de éste, el péndulo cónico no oscila, sino que la masa pendular describe una trayectoria circular en un plano horizontal con aceleración constante. Su nombre proviene del hecho de que el hilo traza una superficie cónica. El péndulo cónico es un caso particular del péndulo esférico. En concreto es un péndulo esférico en el que el vector velocidad (inicial) es perpendicular al plano determinado por la vertical y el hilo. SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 7 2013 Figura 4 Consideremos un péndulo cónico consistente en una pequeña esfera de masa m que se mueve sin fricción en una circunferencia horizontal con una celeridad constante v, suspendida de un hilo de longitud L que forma un ángulo constante θ con la vertical. Sobre la masa m actúan dos fuerzas: su propio peso, mg, y la tensión del hilo, T. La componente horizontal de la tensión del hilo proporciona la aceleración centrípeta, , asociada con el movimiento circular. La componente vertical de la tensión se compensa exactamente con el peso de la masa m. La aplicación de la segunda ley de Newton en las direcciones horizontal y vertical nos permite escribir: (17) (18) Dividiendo miembro a miembros estas dos ecuaciones, eliminamos T y m, resultando: SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 8 2013 ⇒ (19) Puesto que la celeridad v es constante, puede expresarse en función del tiempo Tp, requerido para realizar una revolución completa o periodo de revolución 2 (20) y sustituyendo en la ecuación (19) la anterior, después de fáciles operaciones, obtenemos: 2 (21) En la ejecución práctica de la experiencia, r varía y no es tan fácil de medir como la longitud constante L del hilo. Recurriendo a la relación trigonométrica entre r, h, y L, esto es, , la relación (21) se escribe en la forma: 2 (22) PROCEDIMIENTO DE LABORATORIO Equipo necesario Cantidad 1 1 1 Equipamiento y materiales PASPORT Xplorer GLX PASPORT Sensor de Fuerza Kit Discover de Fuerza centrípeta Part Number PS-2002 PS-2104 ME-9837 1 1 1 1 Abrazadera de mesa universal Rod, 45 cm Reglametrica Lapicera ME-9376B ME-8736 SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 2013 Actividad A Seleccione una de las masas de goma, sujetar Usar el sensor de fuerza para medir la fuerza centrípeta aplicada a una masa que se mueve en un círculo a diferentes velocidades. Utilice el Xplorer GLX para registrar y mostrar la fuerza. Determinar el período de movimiento de la masa que gira y calcular su velocidad circular. Comparar la fuerza centrípeta a la velocidad circular. Figura 5 1. Puesta en funcionamiento del equipo [1] Encienda el GLX y abra el archivo de instalación GLX etiquetado como velocidad centrípeta. • El archivo se abre con una pantalla gráfica que muestra la fuerza, tiro positivo (N) frente al tiempo (s). El archivo está configurado para medir la fuerza de 100 veces por segundo (100 Hz). (Nota: Si la pantalla gráfica muestra la "velocidad circular (m /s)" y "fuerza promedio (n)" en lugar de la fuerza, tiro positivo, pulse F4 ( ) para abrir el menú Gráficos y seleccione "Gráfico 1 “. Presione para activar su elección. En este paso se verá la pantalla indicada en la Figura 9 Fig. 1: GLX Graph SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 2013 10 Figura 6 Pantalla grafica del GLX [2] Conecte el sensor de fuerza en un puerto sobre la parte superior de la GLX. 2. Configuración del equipo [1] Utilice un precinto y la varilla para montar el sensor de fuerza con su extremo de gancho como se muestra en la Figura 7. Figura 7 Setup del sensor. [2] Fije un precinto de plástico a través del centro del disco de goma. [3] Ate un trozo de 1,5 m de cuerda al precinto plástico. Pase la cuerda a través del tubo hueco del kit. Ate el otro extremo al gancho en el sensor. [4] Use un marcador y una regla para hacer marcas en la cuerda a los 10, 20, 30, 40, y 50 cm desde el centro del tapón. [5] Finalizado el montaje del equipo se verá como en la Figura 8. SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 2013 Figura 8 Equipo listo para su uso. 3. Grabar datos NOTA: El procedimiento es más fácil si una persona maneja el equipo, una segunda persona verifica el radio, y un tercero se encarga de la Xplorer GLX. 4. Velocidad Angular: radio y masa constantes. [1] Presione el botón ZERO en el sensor. [2] Haga girar el tapón en un círculo horizontal de radio fijo (prueba de 50 cm o 0,5 m) por encima de su cabeza (Figura 9). Registre la el radio que está utilizando en la tabla de datos. Figura 9 Modo de giro del disco. 11 SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 2013 [3] Cuando usted es capaz de girar el disco a una velocidad constante, pulse Iniciar ( ) para comenzar con el registro de datos. [4] Después de más de 7 revoluciones, presione para detener la grabación de datos. Nota Si al observar el gráfico de la fuerza en función del tiempo se muestran 7 o más ciclos de oscilación consistentes (con forma sinusoidal), continúe a la siguiente parte; Si no es así, repita los pasos anteriores. 5. Análisis de los Datos. Obtenga el período haciendo uso del gráfico de tiempo vs. fuerza. Utilice el periodo y el radio para calcular la velocidad tangencial. Use la gráfica para encontrar la fuerza media. [1] Coloque escala automática en el grafico de la pantalla, si es necesario (pulse F1). [2] Utilice las teclas de flecha para mover el cursor a uno de los picos en el grafico. [3] Utilice la “herramienta de Delta (Delta Tool)” para encontrar el tiempo de por lo menos 7 revoluciones. Pulse F3 ( ) para abrir el menú “Herramientas”, “Delta Herramienta”. Seleccionar y pulsar ) para activar su elección (Figura 10). Figura 10 Seleccionar ‘Delta Tool’. [4] Utilice las teclas de flecha para mover el cursor a un pico y cuente por lo menos 7 revoluciones desde allí, seleccione el próximo pico. Registre el tiempo de las revoluciones en la tabla de datos. [5] Cuente el número de revoluciones y registre el número en la tabla de datos. [6] Divida el tiempo por el número de revoluciones para calcular el período (de una oscilación) (Figura 11). Registre el valor. 12 SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Universidad Tecnológica Nacional Facultad Regional San Rafael Comisiones 3, 4 y 5 2013 13 Figura 11 [7] Calcule la velocidad circular en base al radio y el período. [8] Use la herramienta “Estadísticas” para encontrar la fuerza media. Pulse para abrir el menú “Herramientas” y seleccione “Estadísticas”. Pulse para activar su elección. [9] Anote valor “Avg” como la “fuerza media” en la tabla de datos. 6. Para las otras velocidades: Con radio fijo y masa constante. [1] Repita el registro de datos y "sobre el problema en análisis” utilizando el mismo radio y el mismo tapón, tome siete velocidades más. [2] Registre sus resultados en la tabla de datos para cada ejecución. [3] • Para cambiar la pantalla de gráficos y mostrar una ejecución específica de los datos, presione para activar el rótulo. Pulse las teclas de flecha ( ) para desplazarse a “Ejecutar # “ en la esquina superior de la pantalla. [4] Pulse para abrir el menú, seleccione los datos que se ejecutan en el menú y pulse para activar su elección. 7. Crear un gráfico: Velocidad Circular vs. fuerza media. Crear un gráfico de la velocidad tangencial frente a la fuerza media con la velocidad en el eje vertical. [1] Para crear un gráfico de la velocidad tangencial frente a la fuerza media, comience con una tabla en la que pueda introducir sus datos. Pulse para entrar en la pantalla de inicio. Presione F2 en el icono de la tabla ( ) para abrir la pantalla de la tabla. • La pantalla de la tabla tiene dos columnas tituladas "velocidad circular (m / s)" y "fuerza media (n)". SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Comisiones 3, 4 y 5 Universidad Tecnológica Nacional Facultad Regional San Rafael 14 2013 [2] Utilice las teclas de flecha para seleccionar la primera celda en "velocidad circular (m / s)". Pulse F2 (Editar Celda) para seleccionar la celda activa para la edición. Utilice las teclas alfanuméricas para introducir el valor de la velocidad circular para la primera carrera (de la tabla de datos). Pulse para activar la entrada. • La siguiente celda de la columna se selecciona automáticamente. [3] Introduzca el siguiente valor de la velocidad circular y presione para activar su entrada (y automáticamente selecciona la tercera celda). Continúe introduciendo el resto de los valores para velocidad Circular y presionar cada vez para activar la entrada y seleccionar la siguiente celda. [4] Presiona Esc ( ) y utilice las teclas de flecha para seleccionar la primera celda en "media fuerza (n)". Pulse F2 para que activar la celda para su edición. Utilice las teclas alfanuméricas para introducir el valor de la fuerza media para la primera carrera (de la tabla de datos). Pulse para activar la entrada (y automáticamente selecciona la siguiente celda de la columna). [5] Entre el resto de los valores de fuerza media y presione para activar cada entrada (y automáticamente selecciona la siguiente celda). [6] Cuando haya terminado, pulse para volver a la pantalla principal. [7] Pulse F1 para abrir la pantalla de gráficos. En el gráfico, presione F4 para abrir el menú "Gráficos". Seleccione “Gráfico 2” (en la parte inferior del menú) y presione para activar su elección. [8] • “Gráfico 2” tiene ”velocidad circular (m/s)”sobre el eje vertical y “fuerza media (n)” en el eje horizontal. [9] Dibuje la gráfica de la velocidad circular frente a la fuerza media en el Informe de Laboratorio. Registre sus resultados y responda las preguntas de la sección. ACTIVIDADES Una masa se mueve en un círculo y el radio del círculo se mantiene constante. ¿Cómo cambiaría la fuerza centrípeta si la velocidad de la masa se incrementara? Tabla de Datos. Velocidad tangencial: radio y masa constantes. Radio (m) idem Tiempo (s) Revoluciones Periodo (s) Velocidad tang (m/s) Fuerza media (N) SISTEMAS DINÁMICOS I LABORATORIO DE FÍSICA Comisiones 3, 4 y 5 Universidad Tecnológica Nacional Facultad Regional San Rafael 2013 15 idem idem idem idem idem Cálculos Calcule el periodo dividiendo el tiempo por el número de revoluciones. Calcule la velocidad tangencial en base al radio y al período Dibuja la gráfica de la velocidad tangencial frente a la fuerza media para los datos. Incluya las etiquetas y las unidades en los ejes. Preguntas 1. ¿Cómo varia la fuerza centrípeta cuando la velocidad tangencial de un objeto aumenta? 2. ¿Cuál es la forma de la gráfica de la velocidad tangencial frente a la fuerza promedio? (Ejemplo: lineal, parabólica, inversa, del cuadrado inverso, etc.) 3. Use palabras (o una expresión matemática), que describan la relación aparente entre la fuerza centrípeta y velocidad tangencial para el movimiento circular uniforme cuando la masa y el radio son constantes. 4. ¿Sus resultados apoyan su predicción? INFORME Elaborar un informe con las experiencias de laboratorio y las actividades solicitadas. Entregar el mismo al docente a cargo.