Guía de Actividades GeoGebra: Funciones Afines y Lineales
Anuncio
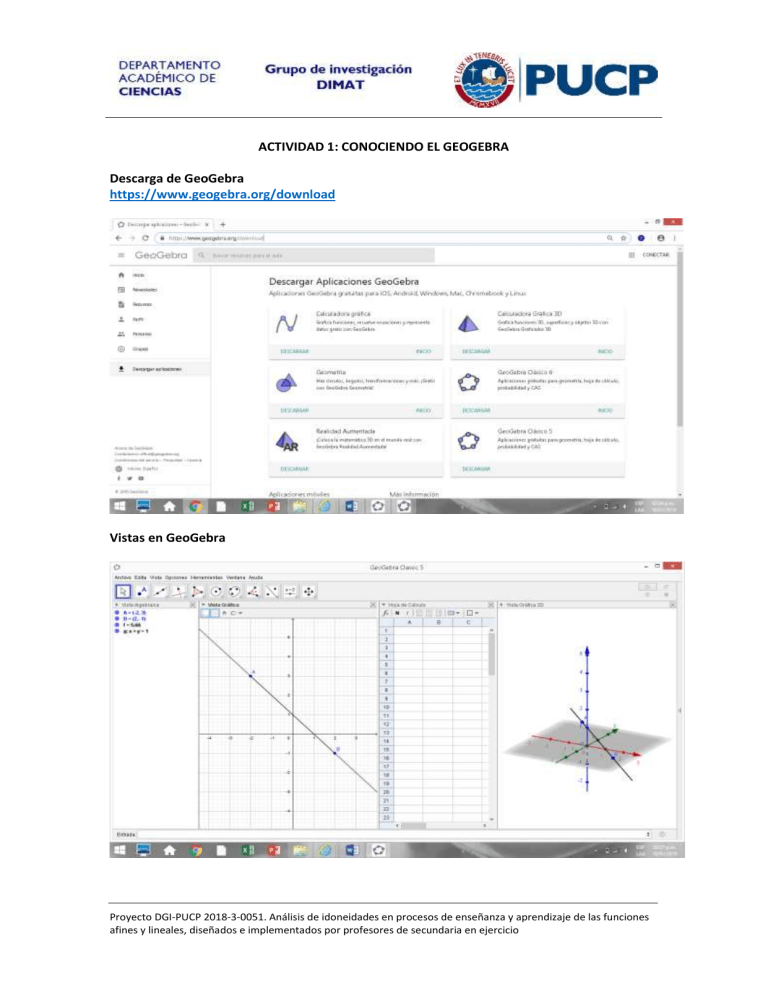
ACTIVIDAD 1: CONOCIENDO EL GEOGEBRA Descarga de GeoGebra https://www.geogebra.org/download Vistas en GeoGebra Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio Barra de herramientas de GeoGebra Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio Construcción de un punto, un segmento y una recta 1. Abra Nueva ventana en GeoGebra. 2. Active la opción Punto y haga click en la cuadricula en el punto de coordenadas (3, 2). 3. Haga click derecho sobre el punto trazado en la cuadricula y con la opción Renombra denótelo con la letra P. 4. En la barra de entrada escriba 𝑄 = (8, −5) y pulse ENTER. 5. Active la opción Segmento 6. Active la opción Recta ⃡ . 𝑃𝑄 y una los puntos P y Q. y una los puntos P y Q. En la Vista gráfica aparece la recta Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio 7. En la barra de entrada, escriba la ecuación 𝑦 = 2𝑥 + 1. Observamos que en la Vista gráfica aparece la recta correspondiente a dicha ecuación. 8. Active la opción Intersección y haga click sobre cada una de las rectas trazadas. Ubique el cursor sobre el punto de intersección que aparece en la Vista gráfica, en este caso aparece denotado con la letra B, y haga click derecho. En el cuadro Punto B que aparece, elija la opción Propiedades. Luego, aparece otro cuadro con el título Propiedades de Punto B, allí elija en Etiqueta visible, Nombre y valor. Construcción de un punto sobre un objeto y animación de un punto 1. Abra Nueva ventana en GeoGebra. 2. Active la opción Recta y haga click en dos puntos cualesquiera del plano. Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio 3. Active la opción Punto en objeto y haga click sobre la recta trazada anteriormente. Denote dicho punto con la letra Q. 4. Deslice el punto Q sobre la recta. 5. Ubique el cursor sobre el punto Q y haga click derecho. En el cuadro Punto Q que aparece, elija la opción Animación. Observe como inmediatamente el punto empieza a deslizarse a lo largo de la recta. Para detener la animación de click en el botón que aparece en la parte inferior izquierda de la Vista gráfica. Construcción de rectas paralelas y rectas perpendiculares 1. Abra Nueva ventana en GeoGebra. 2. Active la opción Recta 3. Con la opción Punto y trace una recta cualquiera. ubique un punto en el plano y denótelo con la letra M. Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio 4. Active la opción Paralela anteriormente. 5. Active la opción Perpendicular anteriormente. y haga click en el punto M y en la recta trazada y haga click en el punto M y en la recta trazada Construcción y medida de un ángulo 1. Abra Nueva ventana en GeoGebra. 2. Active la opción Punto , ubique un punto en el plano y denótelo con la letra O. 3. Active la opción Semirrecta punto O. y trace dos semirrectas distintas que partan del 4. Active la opción Ángulo y mida el ángulo haciendo click en un punto de una de las semirrectas, en el punto O y en un punto de la otra semirrecta. Gráfica de ecuaciones en el plano 1. Abra Nueva ventana en GeoGebra. 2. En la barra de entrada, escriba 𝑦 = 𝑥 y pulse ENTER. 3. Observamos que en la vista algebraica aparece la ecuación 𝑦 = 𝑥 y en la vista gráfica aparece la recta correspondiente. 4. Repita el paso 1 escribiendo en la barra de entrada 𝑦 = 𝑥 + 3 . 5. Observamos que en la vista algebraica aparece la ecuación 𝑦 = 𝑥 + 3 y en la vista gráfica aparece la recta correspondiente. Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio 6. Repita el paso 1 escribiendo en la barra de entrada 𝑦 = 𝑥^2 . 7. Observamos que en la vista algebraica aparece la ecuación 𝑦 = 𝑥^2 y en la vista gráfica aparece la parábola correspondiente. Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio Gráfica de funciones con diferentes dominios 1. Abra Nueva ventana en GeoGebra. 2. En la barra de entrada, escriba 𝑓(𝑥) = −3𝑥 + 1 y pulse ENTER. 3. Observamos que en la vista algebraica aparece la ecuación 𝑦 = 𝑥 y en la vista gráfica aparece la recta correspondiente. 4. En la barra de entrada, escriba la palabra Función y en el cuadro que aparece elija la opción Función(<Función>,<Valor inicial>,<Valor final>). En la barra de entrada aparece lo siguiente: Escriba 2x en Función, 0 en Valor inicial y 4 en Valor final, y de ENTER. 5. Observamos que en la vista algebraica aparece la ecuación 𝑓(𝑥) = 2𝑥, (0 ≤ 𝑥 ≤ 4) en la vista gráfica aparece la gráfica correspondiente. Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio Construcción de un deslizador 1. Abra Nueva ventana en GeoGebra. Elija la opción Deslizador y de click en cualquier lugar de la Vista gráfica. Se abre la caja de diálogo Deslizador. En la caja Deslizador cambie lo siguiente: el nombre del deslizador por 𝑏, en el intervalo coloque Mín: - 10 y Máx: 10, el incremento por 0.2 Pulse el botón OK para aceptar las modificaciones y salir. Observe los valores que toma 𝑏 deslizando el punto que aparece sobre el deslizador. Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio 2. En la barra de entrada, escriba 𝑦 = 𝑏 y pulse ENTER. 3. Mueva el punto que aparece sobre el deslizador 𝑏 y observe lo que pasa con la gráfica de la ecuación 𝑦 = 𝑏. Comente. 4. Repita el paso 2, cambiando el nombre del deslizador por 𝑛, el intervalo entre – 8 y 8 y el incremento por 1. Observe las los valores que toma 𝑛 deslizando el punto que aparece en el deslizador. 5. En la barra de entrada, escriba 𝑦 = 𝑛𝑥. 6. Mueva el punto que aparece sobre el deslizador 𝑛 y observe lo que pasa con la gráfica de la ecuación 𝑦 = 𝑛𝑥. Comente. Cambio de escala en los ejes coordenados 1. Abra Nueva ventana en GeoGebra. 2. Elija la opción Desplaza Vista Gráfica y arrastre el cursor sobre cada uno de los ejes coordenados. De esta manera se modifica la escala en cada eje según desee. Proyecto DGI-PUCP 2018-3-0051. Análisis de idoneidades en procesos de enseñanza y aprendizaje de las funciones afines y lineales, diseñados e implementados por profesores de secundaria en ejercicio