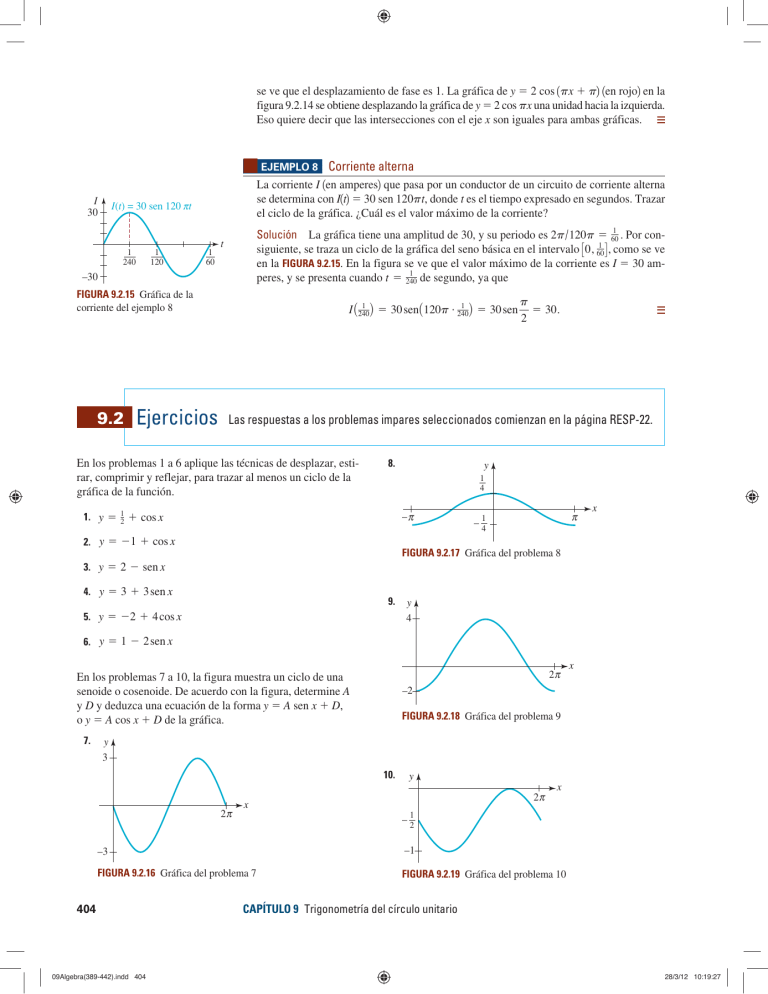
se ve que el desplazamiento de fase es 1. La gráfica de y 5 2 cos 1px 1 p2 1en rojo2 en la figura 9.2.14 se obtiene desplazando la gráfica de y 5 2 cos px una unidad hacia la izquierda. Eso quiere decir que las intersecciones con el eje x son iguales para ambas gráficas. ■ EJEMPLO 8 I 30 La corriente I 1en amperes2 que pasa por un conductor de un circuito de corriente alterna se determina con I1t2 5 30 sen 120pt, donde t es el tiempo expresado en segundos. Trazar el ciclo de la gráfica. ¿Cuál es el valor máximo de la corriente? I(t) = 30 sen 120 π t 1 240 1 120 1 60 Solución La gráfica tiene una amplitud de 30, y su periodo es 2p / 120p 5 601 . Por consiguiente, se traza un ciclo de la gráfica del seno básica en el intervalo C 0, 601 D , como se ve en la FIGURA 9.2.15. En la figura se ve que el valor máximo de la corriente es I 5 30 am1 peres, y se presenta cuando t 5 240 de segundo, ya que t –30 FIGURA 9.2.15 Gráfica de la corriente del ejemplo 8 9.2 Corriente alterna Ejercicios p 1 1 IA 240 B 5 30 sen A120p # 240 B 5 30 sen 5 30. 2 Las respuestas a los problemas impares seleccionados comienzan en la página RESP-22. En los problemas 1 a 6 aplique las técnicas de desplazar, estirar, comprimir y reflejar, para trazar al menos un ciclo de la gráfica de la función. 1. y 5 1 2 y 8. 1 4 –π 1 cos x 2. y 5 21 1 cos x π – 14 x FIGURA 9.2.17 Gráfica del problema 8 3. y 5 2 2 sen x 4. y 5 3 1 3 sen x 9. 5. y 5 22 1 4 cos x y 4 6. y 5 1 2 2 sen x 2π En los problemas 7 a 10, la figura muestra un ciclo de una senoide o cosenoide. De acuerdo con la figura, determine A y D y deduzca una ecuación de la forma y 5 A sen x 1 D, o y 5 A cos x 1 D de la gráfica. 7. x –2 FIGURA 9.2.18 Gráfica del problema 9 y 3 10. 2π x y 2π x – 12 –3 –1 FIGURA 9.2.16 Gráfica del problema 7 FIGURA 9.2.19 Gráfica del problema 10 404 09Algebra(389-442).indd 404 CAPÍTULO 9 Trigonometría del círculo unitario 28/3/12 10:19:27 En los problemas 11 a 16, use las relaciones 112 y 122 de la sección 9.2 para determinar las intersecciones con el eje x de la gráfica de la función indicada. No trace la gráfica. y 22. 2 11. y 5 sen px 12. y 5 2cos 2x 13. y 5 10 cos –1 x 2 x 3 –2 FIGURA 9.2.23 Gráfica del problema 22 14. y 5 3 sen 1 25x 2 p b 4 16. y 5 cos 1 2x 2 p 2 15. y 5 senax 2 y 23. 1 En los problemas 17 y 18, determine las intersecciones con el eje x de la gráfica de la función, en el intervalo 30, 2p4. A continuación, aplicando la periodicidad, determine todas las intersecciones. 17. y 5 21 1 sen x x –1 18. y 5 1 2 2 cos x En los problemas 19 a 24, la figura muestra un ciclo de una gráfica del coseno o seno. De acuerdo con la figura, determine A y B, y deduzca una ecuación de la forma y 5 A sen Bx o y 5 A cos Bx de la gráfica. 19. 1 –1 FIGURA 9.2.24 Gráfica del problema 23 y 24. 3 y 3 –4 x –3 x π 4 FIGURA 9.2.25 Gráfica del problema 24 –3 FIGURA 9.2.20 Gráfica del problema 19 En los problemas 25 a 32, determine la amplitud y el periodo de la función. Trace cuando menos un ciclo de la gráfica. 20. 25. y 5 4 sen px y 2 x π –2 26. y 5 25 sen FIGURA 9.2.21 Gráfica del problema 20 28. y 5 5 cos 4x 2 30. y 5 2 2 2 sen px 1 2 – 12 27. y 5 23 cos 2px 29. y 5 2 2 4 sen x y 21. x 2 2 31. y 5 1 1 cos x FIGURA 9.2.22 Gráfica del problema 21 2x 3 32. y 5 21 1 sen px 2 9.2 Gráficas de las funciones seno y coseno 09Algebra(389-442).indd 405 405 28/3/12 10:19:28 En los problemas 33 a 42, determine amplitud, periodo y desplazamiento de fase de la función. Trace al menos un ciclo de la gráfica. p 33. y 5 sen ax 2 b 6 34. y 5 sen a3x 2 35. y 5 cos ax 1 Aplicaciones diversas 51. Péndulo p b 4 El desplazamiento angular u de un péndulo, respecto a la vertical en el momento t segundos, se determina con u1t2 5 u0 cos vt, donde u0 es el desplazamiento inicial cuando t 5 0 segundos. Véase la FIGURA 9.2.26. Para v 5 2 rad/s y u0 5 p/10, trace dos ciclos de la función resultante. p b 6 37. y 5 4 cos a2x 2 3p b 2 38. y 5 3 sen a2x 1 p b 4 39. y 5 3 sen a 49. cos 1 x 1 p 2 5 2cos x 50. sen 1 x 1 p 2 5 2sen x p b 4 36. y 5 22 cos a2x 2 En los problemas 49 y 50, verifique gráficamente la identidad. p x 2 b 2 3 40. y 5 2cos a θ0 θ x 2 pb 2 p b 3 4p b 42. y 5 2 cos a22px 2 3 41. y 5 24 sen a x 2 p 3 FIGURA 9.2.26 Péndulo del problema 51 En los problemas 43 y 44, escriba la ecuación de la función cuya gráfica se describe en palabras. 52. Corriente En cierto circuito eléctrico, la corriente I, en amperes, cuando el tiempo es t, en segundos es I 1 t 2 5 10 cos a120 pt 1 43. La gráfica de y 5 cos x se estira verticalmente por un factor de 3, y a continuación se desplaza 5 unidades hacia abajo. Un ciclo de y 5 cos x en 30, 2p4 se comprime a 30, p/34 y el ciclo comprimido se desplaza p/4 unidades horizontalmente hacia la izquierda. 44. Un ciclo de y 5 sen x en 30, 2p4 se estira hasta 30, 8p4 y a continuación, el ciclo estirado se desplaza p/12 unidades horizontalmente hacia la derecha. La gráfica también se comprime verticalmente por un factor de 34, y a continuación se refleja en el eje x. En los problemas 45 a 48, determine las funciones seno y coseno, desplazadas horizontalmente, de manera que cada función satisfaga las condiciones dadas. Grafique las funciones. 45. Amplitud 3, periodo 2p/3, desplazada p/3 unidades hacia la derecha. 46. Amplitud 23 , periodo p, desplazada p/4 unidades hacia la Trace dos ciclos de la gráfica de I en función del tiempo t. 53. Profundidad del agua La profundidad d del agua, a la entrada de un puerto pequeño cuando el tiempo es t, se modela con una función de la forma d 1 t 2 5 A sen Bat 2 54. Temperatura Fahrenheit 47. Amplitud 0.7, periodo 0.5, desplazada 4 unidades hacia la izquierda. 406 09Algebra(389-442).indd 406 Suponga que T 1 t 2 5 50 1 10 sen 48. Amplitud 54 , periodo 4, desplazada 1/2p unidades hacia la p b 1 C, 2 donde A es la mitad de la diferencia entre las profundidades cuando las mareas son altas y bajas; 2p/B, B . 0, es el periodo de la marea y C es la profundidad promedio. Suponga que el periodo de la marea es de 12 horas, que la profundidad en la pleamar 1marea alta2 es de 18 pies, y que en la bajamar es de 6 pies. Trace dos ciclos de la gráfica de d. izquierda. derecha. p b. 3 p 1t 2 82, 12 0 # t # 24 es un modelo matemático de la temperatura Fahrenheit a las t horas después de medianoche, en cierto día de la semana. CAPÍTULO 9 Trigonometría del círculo unitario 28/3/12 10:19:30








