ÁNGULOS EN LA CIRCUNFERENCIA

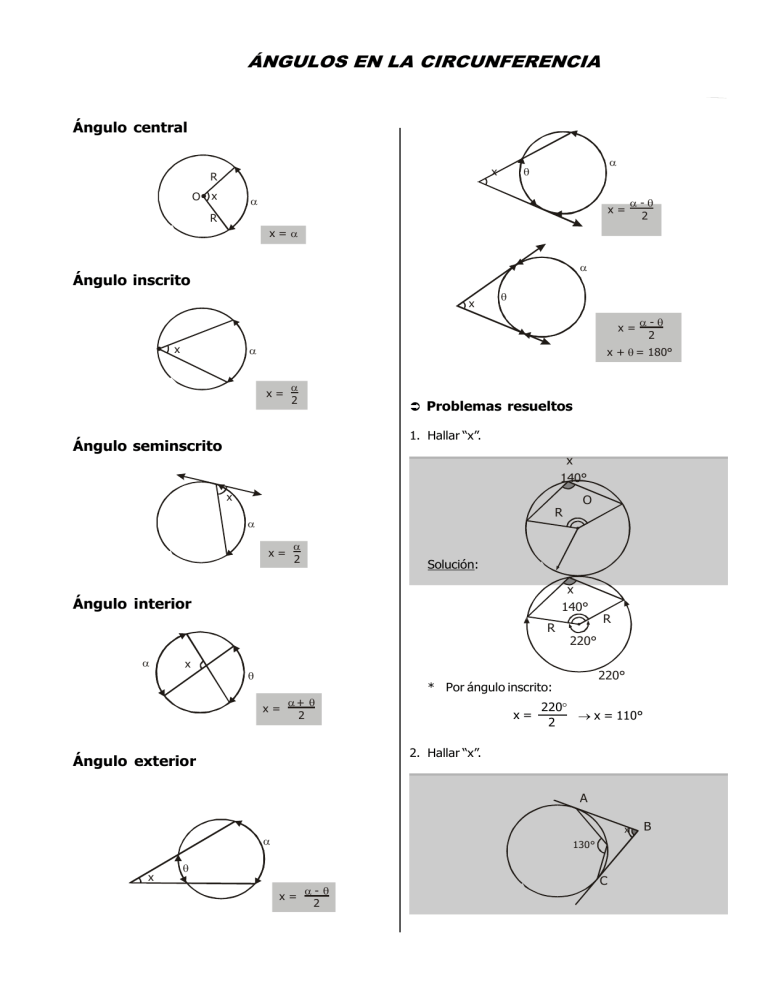
ÁNGULOS EN LA CIRCUNFERENCIA
Ángulo central
R
O x


x

x=
R
- 
2
x = 

Ángulo inscrito
x

x=
x

- 
2
x +  = 180°
x=

2
 Problemas resueltos
1. Hallar “x”.
Ángulo seminscrito
x
140°
x

x=

2
Solución:
x
Ángulo interior
140°
R

x
O
R

220°
220°
* Por ángulo inscrito:
x=
 
2
x=
R
220
 x = 110°
2
2. Hallar “x”.
Ángulo exterior
A
x

x
130°

x=
- 
2
C
B
Solución:
A
B
x
130°
260°
5. Si:  = 46°, hallar m BE . Además “P” y “Q” son puntos
de tangencia.
A
P

Q
C
* Del gráfico:
m AC = 360° - 260°  m AC = 100°
* Por ángulo exterior:
x + 100° = 180°  x = 80°
E
B
Solución:
2
P
A
46°
3. Hallar “x”.
Q
x
60° 40°
E
B
x
* Por ángulo interior:
2  x
2
2 + 92° = 2 + x  92° = x
 + 46° =
Solución:
A
x
E
Problemas de Aplicación
P
60° 40°
1. Hallar el valor de “x” siendo “O” el centro de la circunferencia.
B
*
A PB E :
B
x = 30° + 30° + 40°  x = 100°
A
x
O
80º
C
4. Hallar “x”, si: m APB = 140°.
A
x
a) 80º
d) 20º
B
P
b) 60º
e) 30º
c) 40º
2. Calcular “x”, si “B” y “D” son puntos de tangencia.
B
A
x
4x
C
Solución:
A
x


P
Q
D
a) 45º
d) 22º30’
 
B
b) 30º
e) 20º
c) 16º30’
3. Hallar “x”.
B
* En el
:
x +  +  +  +  = 360°
x + 2 + 2 = 360°
APBQ
x
x + 2( 

+
) = 360°
x + 2(140°) = 360°
x = 80°
20º
C
A
a) 50º
d) 80º
b) 60º
e) 40º
c) 70º
4. Hallar “x”.
a) 20º
d) 50º
A
P
x
M
B
a) 15º
d) 60º
b) 30º
e) 45º
c) 40º
10.Calcular “x”, si AD es diámetro.
N
b) 30º
e) 75º
C
B
x
C
42
A
c) 45º
D
E
5. En la figura el ángulo “A” mide 40º, hallar el ángulo “x”.
A
40º
a) 84º
d) 52º
N
M
a) 40º
d) 70º
c) 48º
11.En el gráfico “A”, “B”, “C” y “D” son puntos de tangencia.
Calcular “x”.
x
B
b) 46º
e) 44º
C
P
b) 20º
e) 80º
A
c) 30º
3x
80
B
a) 20º
d) 45º
x
A
70º
a) 100º
d) 90º
C
b) 30º
e) 50º
D
A
b) 110º
e) 70º
c) 80º
x
x
a) 100º
d) 120º
O
b) 155º
e) 130º
c) 150º
b) 110º
e) 135º
A
a) 80º y 30º
d) 110º y 50º
c) 15º
x
Q
b) 100º y 50º
e) 100º y 40º
c) 110º y 40º
14.En la figura, m AB - m CD = 18º. Calcular “x”.
B
C
9. Si: m BC = 100º, mAEB = 50º, hallar “x”. (“A” es punto
de tangencia).
C
35º
F
6
A
E
B
P
75º
3
A
c) 90º
13.En la figura mostrada, hallar los valores de los arcos AF
y PQ.
8. En la figura mostrada, calcular “ ”.
b) 12º
e) 20º
F
B
80º
a) 8º
d) 10º
c) 40º
12.En la figura, hallar “x”; FA y FB son tangentes;
F = 40º.
7. Calcular “x”, si “O” es centro.
a) 135º
d) 145º
40
C
D
6. En la figura calcular “x”.
60º
B
a) 30º
d) 6º
O
b) 4º
e) 8º
D
O1
c) 9º
x
15.En la figura “O” es centro; AB = CD. Calcular “x”.
C
B
b) 15
e) 15
c) 10
D
x
Autoevaluación
A
a) 30º
d) 60º
a) 20 u
d) 5
E
O
b) 45º
e) 53º
1. En la figura mostrada, calcular el valor de “x”.
C
B
c) 37º
16.En la figura mostrada BP es bisectriz, “P” es punto de
tangencia. Siendo: m FD = 36º; calcular el valor de “x”.
B
102º
2x
A
a) 58º
d) 80º
D
b) 68º
e) 39º
c) 78º
F
x
A
a) 40º
d) 20º
b) 36º
e) 18º
2. En la figura, calcular “x”, si “O” es centro, mAB = 45º;
además: EC = AO.
C
P
B
c) 30º
C
A
D
O
17. En la figura, calcular “”.
x
E
B
24º
A
a) 16º
d) 40º
a) 10º
d) 18º



b) 32º
e) 24º
C
c) 15º
3. Hallar “x”, si: mAB = 110º, “A” punto de tangencia.
A
c) 35º
18.Del gráfico, calcular “x”, (“A“ y “B” son puntos de
tangencia).
A
2x
60º
B
a) 80º
d) 70º
b) 12º
e) 21º
b) 60º
e) 50º
x
C
a) 10º
d) 6º
50º
b) 50º
e) 5º
B
c) 3º
4. Hallar “x - y”, si: RS // MN .
R
c) 40º
S
y
x
M
N
O
19.Calcular “x”, si “Q” es punto de tangencia.
B
A
a) 80º
d) 100º
P
x
Q
42º
C
b) 60º
e) 110º
5. Hallar “x + y”, si: AC = 2DE.
A
R
y
D
a) 48º
d) 84º
b) 96º
e) 88º
c) 90º
P
c) 90º
20.En un triángulo rectángulo, la suma de los catetos es
20 u. Calcular la suma de la circunferencia inscrita y el
radio de la circunferencia circunscrita.
D
40º
B
x
E
C
a) 50º
d) 80º
b) 60º
e) 90º
c) 70º
CUADRILÁTERO INSCRITO Y PUNTOS
NOTABLES EN EL TRIÁNGULO
Cuadrilátero inscrito en una circunferencia
Llamado también cuadrilátero cíclico, es aquel cuyos
vértices se encuentran ubicado s e n una misma
circunferencia.
B
Ejemplo: Los siguientes cuadriláteros son inscriptibles.
50º
100º
80º
50º
C
40º
A
D
40º
ABCD es un cuadrilátero inscrito
Propiedades del cuadrilátero inscrito
1. En todo cuadrilátero inscrito dos ángulos opuestos son
suplementarios.
1. Ortocentro.- Se llama así al punto de intersección de
las tres alturas de un triángulo. El ortocentro está ubicado
en:
* El interior de un triángulo si éste es acutángulo.
B

A
Puntos notables
C
O

D
+ = 180º
2. En todo cuadrilátero inscrito un ángulo interior es igual
a su opuesto exterior.

O  ortocentro
* El vértice del ángulo recto si es un triángulo
rectángulo.
O

 = 
O  ortocentro
3. En todo cuadrilátero inscrito el ángulo formado por un
lado con una diagonal es igual al que forman el lado
opuesto con la otra diagonal.

* El exterior de un triángulo si éste es obtusángulo.

 = 
O
O  ortocentro
Cuadrilátero inscriptible
Es aquel que puede ser inscrito en una circunferencia. Para
que un cuadrilátero sea inscriptible debe cumplir una de
las propiedades mencionadas.
2. Circuncentro.- Se llama así a la intersección de las
tres mediatrices de un triángulo. El circuncentro es el
centro de la circunferencia circunscrita.
* Si el triángulo es acutángulo, el circuncentro estará
ubicado en el interior del triángulo.
5. Excentro.- Se llama así al punto de intersección de
dos bisectrices exteriores y una bisectriz interior. El
excentro es el centro de la circunferencia exinscrita.
R
C
B
C  circuncentro
R circunradio
* Si el triángulo es rectángulo, el circuncentro estará
ubicado en el punto medio de la hipotenusa.
C
E
r


C


A


E  excentro relativo al lado BC.
r  exradio relativo al lado BC.
 Problemas resueltos
R
1. Si: AD = DC, hallar “x”.
C  circuncentro
R  circunradio
D
A
* Si el triángulo es obtusángulo, el circuncentro estará
ubicado en el exterior del triángulo.
x
B
C
C
Solución:
R
D
A
C  circuncentro
R  circunradio
45°
x
3. Baricentro.- Se llama así a la intersección de las tres
medianas de un triángulo. El baricentro divide a cada
mediana en dos segmentos que están en la relación de
dos a uno.
B
B
* En el
ABCD
C
inscriptible:
x = 45°
2. Hallar “x”.
x
2b
c
2a
a
G
2c
b
A
25°
C
Solución:
G  baricentro o gravicentro
4. Incentro.- Se llama así al punto de intersección de las
tres bisectrices interiores. El incentro es el centro de la
circunferencia inscrita.
x
B
C
 
A
I
I  incentro
r  inradio


r


*
ABCD
65°
25°
es inscriptible.
 x = 65°
D
Solución:
3. Hallar: m EB.
A
B
E
28°
P
B
Q
x
10°
x
H
40°
P
O
B
A
*
A
56°
O
*
62°
28°
x
F
E
x
B
Problemas de Aplicación
es inscriptible:
 m OEF = 28°
* En el AOE isósceles:
m AOE = 56°
* Luego:
x + 56° = 90°
 x = 34°
1. Calcular “x”.
x
4. Hallar “”, si “O” es el circuncentro del ABC.
B
6

3
C

150º
a) 20º
d) 30º
b) 70º
e) 15º
c) 40º
2. Si ABCD es un cuadrilátero inscriptible, calcular “x”.
B
O
Solución:
20º
C
x
B
A
C

A
D

O
2
a) 20º
d) 50º
b) 30º
e) 25º
c) 40º
3. De la figura, calcular “x”.
2
* Del gráfico:
3 = 360°
  = 120°
x
40º
5. Hallar “x”.
70º
B
x
a) 20º
d) 50º
H
A
80°
C
APQC
AOFE
A
40°
es inscriptible:
 m BPQ = 40°
* “H” es ortocentro del ABC:
 m ABH = 10°
* Luego:
x = 40° + 10°
 x = 50°
Solución:
28°
80°
40°
C
b) 30º
e) 60º
c) 40º
4. Si ABCD es un cuadrilátero inscriptible, calcular el valor
de “”.
B


A
50º
60º
a) 4 dm
d) 3
C
b) 25º
e) 55º
a) 36º
d) 45º
c) 35º
5. Calcular “x”; si ABCD es un cuadrilátero inscriptible,
AB = BC.
C
x
A
b) 15º
e) 30º
D
c) 20º
A
2x
B
3x
a) 18º
d) 12º
b) 24º
e) 15º
c) 54º
11.Si la hipotenusa de un triángulo rectángulo mide 12 m,
hallar la distancia del baricentro al ortocentro.
b) 3
e) 6
c) 4
12.En un triángulo la distancia del baricentro al circuncentro
es 8 m. Calcular la distancia del ortocentro al
circuncentro.
a) 14 m
d) 28
6. Si ABCD es un cuadrilátero inscriptible, calcular “x”.
D
c) 9
b) 72º
e) 56º
a) 2 m
d) 5
B
a) 10º
d) 25º
b) 8
e) 6
10.En un triángulo acutángulo el ángulo “B” mide 72° y su
ortocentro es “O”. Si: m AOC = 3, hallar el complemento
de “”.
D
a) 15º
d) 45º
9. En un triángulo rectángulo la hipotenusa mide 36 dm.
Hallar la distancia del baricentro al circuncentro.
b) 18
e) 34
c) 24
13.Si en un triángulo rectángulo la distancia del incentro a
la hipotenusa es 2 m, hallar la distancia del incentro al
ortocentro.
a) 0,5 m
b) 1
c) 1,5
d) 2 2
e) 3 2
C
14.Si “Q” es circuncentro, BÂC = 70°, hallar el ángulo
QBC.
c) 10º
B
7. Calcular m FMC.
B
M
A
a) 53º
d) 60º
Q
F
A
53º
b) 37º
e) 45º
C
c) 30º
a) 35º
d) 20º
C
b) 30º
e) 10º
15.Hallar “x”, si ABCD es un cuadrado.
B
8. Indicar verdadero o falso, según corresponda:
* El baricentro de un triángulo, es siempre un punto
interior a él.
* El circuncentro de un triángulo puede coincidir con
su ortocentro.
* En el triángulo rectángulo su ortocentro está en el
punto medio del lado mayor.
a) VVV
d) FVF
b) VFV
e) FFF
c) VVF
c) 25º
C
x
A
a) 40º
d) 70º
b) 50º
e) 80º
D
c) 60°
16.Si ABCD es un cuadrado, calcular “x”.
x
B
C
Autoevaluación
1. Siendo “P” circuncentro del triángulo ABC. Calcular
BÂC , si: BP̂C = 110°.
B
A
a) 30º
d) 53º
D
b) 45º
e) 60º
A
a) 35º
d) 65º
17. Calcular m AFE.
B
C
80º
70º
D
C
b) 45º
e) 75º
c) 55º
2. Siendo “O” ortocentro del triángulo ABC. Calcular AĈB ,
si: AÔB = 130°.
B
F
A
a) 120º
d) 150º
P
c) 37º
E
b) 105º
e) 140º
O
c) 135º
A
18.En el gráfico, calcular “x”.
a) 40º
d) 70º
C
b) 50º
e) 80º
c) 60º
3x
2x
3. En la figura mostrada QD es bisectriz; “D” es punto de
tangencia. Siendo: m R = 36º; calcular el valor del arco
EQ.
Q
a) 36º
d) 30º
b) 72º
e) 53º
c) 20º
E
P
19.En el gráfico, calcular “x”.
a) 60º
d) 20º
120º
x
b) 80º
e) 40º
b) 36º
e) 72º
C
D
c) 70º
A
20.Calcular “x”.
a) 45º
d) 30º
42º
c) 30º
4. Si “O” es centro, hallar “x”.
140º
a) 60º
d) 50º
R
D
b) 50º
e) 70º
75º
O
x
B
c) 60º
5. En el gráfico: m B = 62º; m C = 68º. Hallar la m AFD.
B
x
C
a) 42º
d) 60º
b) 48º
e) 70º
c) 30º
F
A
a) 120º
d) 130º
b) 100º
c) 135º
e) 150º
D