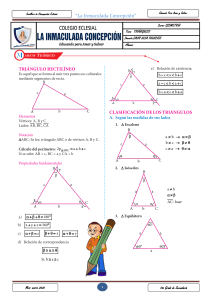
04 Triangulos I3ro
Anuncio

CEP. DIVINO REDENTOR 3º Secundaria Geometría B c x y a A CLASIFICACIÓN z I. C b Por la medida de sus lados. T. EQUILÁTERO T. ISÓSCELES Elementos: 60º Lados: a, b, c Vértices: A, B, C 60º ∡s INTERNOS: , , 60º Base ∡s EXTERNOS: x, y, z PERÍMETRO (2p) : a + b + c SEMIPERIMETRO (p) : p a b c T. ESCALENO 2 PROPIEDADES FUNDAMENTALES 1. + + = 180º 2. x=+ x 3. y z b T. Acutángulo T. Obtusángulo s Oblicuángulos x + y + z = 360º x 4. II. Por la medida de sus ángulos c T. Rectángulo b-c < a < b +c a Si: >> a>b>c 5. b 1º Bimestre Unidad 04 a c Unidad 04 3º Secundaria CEP. DIVINO REDENTOR PROBLEMAS PROPUESTOS Geometría 04. En la figura, si m∢A = m∢C + 30º calcular “x”. 01. En el gráfico, el triángulo ABC es equilátero. Calcular + + . 08. Hallar “x” A) 10º D) 30º B) 15º E) 35º C) 25º C 12. Hallar el gráfico “” B E B 6-50º +10 A A +30 A) 60 D) 110 x B B) 80 E) 120 C I +40 A) 145º D) 105º C C) 100 A) 30º D) 18º B) 135º C) 120º E) 100º B) 22º30’ C) 36º E) 15º A) 28 D) 31 B B 15+60º 10+40º 09. En la figura, calcular “x” 05. Hallar “x” si: AB = BC, BD = BE 02. Calcular m ∢ DBE según el gráfico mostrado. A F x B) 29 C) 30 E) N. A. 13. Hallar “x” x x 30º B E A x A D A) 30 D) 25 A D H A) 5 D) 45 C B) 15 E) 60 E B) 15 E) 19 C) 45 40º C A) 20º D) 90º B) 60º C) 80º E) 100º 06. Dos de los lados de un triángulo isósceles miden 9 y 19, entonces el perímetro del triángulo es: A) 37 D) 45 03. En el grafico, si m ∢BAC= 2m∢BCA, calcular “x”, os BI es bisectriz del ∢ABC. B) 40 E) 47 x A) 30º D) 75º 1º Bimestre B) 45º C) 60º E) N. A. A) C) 3 + 90º E) + 2 180º 46 B 120º 40º A A) 20º D) 50º B) 30º E) 60º D x C) 40º A D A) 10º D) 45º B) 15º E) 60º R 80º P B) + =90º D) 2+=180º x A C M Unidad 04 C C) 30º 15. En la figura, PB = BC y AP = PC calcular “x” B B x Q C) 60º 14. Según el grafico, si: AB = BD = DE = EC, calcular “x” C 11. En la figura si AB = BM y m∢A = 70º, hallar “x”. H C B) 70º E) 40º E P A 30º+ C) 50 07. Si en la figura PQ = QR, se cumple que: B A) 80º D) 50º 10. En el grafico, calcular “x” C C) 30 50º- D A 47 x C Unidad 04 3º Secundaria CEP. DIVINO REDENTOR A) 5º D) 20º 16. B) 10º E) 25º C) 15º Geometría 20. Siendo ABC un triángulo equilátero y m // n . Hallar “” En la figura. ¿Cuál es el segmento más pequeño?. B B 88º 6 73º D m 54º A C 44º A n A) 24 D) 18 C A) AB D) CD B) BC C) BD E) N. A. B) 28 C) 36 E) N. A. 21. En la figura, si aº + bº = 110º cº = 30º. Hallar “x” 17. Si L1 // L2. hallar “x” y bº x L1 2a x aº 110º a cº A) 28º D) 55º L2 B) 40º E) 70º C) 50º 22. Si x + y = 300. hallar “” A) 40 D) 100 B) 60 E) 120 C) 80 x 18. Si L1 // L2, hallar “x” L1 60º A) 20 D) 150º A) 100 D) 115 1º Bimestre B) 52 E) 50 B) 105 E) 120 C) 110 23. En la figura, calcular “x” L2 B) 130º C) 100º E) 160º x 19. En un triángulo ABC, AB = 10 y BC = 18. Si AC es el mayor valor par, entonces calcular el perímetro del triángulo ABC. A) 56 D) 54 y x x 60 A) 15 D) 30 C) 53 B) 20 E) 35 x C) 25 Departamento de Publicaciones “Divino Redentor” 48 Unidad 04 Unidad 04