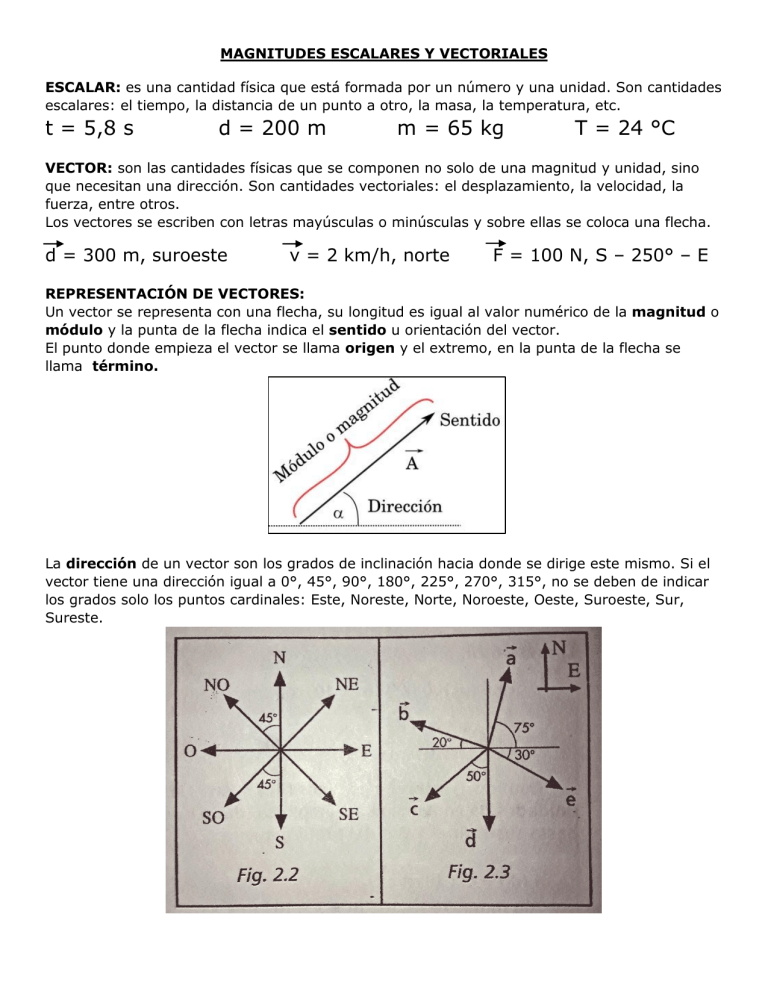
MAGNITUDES ESCALARES Y VECTORIALES ESCALAR: es una cantidad física que está formada por un número y una unidad. Son cantidades escalares: el tiempo, la distancia de un punto a otro, la masa, la temperatura, etc. t = 5,8 s d = 200 m m = 65 kg T = 24 °C VECTOR: son las cantidades físicas que se componen no solo de una magnitud y unidad, sino que necesitan una dirección. Son cantidades vectoriales: el desplazamiento, la velocidad, la fuerza, entre otros. Los vectores se escriben con letras mayúsculas o minúsculas y sobre ellas se coloca una flecha. d = 300 m, suroeste v = 2 km/h, norte F = 100 N, S – 250° – E REPRESENTACIÓN DE VECTORES: Un vector se representa con una flecha, su longitud es igual al valor numérico de la magnitud o módulo y la punta de la flecha indica el sentido u orientación del vector. El punto donde empieza el vector se llama origen y el extremo, en la punta de la flecha se llama término. La dirección de un vector son los grados de inclinación hacia donde se dirige este mismo. Si el vector tiene una dirección igual a 0°, 45°, 90°, 180°, 225°, 270°, 315°, no se deben de indicar los grados solo los puntos cardinales: Este, Noreste, Norte, Noroeste, Oeste, Suroeste, Sur, Sureste. La dirección de a es: E – 75° – N, que significa del este 75° hacia el norte. También podemos expresar esa dirección con el ángulo complementario de 75° que sería 15°. Entonces la dirección sería: N – 15° – E. Escriba las direcciones de los otros vectores en el cuadro que sigue: VECTOR DIRECCION DIRECCION COMPLEMENTARIA b c X d e Con frecuencia se utiliza otro criterio para dar direcciones. Se trata del modelo antihorario en donde solo se indican los grados a partir de 0° (en la posición donde va el Este) y en sentido contrario al giro de las manecillas del reloj. En la imagen anterior la dirección de p sería 50° Escriba las direcciones para los otros vectores en el cuadro que sigue: VECTOR a u k s DIRECCION TIPOS DE VECTORES: SUMA DE VECTORES SUMA DE VECTORES CONSECUTIVOS (método del polígono): cuando los vectores son consecutivos, al sumarlos su resultado es ( r ) que es un vector que se traza desde el origen del primer vector hasta el término del último vector. Trace el vector suma para los siguientes vectores consecutivos: m c a b b Figura 1 a Figura 2 n Figura 3 SUMA DE VECTORES CONCURRENTES (método del paralelogramo): para sumar vectores concurrentes con un origen común se traza una línea discontinua que pasa por el término de los vectores concurrentes que sean paralelas a ellos y formen la figura de un paralelogramo. Luego se traza una línea ( r ) por el medio que va desde el origen hasta el punto de intersección de las paralelas. Esta línea ( r ) representa la suma de los vectores concurrentes. f f f g g Trace el vector suma para los siguientes vectores concurrentes: r g




![1 Si v = [ 36 -12 ] , w = [ 9 -3 ] , y S = 1wl. Indique cuáles opciones](http://s2.studylib.es/store/data/004950498_1-7f0b4c506a631255d680bd90dfa0a3e5-300x300.png)



