modelaje bjt

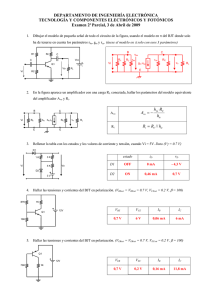
MODELAJE DEL BJT
INTRODUCCION.
Un modelo es la combinación de elementos de circuito, seleccionados
adecuadamente, que mejor aproximan el comportamiento real de un dispositivo
semiconductor en condiciones específicas de operación.
Por tanto, el equivalente de ca para una red se obtiene por medio de:
1. El establecimiento de todas las fuentes de cd a cero y su reemplazo por
un corto circuito equivalente.
2. El reemplazo de todos los capacitores por un corto circuito
equivalente.
3. La eliminación de todos los elementos sustituidos por los corto
circuitos equivalentes introducidos en los pasos 1 y 2.
4. El dibujar de nuevo la red en una forma más lógica y conveniente.
Por ejemplo:
Vcc
RB
B
RC
vi
C vo
vi
RB
Circuito
Equivalente
E
C
vo
RC
B
E
(a)
(b)
Ejemplo. En (a) Circuito normal y en (b) modelo equivalente.
Los detalles que faltan para poder realizar un modelo apropiado para un
análisis de pequeña señal se detallan a continuación.
1
PARAMETROS IMPORTANTES: ZI, ZO, AV, AI. (REDES DE DOS PUERTOS).
Reacuérdese del apunte de cuadripolos los sistemas de 2 puertos.
ii
i0
Sistema de dos puertos
+
Vi
Salida
Entrada
+
Vo
-
Zi
Zo
Figura 1. Sistema de dos puertos.
Los parámetros de principal importancia para un amplificador son la
impedancia de entrada Zi, la impedancia de salida Zo, la ganancia de voltaje Av, la ganancia
de corriente Ai y las relaciones de fase resultantes. Otros factores, tales como la frecuencia
aplicada para los límites inferior y superior del espectro de frecuencias, afectarán algunos
de estos parámetros
Impedancia de entrada, Zi
Para el extremo de entrada, la impedancia de entrada Z¡ se define por la
ley de Ohm como se indica a continuación:
Zi =
Vi
Ii
Para el análisis de pequeña señal una vez que se ha determinado la
impedancia de entrada, el mismo valor numérico puede utilizarse para modificar los niveles
de la señal aplicada.
La impedancia de entrada de un amplificador de transistor BJT es de
naturaleza puramente resistiva y, dependiendo de la manera en que se emplee el transistor,
puede variar de unos cuantos ohms hasta el orden de los megaohms.
2
Impedancia de salida, Zo
La impedancia de salida se define en forma natural para el conjunto de
salida de las terminales, pero la manera en la cual se define es bastante diferente de la
correspondiente a la impedancia de entrada. Es decir, la impedancia de salida se determina
en las terminales de salida viendo hacia atrás. Dentro del sistema con la señal aplicada
fijada en cero.
V
Zo = o
Io
En particular, para las frecuencias de rango bajo y medio (normalmente <
100 kHz): La impedancia de salida de un amplificador de transistor BJT es resistiva por
naturaleza y depende de la configuración y de la colocación de los elementos resistivos, Zo
puede variar entre unos cuantos ohms y un nivel que puede exceder los 2MΩ .
Ganancia de voltaje, Av
Una de las características más importantes de un amplificador es la
ganancia de voltaje de pequeña señal de ca, que se determina por
Av =
Vo
Vi
Para amplificadores de transistor, la ganancia de voltaje sin carga es mayor
que la ganancia de voltaje con carga.
Ganancia de corriente, Ai
La última característica numérica por discutir es la ganancia de corriente
definida por
AI =
Io
Ii
Aunque por lo regular recibe menos atención que la ganancia de voltaje,
es, sin embargo, una cantidad importante que puede tener un impacto significativo en la
eficiencia global de un diseño. En general:
Para amplificadores BJT, la ganancia de corriente oscila entre los valores
apenas menores que I y un nivel que puede exceder los 100.
3
Relación de fase
La relación de fase entre las señales senoidales de entrada y salida es
importante por una variedad de razones prácticas. Sin embargo y por fortuna: Para el
amplificador de transistor típico, a frecuencias que permiten ignorar el efecto de elementos
reactivos, las señales de entrada y salida están ya sea en fase o desfasadas por 180°.
EL MODELO EQUIVALENTE HIBRIDO.
El resultado es una resistencia de entrada que variará en el punto de
operación de cd. Para el modelo equivalente híbrido que se describirá se definen los
parámetros en un punto de operación que puede o no reflejar 1as condiciones de operación
reales del amplificador. Esto se debe al hecho de que las hojas de especificaciones no
pueden proporcionar los parámetros para un circuito equivalente para todo punto de
operación posible. Los fabricantes deben escoger las condiciones de operación que creen
que reflejarán las características generales del dispositivo.
La descripción del modelo híbrido equivalente se principia con la relación
directa con las redes de dos puertos de la figura 1. El siguiente conjunto de ecuaciones
muestra la relación.
Vi = h11 I i + h12Vo
I o = h21 I i + h22Vo
De estas ecuaciones se desprenden los parámetros híbridos que vemos a
continuación.
h11 =
Vi
Ii
Ω
Vo =0
Este parámetro se llama “parámetro de impedancia de entrada a
cortocircuito”.
h12 =
Vi
Vo
sin unidad
I i =0
Este parámetro se llama “parámetro de la relación de voltaje de
transferencia inversa a circuito abierto”.
h21 =
4
Io
Ii V
sin unidad
o
=0
Este parámetro se llama “parámetro de la relación de transferencia directa
de corriente a corto circuito”.
h22 =
Io
Vo
siemens
I i =0
Este parámetro se llama “parámetro de admitancia de salida a circuito
abierto”.
El circuito equivalente ac completo para el dispositivo lineal básico está
mostrado en la figura 2, junto con un nuevo conjunto de subíndices para los parámetros h.
la naturaleza de la notación es práctica. La elección de las literales es obvia a partir del
siguiente listado:
h11→ resistencia de entrada (input) → hi
h11→ relación de voltaje de transferencia inversa (reverse) → hr
h11→ relación de corriente de transferencia directa (foward) → hf
h11→ conductancia de salida (output) → ho
Ii
IO
hi
+
+
Vi
+
hrVo
-
hfIi
ho
-
VO
-
Figura 2. Circuito equivalente híbrido completo.
Ejemplo de aplicación se ve en la siguiente figura:
Ib
Ic
Ib
b
Vbe
-
Vce
hreVce
hfeIb
hoe
-
+
Vbe
E
c
+
C
+
B
+
Ic
hie
-
+
Ie
-
Vce
e
Figura 3. Circuito híbrido equivalente para la
configuración emisor común
5
El nuevo subíndice “e” se debe a la configuración de emisor común. Para
las configuraciones de colector común y base común la nomenclatura es hic, hrc, hfc, hoc,
y hib, hrb, hfb, hob, respectivamente. Existen tablas para obtener con cálculo simple los
diferentes parámetros h en distintas configuraciones.
DETERMINACION GRAFICA DE LOS PARAMETROS “h”.
Mediante el uso de derivadas parciales, se puede mostrar la magnitud de
los parámetros h para el circuito equivalente de pequeña señal del transistor en la región de
operación para la configuración en emisor común puede encontrarse a través de las
siguientes ecuaciones:
hie =
hre =
h fe =
hoe =
∂vi ∂vbe ∆vbe
=
≅
∂ii
∂ib
∆ib
VCE = cons
∂vi ∂vbe ∆vbe
=
≅
∂vo ∂vce ∆vce
I B = cons
∂io ∂ic ∆ic
=
≅
∂ii ∂ib ∆ib
VCE = cons
∂io ∂ic
∆i
=
≅ c
∂vo ∂vo ∆vce
I B = cons
En cada caso el símbolo ∆ se refiere a un pequeño cambio en la cantidad
alrededor del punto de operación estable.
Los parámetros hie y hre están determinados a partir de las características
de entrada o de base, mientras que los parámetros hfe y hoe se obtienen desde la salida o de
las características del colector.
Procedimiento:
El primer paso para calcular cualquiera de los parámetros híbridos
consiste en encontrar el punto de operación estable.
Para obtener el hfe la condición VCE = constante requiere que los
cambios en la corriente de la base y en la corriente del colector se
hagan a lo largo de una línea vertical dibujada a través del punto Q
que representa el voltaje colector emisor fijo.
Se deben obtener los deltas de variación que deben ser pequeños
para lograr exactitud.
6
Veamos con la figura 4 lo que hemos planteado y obtengamos un
pequeño ejemplo numérico:
IC (mA)
+60µA
7
+50µA
6
+40µA
5
+30µA
4
IB = +20µA
3
Recta de carga
1
0
IB = +10µA
Q
∆ic 2
5
10
IB = 0µA
15
20
VCE (V)
VCE = 8.4V
Figura 4. Determinación de hfe.
Reemplazando valores de la figura a la ecuación de hfe
h fe =
∆ic
∆ib
=
VCE = cons
(2.7 − 1.7)mA
= 100
(20 − 10) µA VCE =8.4V
Para obtener el hoe se traza una línea recta tangente a la curva de IB
a través del punto Q para establecer una línea en IB = constante.
Se deben obtener los deltas de variación que deben ser pequeños
para lograr exactitud.
Veamos con la figura 5 lo que hemos planteado y obtengamos un
pequeño ejemplo numérico:
7
IC (mA)
+60µA
7
+50µA
6
+40µA
5
+30µA
4
+20µA
3
IB = +15µA
Q
∆ic 2
+10µA
IB = 0µA
1
0
5
7
∆vce
10
15
20
VCE (V)
Figura 5. Determinación de hoe.
Reemplazando valores de la figura a la ecuación de hoe
hoe =
∆ic
∆vce
=
Ij B = cons
(2.2 − 2.1)mA
= 33µS
(10 − 7)V I B =15 µA
Para determinar los parámetros hie y hre primero debe encontrarse
el punto Q sobre la entrada o las características de base.
Para hie se dibuja una línea tangente a la curva en VCE = 8.4V a
través del punto Q Para establecer una línea en VCE = constante.
Se deben obtener los deltas de variación que deben ser pequeños
para lograr exactitud.
Veamos con la figura 6 lo que hemos planteado y obtengamos un
pequeño ejemplo numérico:
8
IB (mA)
VCE = 0V
VCE = 10V
30
VCE = 20V
VCE = 8.4V
20
∆ib = 10µA
15
10
0.6
0.7
0.8
VBE (V)
∆vbe = 0.015V
Figura 6. Determinación de hie.
Reemplazando valores de la figura a la ecuación de hie
hie =
∆vbe
∆ib
=
VCE = cons
(733 − 718)mV
(20 − 10) µΑ
= 1.5kΩ
VCE =8.4V
El ultimo parámetro, hre se puede encontrar al dibujar una línea
horizontal a través del punto Q en IB = 15µA.
Se deben obtener los deltas de variación que deben ser pequeños
para lograr exactitud.
Veamos con la figura 7 lo que hemos planteado y obtengamos un
pequeño ejemplo numérico:
9
IB (mA)
VCE = 0V
VCE = 10V
30
VCE = 20V
20
Q
15
IB = 15µA
10
0.6
0.7
0.8
VBE (V)
∆vbe = 0.008V
Figura 7. Determinación de hre.
Reemplazando valores de la figura a la ecuación de hre
hre =
10
∆vbe
∆vce
=
I B = cons
(733 − 725)mV
= 4 *10 − 4
(20 − 0)V
CONVERSION ENTRE PARAMETROS.
Tabla 1. Conversión de parámetros “h”
Emisor Común
hie
Colector Común
Base común
hic
hib
1 + h fb
hie hob
− hrb
1 + h fb
hie
hre
hre
1 − hrc
h fe
h fe
− (1 + h fc )
hoe
hoe
hoc
hob
1 + h fb
hic
hie
hic
hib
1 + h fb
hrc
1 − hre
hrc
1
h fc
− (1 + h fe )
h fc
hoc
hoe
hoc
hib
hrb
−
hie
1 + h fe
hie hoe
− hre
1 + h fe
h fb
−
h fe
1 + h fe
hob
−
hoe
1 + h fe
−
−
h fb
1 + h fb
1
1 + h fb
hob
1 + h fb
hib
hic hoc
−1
h fc
hrb
1 + h fc
h fc
h fb
hoc
h fc
hob
hrc −
−
hic
h fc
−
−
11
Ejemplo.
Dibuje el modelo de pequeña señal del siguiente circuito.
Vcc
R1
RC
vo
vi
R2
RE
Figura 8. Circuito con polarización universal.
R: Siguiendo los pasos indicados en este apunte y tomando en cuenta el
modelo híbrido del transistor, obtenemos lo siguiente.
hie
vi
R1
R2
vCEhre
ibhfe
hoe
RE
Figura 9. Modelado del circuito de la figura 8.
12
RC
vo