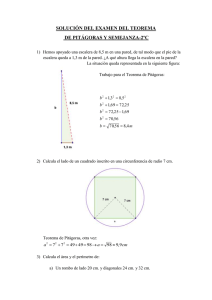
Tipo de reactivo: Composición. CAMPO DISCIPLINAR: Matemáticas. ASIGNATURA: Trigonometría. Grado escolar: 2018, tercer semestre. Reactivos de respuesta restringida Nivel cognitivo: Aplicación, análisis Instrucciones: En este reactivo deberás contestarlo con bolígrafo, sin tachaduras o enmendaduras para evitar malos entendidos o confusiones. Tu letra debe ser clara, legible y tu respuesta redactada sin faltas de ortografía, de manera que tú y yo entendamos lo mismo que quieres decir. En caso de no cumplir con alguno de estos aspectos, tu respuesta no podrá ser evaluado, debiendo ser corregida de acuerdo como se te indique. ¿Cuáles son las diferencias de aplicación de las razones trigonométricas y el teorema de Pitágoras? considerando que ambos se usan en un triángulo rectángulo. Tiene un valor de 10 puntos si consideras a las razones trigonométricas: Sen A= CO/H; Cos A = CA/H; Tan = CO/CA y para el teorema de Pitágoras es: c2 = a2 + b2; a2 = c2 – b2; b2 = c2 – a2. Tiene un valor de 5 puntos si consideras dos de las razones trigonométricas: Sen A= CO/H; Cos A = CA/H; Tan = CO/CA y dos del teorema de Pitágoras: c2 = a2 + b2; a2 = c2 – b2; b2 = c2 – a2. Tiene un valor de 2 puntos si consideras al menos una de las razones trigonométricas: Sen A= CO/H; Cos A = CA/H; Tan = CO/CA y una del teorema de Pitágoras: c2 = a2 + b2; a2 = c2 – b2; b2 = c2 – a2. Reactivos objetivos Reactivo de complementación. Instrucción. Escribe tus respuestas en las líneas que aparecen al final de cada enunciado. Su escritura debe ser legible, utilizando bolígrafo de tinta negra o azul y sin faltas de ortografía, en caso contrario, su respuesta no tendrá derecho a ser evaluada por que no cumple los requisitos. Complementación 1. En la solución de un binomio al cuadrado, se obtiene como resultado un trinomio ____________________. Canevá. 2. La regla para resolver un ________________ cuadrado perfecto es: cuadrado del ________________ término, más ______________ del primer término por el segundo término, más el _________________ del segundo término. Tipo de reactivo: Objetivos. CAMPO DISCIPLINAR: Matemáticas. ASIGNATURA: Pensamiento algebraico y de funciones. Grado escolar: 2018, segundo semestre. Reactivos de opción múltiple Nivel cognitivo: Aplicación, análisis. Instrucciones: * Solo puedes hacer uso de lápiz, goma y bolígrafo. * Justifica la respuesta de cada pregunta, en caso de no tener justificación no será correcto el reactivo. * Escribe con lápiz de forma clara, ordenada y fácil de leer, utiliza el espacio en blanco y la parte posterior para el procedimiento. * El resultado y el inciso escríbelo con bolígrafo. * El copiar, reemplazar a otra persona o hacer trampa se sancionará por lo menos con calificación reprobatoria. * Valor total del examen 100% La ecuación que representa a la siguiente expresión de forma simplificada, es: ---------------------------------------------------------- ( ) (3𝑥 + 7) = −1(2𝑥 2 − 5𝑥 + 6) A) 2𝑥 2 − 2𝑥 + 13 = 0 B) −2𝑥 2 + 8𝑥 + 1=0 C) 𝑥 2 − 𝑥 + 6=0 D) 𝑥 2 + 3𝑥 − 4=0 1.- Si hemos recorrido 21 km, que son las tres séptimas partes del trayecto, ¿cuántos kilómetros quedan por recorrer? ---------- ( A) 20 km B) 24 km C) 28 km D) 26 km ) Tipo de reactivo: Objetivos. CAMPO DISCIPLINAR: Matemáticas. ASIGNATURA: Pensamiento algebraico y de funciones. Grado escolar: 2018, segundo semestre. Reactivos de opción múltiple Nivel cognitivo: Aplicación, análisis. ( ) Expresión que representa, un terreno rectangular que tiene 120 metros de perímetro. ( ) La suma de dos números reales es 30 ( ) Tiene cuatro cuadrantes ( ) A (- 6, - 5) pertenece al cuadrante ( ) La solución de esta ecuación −3𝑥 + 4 = −1 es: A) Las coordenadas B) 120 = 2a + 2b C) X = 5/3 D) x8 - 36 3+5𝑥 E) X= 0 4−𝑥 F) Plano cartesiano ( ) La solución de esta ecuación ( ) La solución de esta ecuación, 5𝑥 − 4 = 2(𝑥 − 2) es: H) X = -1/40 ( ) La solución del binomio al cuadrado (2x + y)2 = es: I) Tercero ( ) La solución de los binomios conjugados (x4 + 6) (x4 - 6) = es: J) X + y =30 ( ) La factorización de 4x2 – 81 = es: K) 4x2 + 4xy + y2 5 = 7 es: G) (2x + 9)(2x – 9)