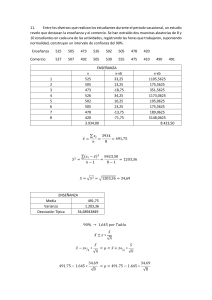
Modelo Logit y Adquisición de Automóviles: Análisis Econométrico
Anuncio

a) Interprete el modelo logit estimado. Observe que aquí el registro de la razón de posibilidades es una función del registro de ingresos, por lo que es un modelo de registro doble. Por lo tanto, si el ingreso aumenta en un 1%, en promedio, el registro de las probabilidades a favor de ser propietario de una casa aumenta en aproximadamente un 34.75%. b) Del modelo logit estimado, ¿cómo obtendría la expresión para la probabilidad de adquirir un automóvil? Tomando el antilog de la ecuación estimada, obtenemos: 𝑃𝑖 = 0.0625𝑋 0.3475 (1 − 𝑃𝑖) Donde X es el ingreso, se tiene que comprobar que el registro de esta expresión se obtiene de la ecuación dada en la pregunta. Obtenemos la expresión de la probabilidad de la siguiente manera: 𝑃𝑖 = 0.0625𝑋 0.3475 1 + 0.0625𝑋 0.3475 c) ¿Cuál es la probabilidad de que una familia con un ingreso de $20 000 posea un automóvil?, ¿y para un nivel de ingreso de $25 000? ¿Cuál es la tasa de cambio de la probabilidad en un nivel de ingreso de $20 000? Esta probabilidad es: 𝑷𝒊 = 𝟎. 𝟎𝟔𝟐𝟓(𝟐𝟎𝟎𝟎)𝟎.𝟑𝟒𝟕𝟓 = 𝟎. 𝟔𝟔 𝟏 + 𝟎. 𝟎𝟔𝟐𝟓(𝟐𝟎𝟎𝟎)𝟎.𝟑𝟒𝟕𝟓 Es decir, la probabilidad es de 66 % aproximadamente. Por lo tanto, cuando el nivel de ingresos de 25.000 la probabilidad de tener un automóvil es de 68 %. d) Comente sobre la significancia estadística del modelo logit estimado. Desde los resultados dados se puede ver que los coeficientes son individualmente muy significativos y que el valor de X2, tiene una medida de bondad de ajuste, también es estadísticamente significativa. a) Con el modelo MLP, prediga la probabilidad de admisión al programa con base en las calificaciones cuantitativas y verbales del GRE. Los resultados de la MLP modelo son los siguientes: Yt = -2.867329 + 0,003126 + 0.002343 ^ t = (-3.422404) (2,975812 ) (3,440517 Donde Y = 1 si es admitido al programa de posgrado; de lo contrario, 0 b) ¿Es un modelo satisfactorio? De no ser así, ¿qué alternativa(s) ofrece? Aunque los resultados estadísticos parecen satisfactorios, el MLP no es un buen modelo debido a los problemas discutidos en clase, a, la no normalidad del término de error, la heterocedasticidad, etc.