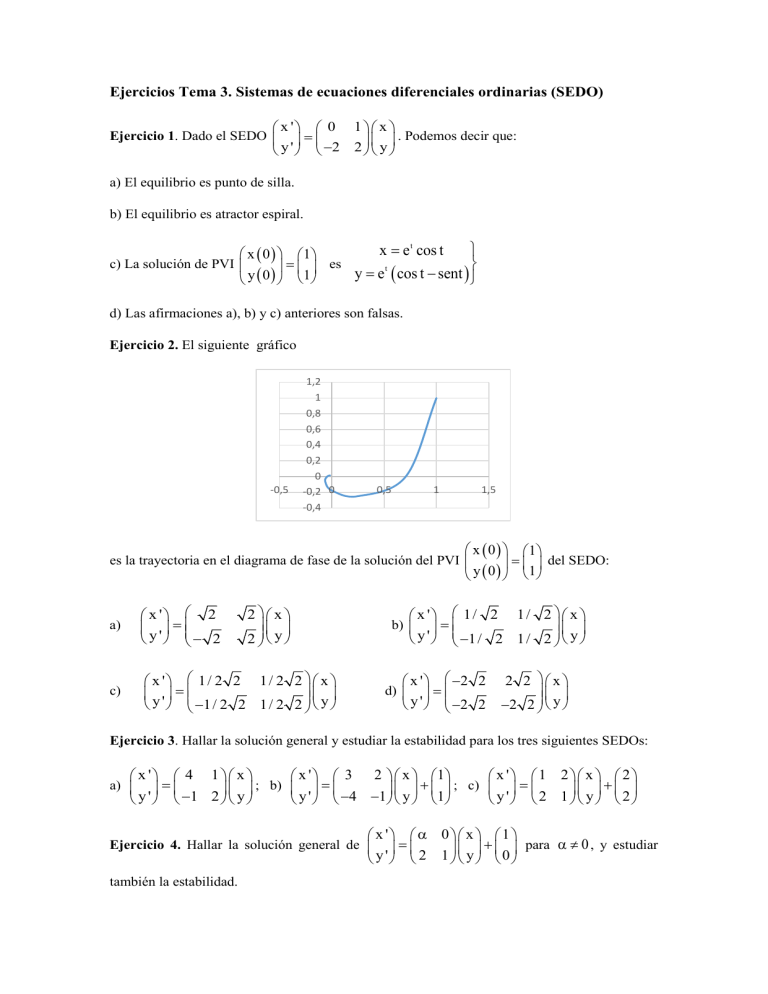
Ejercicios Tema 3. Sistemas de ecuaciones diferenciales ordinarias (SEDO) x ' 0 1 x Ejercicio 1. Dado el SEDO = . Podemos decir que: y ' −2 2 y a) El equilibrio es punto de silla. b) El equilibrio es atractor espiral. x = e t cos t x ( 0 ) 1 c) La solución de PVI = es t y e ( cos t − sent ) y ( 0 ) 1 = d) Las afirmaciones a), b) y c) anteriores son falsas. Ejercicio 2. El siguiente gráfico -0,5 1,2 1 0,8 0,6 0,4 0,2 0 -0,2 0 -0,4 0,5 1 1,5 x ( 0 ) 1 = del SEDO: y ( 0 ) 1 es la trayectoria en el diagrama de fase de la solución del PVI a) x ' 2 = y ' − 2 2 x 2 y c) x ' 1/ 2 2 1/ 2 2 x = y ' −1/ 2 2 1/ 2 2 y x ' 1/ 2 1/ 2 x = y ' −1/ 2 1/ 2 y b) x ' −2 2 = y ' −2 2 d) 2 2 x −2 2 y Ejercicio 3. Hallar la solución general y estudiar la estabilidad para los tres siguientes SEDOs: x ' 4 1 x x ' 3 2 x 1 x ' 1 2 x 2 ; c) = = ; b) + = + y ' −1 2 y y ' −4 −1 y 1 y ' 2 1 y 2 a) x ' α 0 x 1 + para α ≠ 0 , y estudiar y ' 2 1 y 0 Ejercicio 4. Hallar la solución general de = también la estabilidad.










