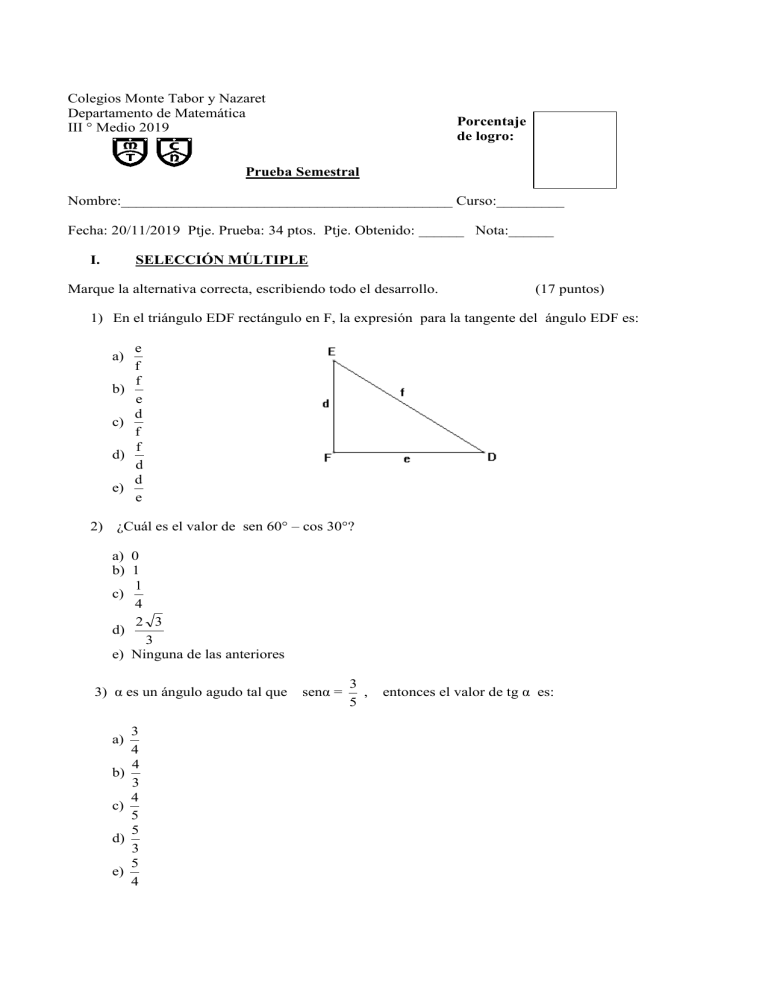
Colegios Monte Tabor y Nazaret Departamento de Matemática III ° Medio 2019 Porcentaje de logro: Prueba Semestral Nombre:____________________________________________ Curso:_________ Fecha: 20/11/2019 Ptje. Prueba: 34 ptos. Ptje. Obtenido: ______ Nota:______ SELECCIÓN MÚLTIPLE I. Marque la alternativa correcta, escribiendo todo el desarrollo. (17 puntos) 1) En el triángulo EDF rectángulo en F, la expresión para la tangente del ángulo EDF es: a) b) c) d) e) e f f e d f f d d e 2) ¿Cuál es el valor de sen 60° – cos 30°? a) 0 b) 1 1 c) 4 2 3 d) 3 e) Ninguna de las anteriores 3) α es un ángulo agudo tal que senα = a) b) c) d) e) 3 4 4 3 4 5 5 3 5 4 3 , 5 entonces el valor de tg α es: 4) Un ratón observa a un águila en la copa de un árbol con un ángulo de elevación de 70°. Si la distancia del ratón al árbol es 12 m, determinar la distancia entre el águila y el ratón. 12 tan 70º 12 B) cos 70º 12 C) sen 70º cos 70º D) 12 sen 70º E) 12 A) 5) ¿Cuánto suman las soluciones de la ecuación 2x2 – 4x + 9 = 0? a) b) c) d) e) –2 1 2 4 4,5 6) ¿Cuánto debe valer k para que las soluciones de la ecuación x2 – (k + 1)x + k = 0 sean reales e iguales? a) b) c) d) e) –1ó1 0 1 2 ó –2ó2 2 7) Si x1 y x2 son soluciones de la ecuación 2x2 + m = 5mx + 1 y x1 es el inverso multiplicativo de x2, entonces el valor de m es: a) b) c) d) e) 1 2 3 4 5 8) Si la ecuación x2 + px + q = 0 tiene dos raíces reales e iguales de valor –3, entonces p + q vale: a) b) c) d) e) –6 0 3 6 15 9) El punto (1, –1) pertenece a la gráfica de la función cuadrática f(x) = ax2 – 2x, entonces el valor de a es: a) b) c) d) e) –3 –2 –1 1 2 10) Si f(x) = x 2 – 6kx + 11 y f(1) = 0 , entonces el valor de k es: a) b) c) d) e) –2 1 2 6 11 11) ¿Cuál es el valor máximo que alcanza la función f(x) = – x2 – 6x + 1? a) – 26 b) – 3 c) 3 d) 10 e) 28 12) Con respecto a la función f(x) = x2 – 4x + 6, se puede afirmar que: I) Corta al eje X en dos puntos II) Corta al eje Y en (0,6) III) Su vértice tiene abscisa – 2 a) b) c) d) e) Sólo II Sólo III Sólo I y II Sólo II y III Ninguna de ellas 13) El gráfico, corresponde a la función definida por: a) b) c) d) e) y y y y y = = = = = x2 – 6x + 5 x2 + 6x + 5 x2 + 5 x2 + 6x x2 – 6x 14) ¿Para qué valor(es) de x la parábola de ecuación y = 2x2 – 5x + 3 intersecta al eje X? a) 1 b) 3 3 c) 2 d) 3 y 1 3 e) y 1 2 15) La hipotenusa de un triángulo rectángulo es igual a 34 cm. Sabiendo que un cateto es 14 cm mayor que el otro, la ecuación que permite resolver el problema es: a) b) c) d) e) x2 – 342 = (x +14)2 x2 + 342 = (x +14)2 x2 = (x +14)2 + 342 342 + (x +14)2 = x2 342 – x2 = (x +14)2 16) La trayectoria de un proyectil está dada por la función g(t) = 100t – 5t 2 , donde el tiempo “t” se mide en segundos y la distancia g(t) se mide en metros. ¿A los cuántos segundos estará el proyectil a 420 metros sobre el nivel del suelo? I) a) b) c) d) e) 6 segundos II) 10 segundos III) 14 segundos Sólo I Sólo II Sólo III Sólo I y II Sólo I y III 17) Al observar el siguiente grafico de una función cuadrática de la forma f (x ) ax 2 bx c , se puede deducir que I) c 0 II) a 0 III) b 2 4ac 0 a) Solo I b) Solo II c) Solo III d) Solo I y II e) Solo II y III II) Desarrollo Para la siguiente función cuadrática f(x) = 2x2 + x - 6 determina: La ausencia de desarrollo correspondiente anulará tu respuesta. a) Concavidad (0.5 pto) b) Intersección con eje Y (0.5 pto) c) Intersecciones con eje X (2 ptos) d) Vértice (1pto) e) Eje de simetría (1 pto) f) Dominio y recorrido (1pto) g) Gráfico (1 pto) 2) Para los siguientes problemas plantea y resuelve la ecuación asociada a cada problema: a) Una persona sube por un camino que tiene 30º de pendiente respecto del plano horizontal. Al cabo de caminar 500 metros, ¿a qué altura sobre el plano horizontal se encuentra la persona? (2 ptos) Resp.________________________________________________________________________ b) Calcula el radio de un círculo sabiendo que si aumentamos el radio en 6 cm, el área se hace nueve veces más grande. (2 puntos) Respuesta:______________________________________________________________________ c) El área de un rectángulo es 600 cm2. Calcula las dimensiones del rectángulo sabiendo que su perímetro es 100 metros. (2 puntos) Respuesta:_______________________________________________________________________ 3) Un cohete de juguete se lanzó al aire desde el techo de un granero. Su altura (h) en metros está dada por la función h(t)= −2t2+4t+16 después de t segundos de haber sido lanzado.(4 puntos) a) ¿Cuánto tiempo transcurre hasta que el cohete alcance su altura máxima? b) ¿Qué altura máxima alcanzó el cohete? c) ¿Cuánto tiempo estuvo el cohete en el aire antes de llegar al suelo? d) ¿En qué momento o momentos estará el cohete a una altura de 16 metros? Punto extra: Un agricultor debe cercar en forma rectangular un pedazo de un potrero. Para ello compró 4.000 metros de alambre de púas que debe disponer en cuatro líneas como se muestra en la siguiente imagen: ¿Cuáles deben ser las dimensiones del terreno a cercar para que su área sea máxima? Contenido Trigonometria Discriminante Propiedades de las raices Aplicaciones Función cuadratica Conocimiento I1 Concavidad Intersección eje Y Int. eje X Vértice Eje de simetría Gráfico Máximo y Mínimo II1a II1b II1c II1d II1e II1g Comprensión I4 II1f Aplicación I2,3 I5 I 6, 7 I14, II2a,b I8, 9, 11, 12, 16 I12 I10, 15 II3a,b,c,d 3 1 29 Total 3 1 3 5 6 0,5 0,5 3 1 1 1 6 31









