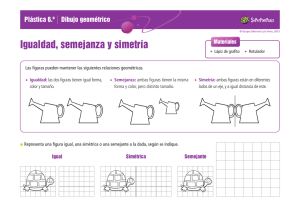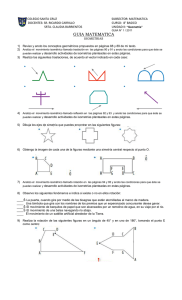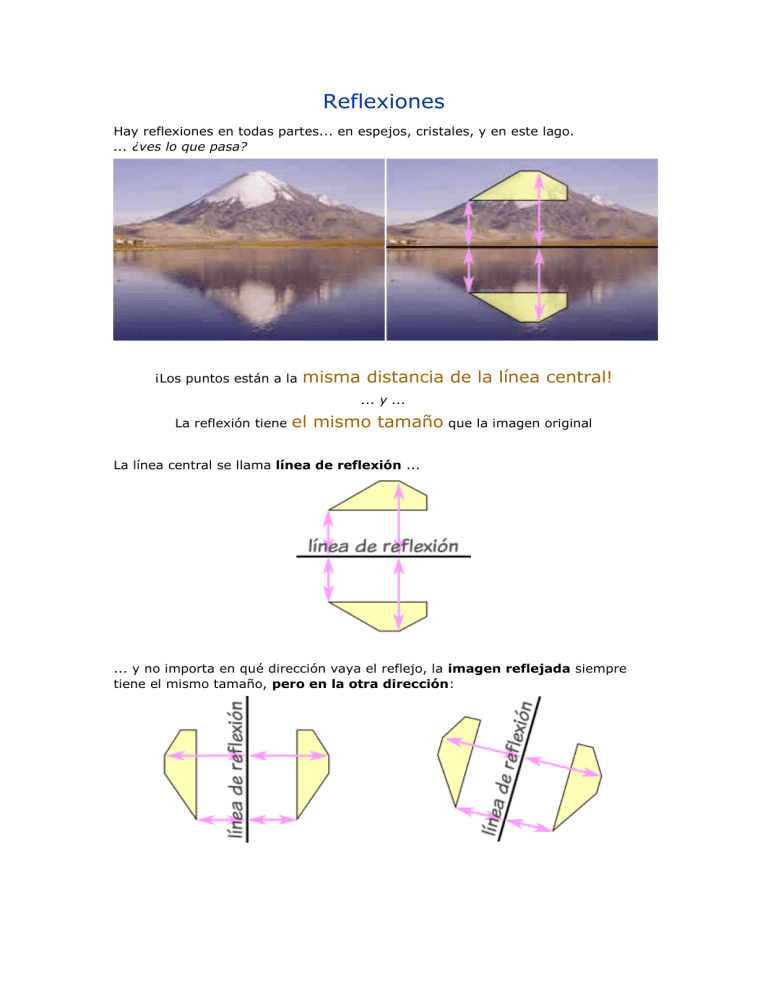
Reflexiones Hay reflexiones en todas partes... en espejos, cristales, y en este lago. ... ¿ves lo que pasa? ¡Los puntos están a la misma distancia de la línea central! ... y ... La reflexión tiene el mismo tamaño que la imagen original La línea central se llama línea de reflexión ... ... y no importa en qué dirección vaya el reflejo, la imagen reflejada siempre tiene el mismo tamaño, pero en la otra dirección: Una reflexión es un volteo con respecto a una línea Las transformaciones geométricas planas son operaciones que relacionan dos figuras geométricas en el plano a través de ciertas propiedades. Estas transformaciones también pueden entenderse como las relaciones geométricas, basadas en ciertas propiedades particulares cada una de ellas, que vinculan a dos figuras en el plano. La traslación es una transformación geométrica plana consistente en desplazar cada punto (y por tanto cada arista) de una figura según una dirección, sentido y distancia fijos. Estos tres datos conforman el denominado vector de la traslación. En una traslación, las figuras inicial y final guardan relación de igualdad. El producto de dos traslaciones es otra traslación, cuyo vector es la suma de los dos vectores de ambas traslaciones. La traslación suele usarse como paso final para situar figuras resultado de problemas geométricos que deben cumplir determinadas condiciones de posición. A continuación se detallan varios ejemplos. Ejemplo 1.- Dada una circunferencia de 2 cm de radio y una recta que está a 1 cm de su centro, encontrar un triángulo equilátero de lado 2,5 cm que tenga un lado sobre la recta y el vértice opuesto en la circunferencia. Dibujamos primero el triángulo apoyado en recta (primera condición) y luego aplicamos una traslación para que, sin dejarse de cumplir la primera condición, se cumpla la segunda (hay dos soluciones). Ejemplo 2.- Dibujar un cuadrado que tiene dos de sus vértices en dos paralelas dadas y otro en otra oblicua que las corta. Dibujamos el cuadrado con dos vértices en las rectas (primera condición) y después aplicamos una traslación para que, sin dejarse de cumplir la primera condición, se cumpla la segunda (hay dos soluciones). Ejemplo 3.- Dado un punto P y una recta r a 2 cm de distancia de él, dibujar una circunferencia de radio 2 cm que pase por el punto e intercepte a la recta en una cuerda de 3 cm. Dibujamos una circunferencia de radio 2 centrada en un punto cualquiera O1. Centrado en la perpendicular a la recta por O1 dibujamos el segmento de 3 cm, que proporciona los puntos A y B. Llevamos A sobre la circunferencia dando C. Aplicando la traslación inversa al vector AC obtenemos O2. Para colocarlo en su posición final, llevamos P sobre la circunferencia y aplicamos una nueva traslación, esta vez inversa al vector PD y obteniendo O3 (hay una segunda solución). La rotación es un movimiento que consiste en girar en un ángulo determinado todos los puntos de una figura en torno a un punto llamado centro de rotación. Por ejemplo: La figura muestra un remolino que se puede girar en torno a su centro cuando se soplan las aspas. Un giro de 90º en el sentido contrario al giro de las manecilla del reloj, produce que aspa señalada con un círculo quede en el lugar del aspa señalada con un rectángulo, ésta en el lugar de la que tiene un cuadrado, la que a su vez queda en el lugar de la señalada con un triángulo y esta última, en el lugar de la que tiene un círculo. Un giro de 360º produce que el aspecto del remolino no cambie al final del giro. Elementos necesarios que se deben tener claros para la definición Centro de rotación: Punto en torno al cual se rota o gira la figura (puede ser cualquier punto del plano, no necesariamente en la figura). Magnitud de giro: medida del ángulo en que se hace el giro. Este ángulo está formado por el centro de rotación, el segmento que une un punto cualquiera de la figura original con dicho centro y el segmento que une el punto correspondiente en la figura obtenida con el centro, después de la rotación. Sentido del giro: Este puede ser en contra o a favor del giro de las manecillas del reloj. En el primer caso se dice que el giro es positivo, en el caso contrario el giro es negativo. El sentido del giro se puede señalar mediante un signo + o - en el ángulo de rotación. Si no se especifica, se entiende que es positivo. Ejemplos de sentidos de giro Definición Una figura experimenta una rotación de centro O y magnitud de giro (positiva) si a cada punto P de la figura, se hace corresponder un punto P’ del plano, de modo que P y P` corresponden a un mismo arco de circunferencia de centro O y el ángulo POP’ mide . Ejemplo en el plano cartesiano: En la ilustración, el triángulo RPQ es la figura original que ha experimentado una rotación de centro O (el origen) y magnitud de modo que cada uno de sus puntos tiene su correspondiente en el triángulo R’P’Q’. Así R’ es el correspondiente de R; P’ y Q’ lo son de P y Q respectivamente. Podemos apreciar que la distancia entre O y P es la misma que entre O y P’ pues OP y OP’ son los radios de la misma circunferencia al estar P y P’ sobre el mismo arco, esto es equivalente para todos los puntos de las figuras. Reflexión, rotación y traslación geometrica Reflexión geométrica Una reflexión es una transformación geométrica. En una reflexión un objeto geométrico se mueve a través reto la cual se denomina recta de reflexión o eje de reflexión la figura reflejada siempre es una imagen de espejo de la figura original. Características de las reflexiones: Un objeto y su reflexión son simétricos sobre la recta de reflexión. Un objeto y su reflexión son congruentes. Un objeto y su reflexión son similares. Si un objeto reflejado es otra, vez de reflejado el objeto resultante es consiente con el objeto original. Rotación geométrica Es una transformación que consiste en realizar un giro a la figura respecto de un punto determinado y un ángulo de giro indicado. Cada punto de la figura se debe girar según el ángulo dado en sentido contrario a las manecillas del reloj (sentido anti horario),esto si el ángulo de giro da positivo. Características de rotación: Un punto denominado centro de rotación. Un ángulo. Un sentido de rotación. Cada punto sigue un circulo al rededor del centro. La distancia del centro a cualquier punto de la figura es la misma. Traslación geometría Una traslación geométrica es una transformación mediante la cual se realiza un cambio de posición de la figura en el plano. Este cambio de lugar esta dado por un vector. Las traslaciones están dadas por tres elementos: 1. La dirección;si es horizontal, vertical u oblicua. 2. El sentido; derecha, izquierda, arriba o abajo. 3. Y la magnitud de desplazamiento que se refiere a cuantas unidades de longitud se desplaza la figura. PROPIEDADES DE LAS ROTACIONES, REFLEXIONES Y TRASLACIONES Autor: Isamar Promotor INTRODUCCIÓN En nuestra vida cotidiana, al igual que en la naturaleza, nos encontramos con multitud de situaciones en las que está presente la simetría... si nos fijamos en nuestro cara veremos que ojos, nariz, orejas, boca son simétricas respecto a un eje imaginario. El cuerpo de las mariposas es uno de los más bellos ejemplos de simetría en la naturaleza, así como los paisajes que se reflejan en la superficie del agua de lagos. La lista de objetos y seres vivos que tienen forma simétrica sería interminable.En un dibujo o una imagen impresos podemos comprobar si la figura representada es simétrica si al doblar por un eje hacemos que coincidan todos los puntos. Ocurre lo mismo al recortar un papel doblado. OBJETIVO Clasificar y caracterizar la traslación, la simetría y la rotación de figuras en un plano. Transformar figuras, aplicando: traslaciones, reflexiones y rotaciones. Describir los cambios que se observan entre una figura y su imagen por traslación rotación y simetría Describir patrones que se observan en la aplicación de traslaciones, reflexiones y rotaciones en el plano cartesiano Reconocer simetrías, rotaciones y traslaciones en la naturaleza, en la ciencia, en diseños estructurales y tecnológicos y en obras de arte, (de Escher, entre otros), algunas artesanías. EXPLORA SIMETRÍA AXIALLa simetría axial (también llamada rotacional, radial o cilíndrica) es la simetríaalrededor de un eje, de modo que un sistema tiene simetría axial o axisimetríacuando todos los semiplanos tomados a partir de cierto eje y conteniéndolo presentan idénticas características. La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo. SIMETRÍA AXIAL DE UN TRIANGULO SIMETRÍA CENTRAL La simetría central, en geometría, es una transformación en la que a cada punto se le asocia otro punto llamado imagen, que debe cumplir las siguientes condiciones:a) El punto y su imagen están a igual distancia de un punto llamado centro de simetría.b) El punto, su imagen y el centro de simetría pertenecen a una misma recta. SIMETRÍA CENTRAL DEL PUNTO A SIMETRÍA CENTRAL DEL TRIANGULO ABC, RESPECTO DEL PUNTO 0 Conocimiento previo Traslación: es el movimiento directo de una figura en la que todos sus puntos: Se mueven en la misma dirección. Se mueven la misma distancia. El resultado de una traslación es otra figura idéntica que se ha desplazado una distancia en una dirección determinada. Cuando movemos un mueble en una misma dirección lo estamos trasladando. El tren se traslada a lo largo de una vía recta. El ascensor nos traslada de una planta a otra... Estas y muchas otras más son situaciones en las que el movimiento de traslación está presente en nuestras vidas. Rotación o giro: es un movimiento alrededor de un punto que mantiene la forma y el tamaño de la figura original. Una rotación se determina por estos tres elementos: Un ángulo que determina la amplitud de la rotación. Un punto llamado centro de rotación. Un sentido de la rotación que puede ser del mismo sentido de las agujas del reloj o en sentido contrario. La vida cotidiana está llena de situaciones en las que la rotación o giro está presente. Cuando abrimos o cerramos una puerta estamos haciendo una rotación sobre un punto o centro de rotación, las ruedas de nuestra bicicleta giran sobre el eje central, al igual que los pedales, giramos al montar en los caballitos, al abrir y cerrar el abanico hacemos que gire sobre un punto, al mover la ruleta hacemos que gire igualmente sobre su centro. Simetría: La simetría respecto a un eje es una reflexión. Los cuerpos se reflejan en el agua, en una superficie pulida, en los espejos. El objeto que vemos reflejado decimos que es su simétrico. Este tipo de simetría, con respecto a un eje, se caracteriza porque: Los puntos simétricos de una figura y los de la figura reflejada están sobre la misma línea. Los puntos de ambas figuras están a la misma distancia del eje de simetría en direcciones opuestas. La figura reflejada siempre tiene el mismo tamaño, pero en la dirección opuesta. En nuestra vida cotidiana, al igual que en la naturaleza, nos encontramos con multitud de situaciones en las que está presente la simetría... si nos fijamos en nuestro cara veremos que ojos, nariz, orejas, boca son simétricas respecto a un eje imaginario. El cuerpo de las mariposas es uno de los más bellos ejemplos de simetría en la naturaleza, así como los paisajes que se reflejan en la superficie del agua de lagos. La lista de objetos y seres vivos que tienen forma simétrica sería interminable. En un dibujo o una imagen impresos podemos comprobar si la figura representada es simétrica si al doblar por un eje hacemos que coincidan todos los puntos. Ocurre lo mismo al recortar un papel doblado. PROPIEDADES Simetría axial En la simetría axial, una línea recta puede dividir las figuras u objetos en dos figuras congruentes. Si las partes se colocan una encima de otra y no coinciden, entonces se trata de una congruencia inversa, es decir, coinciden por superposición si se les hace girar en torno al eje. Al trazar figuras simétricas respecto a un eje, el trazo se hace tantas veces como puntos (vértices) tenga cada figura. PROPIEDADES Simetría central · Cuando se realizan dos movimientos continuos de simetría axial con ejes perpendiculares, resulta que la segunda imagen tiene simetría central con respecto a la figura original. · El centro de simetría es el punto donde se cortan los dos ejes. · Si se desea obtener una figura simétrica con respecto a otra y en relación con un centro de simetría, el proceso para obtener una figura congruente se repite tantas veces como vértices tenga el polígono que se quiere reflejar. · Los triángulos presentan congruencia, pues sus ángulos se pueden hacer coincidir entre sí. simetría axial es toda aquella simetría que se produce alrededor de un eje. Es decir, aquella que tiene lugar cuando los semiplanos que se toman a partir de un mencionado eje, al que contienen, presentan idénticas características. En la simetría axial se produce el mismo fenómeno que se da al reflejar cualquier objeto en un espejo. A los puntos que pertenecen a la figura simétrica se les llama puntos homólogos, es decir, A’ es homólogo de A, B’ es homólogo de B, y C’ es homólogo de C. Además, las distancias existentes entre los puntos de la figura original son iguales que las distancias entre los puntos de la figura simétrica. Esta pagina es muy útil para ampliar el conocimiento sobre simetría axial de una manera fácil y entretenida, se puede utilizar en alguna clase para que los alumnos comprendan mas sobre dicho tema. http://recursostic.educacion.es/gauss/web/materiales_didacticos/primaria/actividades/geom etria/simetrias/simetria_axial/actividad.html La simetría central, en geometría, es una transformación en la que a cada punto se le asocia otro punto llamado imagen, que debe cumplir las siguientes condiciones: REPORT THIS AD a) El punto y su imagen están a igual distancia de un punto llamado centro de simetría. b) El punto, su imagen y el centro de simetría pertenecen a una misma recta.