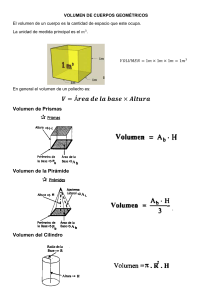
SSSUPERFICIES POLIEDRICAS POLIEDROS CON GRAFICOS, ELEMENTOS DE LOS PILIEDROS, CLASIFICACION DE PILIEDROS, CLASES DE POLIEDROS SEGÚN EL NUMERO DE CARAS CAMILA MOGOLLON DEIMER HENRIQUEZ 7-04 LIC. GAWER DORIA GEOMETRÍA INSTITUCION EDUCATIVA JUAN XXlll PURSIMA CORDOBA JULIO 2019 SUPERFICIES POLIÉDRICAS, RADIADAS Y ESFERERAS Características Las superficies poliédricas están limitadas por polígonos, que se cortan dos a dos en rectas llamadas aristas que, tres o más bordes coinciden en puntos llamados vértices. Pueden ser o no regulares. Los poliedros regulares son el tetraedro, el cubo, el octaedro, el dodecaedro, el icosaedro. Las superficies radiadas están limitadas por rectas que confluyen en un vértice que puede estar en el infinito: como el cono, el cilindro, la pirámide y el prisma. La esfera es el lugar geométrico de los puntos del espacio que equidistan de un punto fijo llamado centro de la esfera. En la figura vemos un dodecaedro apoyado en una arista, representado en caballera Poliedros Un poliedro es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego clásico, de la raíz «muchas», «base», «asiento», «cara». Los poliedros se conciben como cuerpos tridimensionales, pero hay semejantes topológicos del concepto en cualquier dimensión. Así, el punto o vértice es el semejante topológico del poliedro en cero dimensiones, una arista o segmento lo es en 1 dimensión, el polígono para 2 dimensiones; y el polícoro el de cuatro dimensiones. Todas estas formas son conocidas como poli topos, por lo que podemos definir un poliedro Elementos de los poliedros En un poliedro podemos distinguir los siguientes elementos: Caras: son los polígonos que forman el poliedro Aristas: son los segmentos donde hacen intersección las caras. Vértices: son los puntos donde hacen intersección las aristas. Ángulo diedro es el ángulo que forman dos caras que se cortan. Hay tantos como número de aristas. Ángulo poliedro, determinados por las caras que inciden en un mismo vértice. Hay tantos como número de vértices. CLASIFICACION DE POLIEDROS Solo existen 5: tetraedro, hexaedro o cubo, octaedro, dodecaedro e icosaedro, regulares. · Poliedros no regulares: no tienen todas sus caras, aristas o ángulos iguales. Hay infinitos poliedros irregulares, por lo que, este gran grupo, se divide en familias, con numerosos poliedros (infinitos en muchos casos) CLASES DE POLIEDROS SEGÚN EL NUMERO DE CARAS Existen varios tipos de poliedro. Los poliedros se pueden clasificar mediante dos criterios: Según su regularidad: Regulares: un poliedro regular es aquel que sus caras son poliedros regulares y son todos iguales. Todos los ángulos poliedros también son iguales. Irregulares: Poliedro cuyas caras son polígonos no todos iguales. Según si son poliedros convexos o cóncavos: Poliedro convexo: si todo par de puntos de la superficie del poliedro puede ser unido por una línea recta que no sale en ningún momento del interior del poliedro Poliedro cóncavo: si existe al menos un par de puntos de la superficie de la figura que para unirlos mediante una línea recta, necesariamente dicha recta tiene que salir del interior del poliedro Poliedro convexo: si todo par de puntos de la superficie del poliedro puede se Tetraedro: poliedro irregular con cuatro caras Pentaedro: poliedro irregular con cinco caras Hexaedro: poliedro irregular con seis caras Heptaedro: poliedro irregular con siete caras Octaedro: poliedro irregular con ocho caras Eneaedro: poliedro irregular con nueve caras Decaedro: poliedro irregular con diez caras