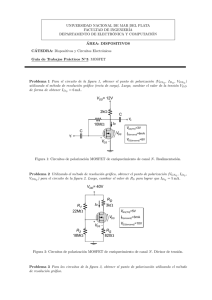
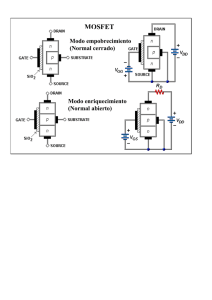
POLARIZACION DEL TRANSISTOR DE EFECTO DE CAMPO DE UNION J-FET (JUNTION FIELD EFFECT TRANSISTOR) TEORIA PREVIA El transistor de efecto de campo (JFET) tiene las siguientes ventajas y desventajas con respecto del transistor bipolar VENTAJAS - su impedancia de entrada es extremadamente alta (típicamente 100M Ω o más). - Su tamaño físico es aproximadamente un 20 o 30% del espacio que ocupa un BJT. Esto lo hace idóneo para su integración en gran escala, sobre el MOSFET que es más pequeño que el JFET. - Su consumo de potencia es mucho más pequeña que la del BJT. - Su velocidad de conmutación es mucho mayor que la del BJT. - Es menos ruidoso que el BJT, esto lo hace idóneo para amplificadores de alta fidelidad. - Es afectado en menor grado por la temperatura. DESVENTAJAS - Su ganancia de voltaje es mucho menor que en el BJT. Es susceptible al daño en su manejo, sobre todo el MOSFET. Su ancho de banda o respuesta en frecuencia es menor que en el BJT. CONSTRUCCIÓN FUNCIONAMIENTO 1.- VGS = 0 y VDS variable El canal n se comporta como una resistencia cuyo valor depende del voltaje existente entre D y S. Cuando VDS llega a ser lo suficientemente grande la corriente iDS comienza a ser constante, VDS puede incrementarse hasta BVDS0 (punto en el que ocurre el rompimiento por avalancha), la nomenclatura significa “voltaje de ruptura entre D y S con VGS = 0”. La curva que se obtiene para cuando se mantiene en corto las terminales de Gate y Source, mientras varia el voltaje entre Dren y Source, es la siguiente: IDSS = Corriente entre D y S con VGS = 0. VPO = Voltaje entre D y S a partir del cual la corriente comienza a ser constante. Aquí comienza la región de saturación BVDS0 = Voltaje de ruptura entre D y S con VGS = 0. NOTA: Como el canal N se comporta como una resistencia a medida que se incrementa VDS, entonces el mismo potencial presente en el canal hace que se forme una región de agotamiento o campo eléctrico que va incrementándose en intensidad hasta que se cierra por completo en el punto A, cualquier aumento posterior en la tensión VDS mantendrá al potencial de A con respecto de tierra constante, razón por la cual la corriente i DS comienza a ser constante. 2.- VGS y VDS variables: El voltaje VGS es negativo en los FET`S de canal N, esto para controlar la anchura del canal, a medida que se incrementa VGS negativamente se origina una región de agotamiento entre compuerta y fuente que va reduciendo la corriente iDS gradualmente: Denotaremos por VPX a un voltaje cualquiera producido bajo la condición de un voltaje VGS de valor “x” y en el cual la corriente comienza a hacerse constante (saturarse). La relación existente entre el nuevo VPX y cualquier VGS es: VPX = Vpo + VGS BVDSX = BVDS0 + VGS El canal se cierra por completo cuando VGS = VGsoff, en este momento la corriente iDS es aproximadamente cero. CURVA DE TRANSCONDUCTANCIA Es una grafica de la corriente de salida en función del voltaje de entrada. La ecuación que representa a esta curva es: iDS v = I D SS 1 − GS VGSoff 2 ÷ ÷ 2 iDS ó iDS = IPO v = I PO 1 + GS ÷ VPO donde IDSS = IPO y VGSoff = -Vpo Algunos parámetros importantes del FET son los siguientes: IDSS = Corriente de saturación entre D y S con la tensión VGS = 0. VGSoff = Voltaje que produce la oclusión o cierre del canal. IGSS = Corriente inversa de saturación entre G y S con VDS = 0. BVDS0 = voltaje de ruptura entre D y S con VGS = 0. BVGSS = Voltaje de ruptura entre G y S con VDS = 0. YfS = Admitancia de transferencia directa para source común con VGS = 0. EJERCICIO: El JFET 2N5457 tiene los siguientes parámetros: IDSS = 5mA VGSoff = -6V IGSS = 1nA BVGSS = -25V YFS = gFS = 5000 µS 1.- Obtener la ecuación de la curva de transconductancia. 2 iDS v = 5mA 1 − GS ÷ −6 iDS v = 5mA 1 + GS ÷ 6 2 2.- Obtener la corriente entre drenador y fuente para los siguientes voltajes compuertafuente. VGS iDS 0V 5mA -2 2.22mA -4 .555mA -6 0 -8 .555mA El resultado iDS = .555mA para VGS = -8 no existe ya que para el funcionamiento del FET es solo media parábola. 3.- Calcular la impedancia de entrada de este dispositivo cuando VGS = -15V a temperatura ambiente y a 100º C. Z i 25o C = VGS −15V = I GSS 1nA Zi = 15GΩ I GSS 100 C = Zi ( 25o C ) =2 T2-T1 10 I GSS 100 C = 181.02nA Zi (100o C ) = −15V 181nA Zi (100o C ) = 83M Ω TRANSCONDUCTANCIA EN UN PUNTO Si derivamos la ecuación de la curva de transconductancia se obtendrá el valor de la conductancia en un punto en particular sobre la curva llamado gm: V ∂I DSS 1 − GS VGSoff = ∂VGS gm = ∂iDS ∂VGS gm = 2 I DSS −VGSoff V 1 − GS VGSoff 2 ÷ ÷ ÷ ÷ gm indica que tanto control tiene el voltaje de entrada VGS sobre la corriente de salida: En la figura se observa como para un mismo incremento de VGS se obtienen diferentes amplitudes de corriente. Q2 tiene mayor pendiente, es decir mayor conductancia, por lo tanto hay un mayor control de iDS para el mismo VGS. POLARIZACIÓN DEL JFET Algunas de las formas típicas de polarización de un JFET son las siguientes: - POLARIZACIÓN FIJA O DE COMPUERTA AUTOPOLARIZACIÓN POLARIZACION POR DIVISIÓN DE VOLTAJE POLARIZACION POR FUENTE DE CORRIENTE POLARIZACIÓN FIJA Al igual que en el BJT, la malla de entrada es la que polariza al JFET, en este caso la malla de compuerta. Cabe mencionar que para este dispositivo la corriente de reposo es fijada por el voltaje de compuerta. ANALISIS El voltaje en la compuerta siempre será negativo respcto al Terminal de Source en jun JFET de canal N: VGS = VG (+) – VS (-) ANÁLISIS EN LA MALLA DE COMPUERTA Ley de Voltajes de Kirchoff en malla de compuerta. +VGG + VRG + VGS = 0 Como se supone que la unión compuerta-fuente esta polarizada inversamente, entonces significa que no existe corriente y por lo tanto VRG = 0 VGS = -VGG Esta ecuación representa la recta de polarización Esta recta se muestra en la siguiente figura, la cual queda representada por una recta vertical a lado izquierdo del eje de la corriente. De la figura se observa la gran inestabilidad que puede experimentar el punto de operación para el caso de los posibles cambios en los parámetros que puede presentar un FET aún cuando tratándose del mismo tipo ya que las técnicas de fabricación no son tan perfectas como para que IDSS y VGS off sean constantes de un dispositivo a otro. Este tipo de polarización es la peor forma de polarizar a un JFET ya que el punto de operación (IDSQ, VDSQ) bastante es inestable. ANÁLISIS EN LA MALLA DEL DREN Por Ley de Voltajes de Kirchoff -VDD + VRD + VDS = 0 En terminus de la corriente de Dren: VDD = IDSRD + VDS iDS = VDD −VDS RD Ecuación de la recta de carga en C.C. En la figura, el punto de operación depende el punto de operación fijado en la curva de transconductancia. EJEMPLO: Encontrar la variación del punto de operación para el circuito mostrado: VDD = 12V VGG = -1V RD = 470Ω RG = 1MΩ FET 2N5486 I DSSMAX = 20mA I DSSMIN = 8mA V = −6V GSoff max VGSoff min = −2V SOLUCIÓN 2 IDSQmax = 20mA 1 − IDSQmin = 8mA 1 − −1 = 13.89mA −6 2 −1 = 2mA −2 ∆IDSQ = 11.9mA AUTOPOLARIZACIÓN LVK en malla de compuerta VRG +VGS +VRS = 0 VGS + RS iDS = 0 i DS = − VGS RS A esta ecuación se le conoce como ecuación de la recta de polarización. Esta recta tiene pendiente negativa y pasa por el origen, como se observa en la siguiente figura: La recta representa una RS pequeña y proporciona un elevado valor de g m , ideal para una buena ganancia de corriente, la desventaja es la inestabilidad debido a los cambios en los parámetros del JFEt, como puede observarse. La recta ofrece las mejores condiciones tales que no compromete la inestabilidad y los valores de transconductancia, es decir, no se sacrifican una u otra. La recta produce buena estabilidad del punto de operación, sin embargo produce valores de g m bajos que se traducen en una baja ganancia de corriente. Generalmente muchos diseñadores optan por el tipo de polarización dado por la recta Este tipo de polarización es mejor que la polarización fija ya que el punto de operación es más estable. En la recta la RS puede llamarse óptima ya que esta recta pasa por el centro de una de las curvas de transconductancia. RS óptima puede calcularse: RS = VGSoff I DSS Las coordenadas del punto de operación cuando se presenta RS óptima es: I DSQ = 0.382 I DSS VGSQ = 0.382 VGSoff Estas ecuaciones pueden demostrarse a partir del siguiente análisis: i DS 2 V = I DSS 1 − GS V GSoff Normalizando: i DS V = 1 − GS I DSS VGSoff 2 Si el punto de operación esta a la mitad de la curva entonces: i DS VGS = =K I DSS VGSoff ∴ K = (1 − K ) 2 K = 1 − 2K + K 2 K 2 − 3K + 1 = 0 Resolviendo la ecuación cuadrática: K1 = −0.382 K 2 = 2.48 Como: K= iDS ó I DSS i DS = K1 I DSS Y como i DS < I DSS entonces la solución es: K1 = 0.382 . El mismo razonamiento se obtiene para VGSQ VGSQ = 0.382VGSoff ANÁLISIS EN LA MALLA DE DREN LVK en malla de compuerta −VDDVRD + vDS + VRS = 0 VDD = iDS ( RD + RS ) + vDS iDS = VDD − vDS RD + RS A esta ecuación se le conoce como ecuación de la recta de carga en C.C. EJERCICIO: Polarizar el FET de la figura de tal modo que el punto de operación se ubique a la mitad de la curva de transconductancia y a la mitad de la recta de polarización. Calcular además el valor de g m en el punto de operación. Solución: RS = VGSoff I DSS RS = 214Ω ≈ 220Ω RD = VRD I DSQ La coordenada del punto Q cuando se elige Rs óptima es: I DSQ = 0.382 I DSS = 5.35mA VGSQ = −1.15V ∴RD = RD = V −VDSQ −VRS VRD = DD I DSQ I DSQ 12 − 6 − 220( 5.35mA) 5.35mA RD = 900Ω RG se propone de un valor de tal modo que se aproveche la alta impedancia del JFET. En este caso se propone de: RG = 1MΩ 1 − VGS VGSoff 2(14 mA) − 1. 5 = 1 − − ( − 3) −3 gm = gm 2 I DSS −VGSoff g m = 5768µS POLARIZACIÓN POR DIVISOR DE VOLTAJE Para simplificar el análisis en la malla de compuerta encontraremos el circuito equivalente de Thévenin para facilitar. LVK en malla de compuerta: −V + VRG + vGS + VRS = 0 VGG = vGS + RS iDS iDS = VGG − vGS RS Esta ecuación representa la ecuación de la recta de polarización. Esta ecuación puede escribirse como: V 1 iDS = − VGS + GG RS RS Es una recta con pendiente negativa y con la ordenada en el origen a observa en la figura: VGG como se RS De la figura puede observarse que este tipo de polarización es mejor que las dos anteriores debido a que ∆ I DSQ es menor, sin embargo para conseguir esto es necesario aplicar valores elevados de VDD para que VGG sea lo más grande posible y asi el punto de operación sea más estable. ANÁLISIS EN LA MALLA DE DREN VDD = VRD + VDS + VRS VDD = i DS ( RD + RS ) + VDS i DS = VDD − VDS RS + RD Esta es la Ecuación de la recta de carga EJERCICIO: Polarizar un JFET por divisor de tensión y de tal modo que se cumplan los siguientes datos: Punto de operación a la mitad de la recta de carga y a la mitad de la curva de transconductancia, el voltaje de alimentación VDD = 12V y calcular el valor de g m en el punto de operación. Solución: Se elige arbitrariamente VGG = 2 V I DSQ = 0.382 I DSS = 3.06mA VGSQ = 0.382VGSoff = −1.91V I DSQ = Rs = VGG −VGSQ VGG Rs −VGSQ I DSQ = 3.91V 3.06mA Rs = 1278Ω RD = VDD −VDSQ −VRS I DSQ = 12 − 6 − 3.91V 3.06mA RD = 683Ω R1 = RG V R = 1MΩ 1 − GG Eligiendo G VDD R1 = 1.2 MΩ R2 = VDD RG VGG R2 = 6 M Ω EJERCICIO: Para cada uno de los circuitos de polarización con FET, determinar el punto de operación. a) Solución: El punto de operación se obtiene analíticamente a partir de la intersección de la curva de transconductancia con la recta de polarización. i DS i DS V = I DSS 1 − GS VGSoff V −VGS = GG Rs 2 igualando ambas ecuaciones obtenemos el punto de operación. VGG −VGSQ Rs VGG − VGSQ RsI DSS 1 VGSoff 2 =1− V = I DSS 1 − GSQ VGSoff 2VGSQ VGSoff + VGSQ 2 VGSoff 2 1 2 2 VGSQ + − RsI VGSoff DSS VGSQ + 1 = 0 Esta ecuación tiene analogía con: ax 2 + bx + c donde 1 1 a= = = 0.0625 2 16 VGSoff b= 1 2 − = 0.604 RsI DSS VGSoff c =1 x = VGSQ Resolviendo la ecuación cuadratica: 2 VGSQ = − 0.604 ± ( − 0.604 ) 2 − 4( 0.0625) 2( 0.0625) VGSQ1 = −7.546V VGSQ 2 = −2.12V Este último valor de VGSQ es el correcto ya que para el otro, el canal estaría cerrado por completo e I DSQ = 0 . I DSQ = − VGSQ VRS = Rs Rs I DSQ =1.767mA o de otra manera 2 − 212 I DSQ = 8mA1 − −4 I DSQ =1.767mA gm = 2 I DSS − VGSoff V 1 − GSQ VGSoff g m = 1880 µS VDSQ = VDD − I DSQ ( RD + Rs ) VDSQ = 4.05V b) DATOS VDD = 12V I DSS = 6mA VGS OFF = −3V rds = 25K Ω R1 = 100 K Ω R2 = 1M Ω RS = 1K Ω RD = 1.6 K Ω rs = 50Ω RL = 1.2 K Ω La curva de transconductancia es: i DS V = I DSS 1 − GS V GSoff 2 La recta de polarización es: V − VGS i DS = GG Rs igualando ambas ecuaciones para encontrar el punto de operación: VGG −VGSQ Rs VGG −VGSQ I DSS Rs V = I DSS 1 − GSQ VGSoff =1 − 2VGSQ VGSoff + 2 VGSQ 2 VGSoff 2 Reacomodando: 1 V GSoff 2 V GSQ 1 2 + − RsI V GSoff DSS 2 V GG V GSQ + 1 − =0 I DSS R S ax 2 + bx + c 1 1 a = = 2 9 V GSoff b= 1 2 − = 0.833 RsI DSS VGSoff c =1− VGG = VGG I DSS Rs R1 VDD R1 + R2 VGG = 1.091 c = 0.818 − 0.833 ± VGSQ = ( − 0.833) 2 − 4 1 ( 0.818) 9 1 2 9 VGSQ1 = −6.338V VGSQ 2 = −1.16V I DSQ = I DSQ VGG − VGSQ Rs 1.091 − ( − 1.16 ) = 1000 I DSQ = 2.25mA VDSQ = VDD − I DSQ ( RD + Rs ) VDSQ = 6.15V gm = 2 I DSS VGSoff V 1 − GSQ VGSoff g m = 2451µS