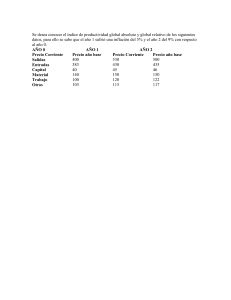
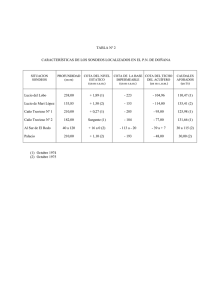
Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata Introducción al análisis numérico PRESENTACION Al momento de aplicar las Matemáticas a situaciones del mundo real nos encontramos a menudo con problemas que no pueden ser resueltos analíticamente o de manera exacta y cuya solución debe ser abordada con ayuda de algún procedimiento numérico. ¿Qué es un método numérico? Un método numérico es un procedimiento mediante el cual se obtiene, casi siempre de manera aproximada, la solución de ciertos problemas realizando cálculos puramente aritméticos y lógicos (operaciones aritméticas elementales, cálculo de funciones, consulta de una tabla de valores, cálculo preposicional, etc.). Tal procedimiento consiste de una lista finita de instrucciones precisas que especifican una secuencia de operaciones algebraicas y lógicas (algoritmo), que producen o bien una aproximación de la solución del problema (solución numérica) o bien un mensaje. La eficiencia en el cálculo de dicha aproximación depende, en parte, de la facilidad de implementación del algoritmo y de las características especiales y limitaciones de los instrumentos de cálculo (las computadoras). En general, al emplear estos instrumentos de cálculo se introducen distintos tipos de errores. Teoría de Errores Clasificación de los errores Errores sistemáticos Estos se deben a los instrumentos de medida ya que estos están sometidos a influencias externas: cambios en la temperatura, la humedad, los defectos de fabricación, la impericia del experimentador… Estos errores no pueden eliminarse totalmente y para que su incidencia sea la mínima, se realizan pruebas de control que consisten en cotejar medidas de un objeto patrón con diferentes instrumentos. Errores Inherentes En la formulación de problemas aplicamos un modelo matemático que resulta ser una aproximación a la realidad, esto induce errores. Este tipo de errores se llaman errores inherentes. Errores por redondeo En los cálculos se presentan números que intervienen en los mismos mediante su expresión decimal; ofrece ésta la ventaja de la uniformidad del cálculo, pero también el inconveniente de exigir infinitas cifras (tanto para los números irracionales como para los racionales). Debemos, entonces, prescindir de estas infinitas cifras desde una de ellas en adelante, en virtud de lo cual los resultados no serán exactos; esta limitación en el numero de cifras se denomina redondeo. Dado el número exacto: α = 0, a1 a2… ar ar+1 ar+2…x 10k (con a1≠ 0) Apunte creado por el Ing. Amiconi Diego Federico - 1 - Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata las formas de redondeo son: a) Redondeo por defecto con r cifras: Consiste en tomar como valor aproximado de α a: a = 0, a1 a2…ar x 10k b) Redondeo por exceso con r cifras: Se toma como valor aproximado de α a: ā = 0, a1 a2…ar + 1 x 10k c) Redondeo al valor mas próximo con r cifras: Veo que ocurre con la cifra “r+1”. Consiste en adoptar como valor aproximado de α, respectivamente a: c1) defecto) si ar+1 < 5 c2) si exceso) ar+1 > 5 a = 0, a1 a2…ar x 10k (por ā = 0, a1 a2…ar + 1 x 10k (por Errores de truncamiento (es el redondeo por defecto) Estos errores se presentan cuando los procedimientos de cálculos involucran un número arbitrariamente grande de operaciones. En tal caso debemos interrumpir el proceso luego de un número finito de ellas; los términos omitidos introducen un error en los resultados, denominado error de truncamiento. Ej.: Esto sucede cuando se aproxima el valor de una función en un punto mediante la suma de los n primeros términos de un desarrollo en serie de potencia para la función. Consideraciones sobre los errores En un proceso infinito de cálculo (por ejemplo en el caso de desarrollo en series), una forma de disminuir el error por truncamiento es aumentar el número de términos involucrados en el cálculo, pero con esto aumenta el número de operaciones, con lo cual el error por redondeo crece. Como el error total cometido será la suma de ambos, debemos procurar que sea éste último el que tome valores mínimos. Cifras significativas Todo número positivo α puede expresarse como la suma de productos de cada uno de sus dígitos multiplicado por una potencia de 10. α = am · 10m + am-1 · 10m-1 + …. + am-n+1 · 10m-n+1 + … Donde am ≠ 0 am, am-1,…= Dígitos del numero dado. m = Entero, potencia mas elevada de 10. Ejemplo Apunte creado por el Ing. Amiconi Diego Federico - 2 - Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata 718,45 = 7 · 102 + 1 · 101 + 8 · 100 + 4 ·10-1 + 5 ·10-2 En los cálculos se trabajamos con un número aproximado a, que tiene un número finito de cifras: a = am · 10m + am-1 · 10m-1 + …. + am-n+1 · 10m-n+1 Los ai (i = m, m-1,…) se llaman cifras significativas del numero aproximado a. Problemas fundamentales de cálculo con números aproximados Cuando se opera con números aproximados se presentan dos cuestiones de importancia: a) Determinar los errores en los resultados finales y parciales de los cálculos. b) Determinar el grado de aproximación que debe exigirse a los datos para obtener resultados con una aproximación prefijada. Errores Absoluto, relativo y porcentual Error Absoluto: Es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida. El error absoluto de una medida no nos informa por sí solo de la bondad de la misma. Es evidente, que no es igual de grave tener un error absoluto de 1 cm al medir la longitud de una carretera que al medir la longitud de un folio. Si α es un número exacto y a un valor aproximado de α, se llama error absoluto asociado con a al valor: ∆(a) = α – a Ejemplo: Cuando decimos que la longitud de una mesa es de 90,5 cm es posible que podemos afirmar que: a) dicha longitud está comprendida entre 90 y 91 cm o que afinando más la medición, b) afirmemos que está comprendida entre 90,4 y 90,6 cm. De ser cierta la primera hipótesis, el error absoluto sería menor o igual a 0,5 cm; mientras que de ser cierta la segunda, dicho error sería menor o igual que 0,1 cm. 90 < valor medida < 91 90,4 < valor medida < 90,6 - ea < 0,5 cm ea < 0,1 cm En el primer caso la cota del error absoluto es 0,5 cm y en el segundo caso 0,1 cm. La segunda medida es más precisa que la primera. Apunte creado por el Ing. Amiconi Diego Federico - 3 - Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata Error Relativo: Es el cociente (la división) entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto por ciento (%) de error (error Porcentual). Al igual que el error absoluto, puede ser positivo o negativo (según lo sea el error absoluto) porque puede ser por exceso o por defecto. El error Relativo no tiene unidades. Ej: En la medida de 1 m se ha cometido un error de 1 mm, y en 300 Km, 300 m. ¿Qué error relativo es mayor?. Respuesta: son iguales Se denomina error relativo ε(a), asociado con el valor aproximado a de un número exacto α al cociente entre el error absoluto y el valor exacto. ε(a) = ∆(a) α (con α ≠0) Los errores absolutos y relativos son en general imposibles de calcular, pues se desconoce frecuentemente el valor exacto. Para el error relativo tomaremos: ε(a) = ∆(a) a Cota superior del error absoluto Se llama cota superior del error absoluto del número aproximado a, a todo número real * positivo ∆ (a) que verifique: │ α – a │ = │∆(a)│< ∆*(a) De aquí resulta para el número exacto α: a – ∆*(a) < α < a + ∆*(a) Por brevedad suele escribirse para los valores limites: α = a ± ∆*(a) Cota superior del error relativo Se llama cota superior del error relativo del número aproximado a, a todo número real * positivo ε (a) que verifique: │ ε(a) │ < ε*(a) De la definición de error relativo: │ ε(a) │ = │∆(a)│ │a│ Apunte creado por el Ing. Amiconi Diego Federico - 4 - Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata * Teniendo en cuenta que │∆(a)│< ∆ (a) podemos decir que: │ ε(a) │ < ∆*(a) │a│ En consecuencia podemos adoptar como una cota superior de ε(a): ε*(a) = ∆*(a) │a│ Error porcentual Se llama error porcentual δ(a) del número aproximado a, a: δ(a) = 100 x ε(a) Análogamente a los casos anteriores llamamos cota superior de δ(a) a todo número real positivo que verifique: │δ(a) │ < δ*(a) Se cumple: δ*(a) = 100 x ε*(a) Cifras Exactas de un número aproximado Un número aproximado a se lo expresa de la forma: a = 0, a1 a2 …am x 10k (con a1 ≠ 0) -Diremos que tiene todas sus cifras exactas si se verifica: │∆(a) │ = │ α – a │ < 10-m · 10k El error absoluto se conserva en valor absoluto, inferior a una unidad del orden de la última cifra. - Diremos que un número aproximado: a = 0, a1 a2 …am x 10k Tiene todas sus cifras exactas (en sentido estricto) si se verifica: │∆(a) │ ≤ (1/2) 10-m · 10k El error no supera, en valor absoluto, media unidad del orden de la última cifra. Apunte creado por el Ing. Amiconi Diego Federico - 5 - Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata Aclaración: Algunos autores llaman cifras significativas a lo que aquí hemos denominado cifras exactas. Ejemplos: 2,003 tiene cuatro cifras significativas 0,0020 tiene dos cifras significativas (el 2 y el 0 de la derecha) 22,0 tiene tres cifras significativas. Formula general para el cálculo de errores en funciones Problema directo e inverso de errores. La determinación del error de un valor obtenido como resultado de operaciones sobre cantidades cuyos errores se conocen, constituye el método directo del cálculo de errores. Por otra parte, la estimación de los errores de los valores que intervienen en una cantidad de manera de que ésta sea calculada con un error prefijado, constituye el método inverso del cálculo de errores. La solución de estos problemas se apoyan en las fórmulas de propagación de errores. Método Directo Dados los errores asociados a las variables x1, x2….,xn; se trata de determinar el error del valor numérico de una cierta función asociada a las variables x1,x2…xn. Entonces la función u esta dada por: u = f (x1,x2…xn) = f (x) siendo x un vector columna perteneciente Rn designando con ∆(xi) = ∆xi a los errores absolutos de las variables x1,x2…xn y con ∆(u) el error absoluto de la función u. │∆(u)│ = │f(x1 + ∆x1, x2 + ∆x2 …xn + ∆xn) – f (x1,x2…xn)│ Aplicando un desarrollo de Taylor y sólo considerando las derivadas primeras, tenemos: ∆(u) ≈ n ∑ i =1 ∂f Δxi ∂xi n │∆(u)│= │ ∑ i =1 ∂f Δxi │≤ ∂xi n ∂f ∑ ∂x i =1 ⋅ Δxi i entonces la cota superior para ∆(u) queda expresada por: ∆*(u) = n ∂f ∑ ∂x i =1 ⋅ Δ* xi Cota superior del error absoluto para la función u i y la cota superior del error relativo: ε*(u) = Δ* (u) = u n ∑ i =1 ∂f Δ* xi ⋅ ∂xi u Cota superior del error relativo para la función u Propagación de los errores Apunte creado por el Ing. Amiconi Diego Federico - 6 - Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata Se trata de determinar la influencia que los errores implícitos en los datos ejercen sobre el error del resultado, que en ciertos casos puede ser considerable. a) Suma y diferencia ∂f = ±1 ∂x1 ∂f =1 ∂x1 ∂f = ±1 ∂x 2 ∂f =1 ∂x 2 f(x1,x2) = x1 ± x2 ∆*f = ∂f ∂f ⋅ Δ* ( x1) + ⋅ Δ* ( x 2) ∂x1 ∂x 2 ∆*f = ∆*(x1) + ∆*(x2) Δ* ( x1 ± x 2) = Δ* f = Δ* ( x1) + Δ* ( x 2) Entonces, tanto para la suma como para la diferencia, la cota del error absoluto esta dada por la suma de las cotas de los errores absolutos de las variables independientes. b) Producto f(x1,x2) = x1 · x2 ∆*f = ∆*(x1·x2) = ∂f = x2 ∂x1 ∂f = x2 ∂x1 ∂f = x1 ∂x 2 ∂f = x1 ∂x 2 ∂f ∂f ⋅ Δ* ( x1) + ⋅ Δ* ( x 2) ∂x1 ∂x 2 ~ ~ Δ* (x1 ⋅ x 2 ) = x 2 ⋅ Δ* ( x1) + x 1 ⋅ Δ* ( x 2) Cota del error absoluto ~ ε * ( x1 ⋅ x 2) = Δ ( x1 ⋅ x 2) * ~ ~ x1⋅ x 2 ~ x2 = ~ ~ x1 ⋅ x 2 x1 ⋅ Δ* ( x1) + ~ ~ ⋅ Δ* ( x 2) x1 ⋅ x 2 Apunte creado por el Ing. Amiconi Diego Federico - 7 - Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata ε * ( x1 ⋅ x 2) = Δ* ( x1) ~ + Δ* ( x 2) ~ x1 x2 * * ε * ( x1 ⋅ x 2) = εε *(x ( x11) + ε *ε( x(x 2 )2) Cota del error relativo c) Cociente ∂f 1 = ∂x1 x 2 f(x1,x2) = ∂f 1 = ∂x1 x2 x1 x2 ∂f x1 = − ∂x 2 ( x 2 )2 ∂f x1 =− ∂x1 ( x 2 )2 ~ 1 x1 ∂f ∂f x1 ∆ f = Δ* ⎛⎜ ⎞⎟ = ⋅ Δ* (x 2 ) ⋅ Δ* ( x1) + ⋅ Δ* ( x 2) = ~ ⋅ Δ* ( x1) + − 2 ~ ∂ ∂ x x x 2 1 2 ⎝ ⎠ ⎛ ⎞ x2 ⎜ x 2⎟ ⎝ ⎠ * ~ ~ ~ x 2 ⋅ Δ* ( x1) + − x1 ⋅ Δ* (x 2 ) = ⎛~⎞ ⎜ x2 ⎟ ⎝ ⎠ = 2 ⎛~⎞ ⎜ x2 ⎟ ⎝ ⎠ ~ x1 ⎞ ⎟ = ⎝ x2 ⎠ ( ) ( x) ε * x1 x 2 = Δ x1 2 ~ ⎛ ⎞ ⎜ x2 ⎟ ⎝ ⎠ ~ ~ ~ x1 ~ ~ ⋅ x1 ~ x2 ( ) Cota del error absoluto 2 ~ ε * x1 x 2 = ε * (x1) + ε * ( x 2 ) ⎛~ ⎞ ⎜ x 2⎟ ⎝ ⎠ 2 ~ ~ x 2 ⋅ Δ* ( x1) + x 1 ⋅ Δ* (x 2 ) x2 = 2 x 2 ⋅ Δ* ( x1) + x1 ⋅ Δ* ( x 2 ) ∆*f = Δ* ⎛⎜ * ~ x 2 ⋅ Δ* (x1) + x1 ⋅ Δ* (x 2 ) x 2 ⋅ Δ* ( x1) = ~ ~ x1 ⋅ Δ* ( x 2 ) + x2 ⋅ x 1 Cota del error relativo Apunte creado por el Ing. Amiconi Diego Federico - 8 - ~ ~ x1 ⋅ x 2 = Δ* (x1) ~ x1 + Δ* (x 2 ) ~ x2 Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata Método Inverso Dada una cierta función que depende de las variables x1,x2,…,xn afectadas de error, y dado u=f (x1,x2,…,xn); se busca determinar los errores absolutos ∆(x1), ∆(x2),… ∆(xn) para obtener el resultado con una aproximación prefijada. Consideremos la función y = f ( x1, x 2,...xn ) donde ⎧ x1 ⎫ ⎪ x 2⎪ ⎪ ⎪ Son las variables independientes x=⎨ ⎬ que están afectadas de errores ⎪... ⎪ ⎪⎩ xn ⎪⎭ El objetivo consiste en calcular las cotas de los errores absolutos ∆*(xi) con (i=1,2,…n) de modo tal que nos permitan obtener el resultado de la función y = f(x1, x2,..xn), calculada en el punto (x̃1, x̃2,… x̃n) con una aproximación prefijada. De la fórmula general tenemos: n Δ* f = ∑ i =1 ∂f ∂f ∂f ∂f ⋅ Δ* ( x1) + ⋅ Δ* ( x 2 ) + ........ + ⋅ Δ* ( xi ) = ⋅ Δ* ( xn ) ∂x1 ∂x 2 ∂xi ∂xn de esta última fórmula veremos que una misma cota del error absoluto ∆*f puede ser obtenida por distintos conjuntos de valores numéricos de las cotas de error absoluto ∆*(xi); en consecuencia este problema no tiene solución única. Entonces para evitar el problema de no tener una única solución hacemos diferentes hipótesis. Hipótesis 1: Igualdad de efectos Los efectos producidos en f debido a las cotas de los errores absolutos ∆*(xi) con (i=1,2,…n) son todos iguales. La fórmula general es: Δ* f = ∂f ∂f ∂f ⋅ Δ* ( x1) + ⋅ Δ* ( x 2 ) + .... + ⋅ Δ* ( xn ) ∂x1 ∂x 2 ∂xn a al hacer la hipótesis de efectos iguales: ∂f ∂f ∂f ⋅ Δ* ( x1) = ⋅ Δ* ( x 2 ) = .... = ⋅ Δ* ( xn ) ∂x1 ∂x 2 ∂xn reemplazando b en a nos queda: Apunte creado por el Ing. Amiconi Diego Federico - 9 - b Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata Δ* f = n ⋅ ∂f ⋅ Δ* ( x1) ∂x1 * Δ* ( x1) = Δ f n⋅ ∂f ∂x1 generalizando: Δ* f ∂f n⋅ ∂xi Δ* ( xi ) = (i = 1, 2, ….n) Cota de error absoluto de la variable independiente xi y la cota del error relativo asociado a la variable independiente xi, es: ε * ( xi ) = Δ* ( xi ) = xi Δ* f (i = 1, 2, ….n) ∂f n ⋅ xi ⋅ ∂xi Hipótesis 2: Igualdad de cotas de los errores absolutos La formula general es: Δ* f = Cota de error relativo de la variable independiente xi. ∂f ∂f ∂f ⋅ Δ* ( x1) + ⋅ Δ* ( x 2 ) + .... + ⋅ Δ* ( xn ) ∂x1 ∂x 2 ∂xn a al hacer la hipótesis de cotas de los errores absolutos iguales: Δ* ( x1) = Δ* ( x 2 ) = ..... = Δ* ( xn ) b Reemplazando b en a: ⎧ ∂f ∂f ∂f ⎫ * Δ* f = ⎨ + + ..... + ⎬ ⋅ Δ (x1) ∂xn ⎭ ⎩ ∂x1 ∂x 2 Despejando tenemos: Δ* ( x1) = Δ* f ⎧ ∂f ∂f ∂f ⎫ + + ..... + ⎨ ⎬ ∂xn ⎭ ⎩ ∂x1 ∂x 2 Generalizando: Cota del error absoluto de la Δ* f ( i = 1,2,…n) variable independiente xi. n ∂f ∑ j =1 ∂xj y la cota del error relativo asociado a la variable xi, es: Δ* (xi ) = Δ* ( xi ) ε (xi ) = = xi * Δ* f n xi ⋅ ∑ j =1 ∂f ∂xj (i = 1,2,…n) Cota del error relativo de la variable independiente xi. Apunte creado por el Ing. Amiconi Diego Federico - 10 - Cátedras de Modelos Numéricos, Análisis Numérico y Cálculo Avanzado U.T.N. Facultad Regional La Plata Hipótesis 3: Igualdad de las cotas de los errores relativos La fórmula general es: ∂f ∂f ∂f ⋅ Δ* ( x1) + ⋅ Δ* ( x 2 ) + .... + ⋅ Δ* ( xn ) ∂x1 ∂x 2 ∂xn Δ* f = a al hacer la hipótesis de las cotas de los errores relativos iguales: ε * (x1) = ε * ( x 2 ) = ε * ( x3 ) = ..... = ε * ( xn ) ó Δ* (x1) Δ* ( x 2 ) Δ* ( x3 ) Δ* ( xn ) = = = ...... = x1 x2 x3 xn b de la fórmula general a: Δ* f = ∂f Δ* (x1) ∂f Δ* ( x 2 ) ∂f Δ* (xn ) ⋅ x1 ⋅ + ⋅ x2 ⋅ + ......... + ⋅ xn ⋅ ∂x1 x1 ∂x 2 x2 ∂xn xn ε * ( x1) ε * (x 2 ) ε * (xn ) ⎧ ∂f ⎫ ∂f ∂f Δ* f = ⎨ ⋅ x1 + ⋅ x 2 + .... + ⋅ xn ⎬ ⋅ ε * ( x1) ∂x 2 ∂xn ⎩ ∂x1 ⎭ despejando: ε * (x1) = Δ* f ∂f ∂f ∂f ⋅ x1 + ⋅ x 2 + .... + ⋅ xn ∂x1 ∂x 2 ∂xn = Δ* f n ∂f xj ∑ j =1 ∂xj Generalizando: Δ* f Cota del error relativo (i = 1,2,….n) asociada a la variable xi. n ∂f x j ∑ j = 1 ∂xj y la cota del error absoluto asociado a la variable xi, es: ε * (xi ) = Δ ( xi ) = ε ( xi ) ⋅ xi = * xi ⋅ Δ* f * n ∂f ∑ ∂x j =1 (i = 1,2,….n) ⋅ xj j Apunte creado por el Ing. Amiconi Diego Federico - 11 - Cota del error absoluto asociada a la variable xi.