Integrales o Antiderivada Apuntes de análisis y cálculo
Anuncio

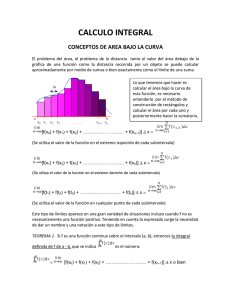
Integrales o Antiderivada Apuntes de análisis y cálculo Introducción Consideraremos una función real continua y derivable y = f(x) positiva y acotada, definida en el intervalo cerrado [a, b], entonces: f F x ' Se llama integral definida de la función f(x) 0 entre a y b (los límites de integración), al área de la porción de plano limitada por la gráfica de la función (figura 1), el eje X y las rectas paralelas x = a y x = b. Figura 1. Si f es derivable entonces su derivada existe. Esta ultima se puede diferenciar y existe una operación inversa a la diferenciación que se denomina antiderivada o integración. Así una función es integrable en un intervalo I si es diferenciable en ese intervalo. Sea entonces dy dx f ' y f x diferenciable (o derivable) entonces y ' f ' x o equivalentemente x de donde dy f y la integración denotado por el símbolo ' x dx dy: diferencial de y en términos de x dx: diferenciación , son operaciones inversas y se tiene que: dy f x dx ' y f ' de donde x dx Considerando el lado derecho de la igualdad y teniendo presente que la derivación e integración son operaciones inversas, se tiene que: y f x dx f x ' Así entonces: f x dx Ejemplo: F x F ' x f x f x sen x f ' x cos dy x pero y sen x, luego cos x dx dy cos x dx y cos x dx y sen x f x Suma de Riemann Una forma de encontrar el área S de la superficie limitada por la curva y = f (x), entre el eje x y las rectas que pasan por los puntos x = a y x = b, que son paralelas al eje “y”, es dividir el intervalo [a, b] en n partes. Figura 2. Figura 3. Denotándose la longitud de la primera parte como x1, la segunda como x2, y así sucesivamente hasta la última, xn. En cada parte se elegen los números x1, x2, ..., xn, y se escribe la suma Sn es evidentemente igual a la suma de las áreas de los rectángulos de la figura 2. Cuanto más fina sea la subdivisión del segmento [a, b], más próxima se encontrará Sn al área S (figura 3). Si se considera una sucesión de tales valores por división del intervalo [a, b] en partes cada vez más pequeñas, entonces la suma Sn tenderá a S. Suponiendo no sólo que n crece indefinidamente, sino también que xi tiende a cero. Así: Tipos de aproximación de la integral Suma inferior de Riemann (punto izquierdo): se toma como valor i el límite inferior del subintervalo, es decir, i -1. Gráficamente: Suma superior de Riemann (punto derecho): se toma como valor i el límite superior del subintervalo, es decir, i. Gráficamente: Suma de Riemnan (punto medio): se toma como valor i el punto medio entre los límites del subintervalo, es decir, (i -1 + i) / 2. Gráficamente: Integral definida El límite anterior se llama integral definida o integral de Riemann de la función f (x) en el intervalo [a, b], y se nota por: La expresión f (x)dx se llama integrando; a y b son los límites de integración; a es el límite inferior, y b, el límite superior. Primer teorema fundamental del cálculo infinitesimal Sea f integrable y continua sobre el intervalo [a, b] entonces: F x f x ' o d x f x dx f x a dx luego F es derivable en “x”, y: Segundo teorema fundamental del cálculo infinitesimal Si f es integrable sobre [a, b] y f = F' para alguna función F, entonces Esta igualdad es la famosa fórmula de Newton y Leibnitz, que reduce el problema de calcular la integral definida de una función a la obtención de una primitiva de la misma, y constituye así un enlace entre el cálculo diferencial y el integral. La diferencia se acostumbra a escribirse así: Ejemplo: La igualdad muestra que la función x3/3 es una primitiva de la función x2. Así, por la fórmula de Newton y Leibnitz, Propiedades de la integral definida Si f (x) y g(x) son continuas en el intervalo de integración [a, b]: 1. 2. 3. , siendo c una constante 4. 5. , cuando a < c < b 6. Primer teorema del valor medio: , para al menos un valor x = x0 entre a y b. 7. Si , se verifica . Integrales indefinidas; técnica de integración. Una función f (x) cuya derivada, en un cierto intervalo del eje x, F'(x) = f (x), se donde f (x) es la primitiva o integral indefinida de f (x). La integral indefinida de una función no es única. Todas las primitivas de f (x) =2x están representadas por la expresión x2 + C, en la que C es una constante cualquiera y que se denomina constante de integración. La primitiva o integral indefinida de la función f (x) se representa por medio del símbolo Propiedades de la integral indefinida d 1º dx d f x dx f x dx d 2º dx f x dx 3º a f x dx 4º f x Ejemplo: f x f x dx F x C a f x dx g x dx f x dx caso part icular a:cte . R g x dx xC 8 x 3 6 x 1 3 1 2 dx 8 x dx 6 x dx 2 x 8 x 4 6 4 2x 4x 4 x 3 2 3 2 x 1 c x TABLA DE INTEGRALES 1 3 2 x 1 c 2 dx