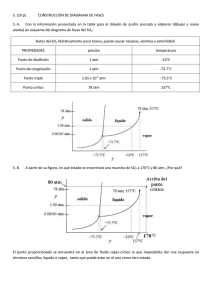
Ejercicio 6: Las fracciones molares de los componentes principales del aire seco a nivel del mar son xN2 =0.78, xO2 =0.21, xAr =0.0093, xCO2 =0.0004. (a) Encuentre la presión parcial de cada uno de estos gases en aire seco a 1.00 atm y 20 ° C. (b) Encuentre la masa de cada uno de estos gases en una habitación de 15 pies X 20 pies X 10 pies a 20 ° C si el barómetro lee 740 torr y la humedad relativa es cero. También, encuentra la densidad del aire en la habitación. (c) ¿Cuál tiene mayor masa, usted o el aire en la sala de este problema? ρ= (a) P=xP PxN2 =0.78(1 atm) = 0.78atm 𝑚 V ρ=1.1721Kg/𝑚^3 PxO2 =0.21atm PxAr =0.0093atm PxCO2 =0.0004. 𝑃𝑉 (b) 𝑛 = 𝑅𝑇 𝑛= 98,658.28𝑝𝑎 ∗ 84.9505𝑚3 = 3,438.5763𝑚𝑜𝑙 𝑝𝑎𝑚3 8.3144 ∗ 293.15𝐾 𝑚𝑜𝑙𝐾 𝑚𝑁2 = 𝑛 ∗ 𝑥𝑁2 ∗ 28.0134𝑔 = 75.1344𝐾𝑔 𝑚𝑜𝑙 𝑚𝑁2 = 𝑛 ∗ 𝑥𝑁2 ∗ 31.9988𝑔 = 23.1063𝐾𝑔 𝑚𝑜𝑙 𝑚𝑁2 = 𝑛 ∗ 𝑥𝑁2 ∗ 39.948𝑔 = 1.2775𝐾𝑔 𝑚𝑜𝑙 𝑚𝑁2 = 𝑛 ∗ 𝑥𝑁2 ∗ 44.0095𝑔 = 0.0605𝐾𝑔 𝑚𝑜𝑙 Ejercicio 7: Un gas hipotético obedece la ecuación del estado PV = nRT (1- aP), donde a es una constante. Para este gas: (a) demuestre que α = 1 / T y κ = 1 / P (1 + aP); (b) verifique que (∂P / ∂T) V = α / κ. V= nRT(1 + aP)/P dV/dP=-nRT/𝑃2 = (-PV/(1+aP))/ 𝑃2 dV/dT= nR(1 + aP)/P K=-(1/V)dV/dP=1/P(1+aP) dV/dT=V/T a=(1/V)(dV/dT)=1/T