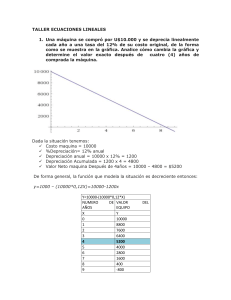
TALLER ECUACIONES LINEALES 1. Una máquina se compró por U$10.000 y se deprecia linealmente cada año a una tasa del 12% de su costo original, de la forma como se muestra en la gráfica. Analice cómo cambia la gráfica y determine el valor exacto después de cuatro (4) años de comprada la máquina. Dada la situación tenemos: Costo maquina = 10000 %Depreciación= 12% anual Depreciación anual = 10000 x 12% = 1200 Depreciación Acumulada = 1200 x 4 = 4800 Valor Neto maquina Después de 4años = 10000 – 4800 = $5200 De forma general, la función que modela la situación es decreciente entonces: y=1000 – (10000*0,12X)=10000-1200x Y=10000-(10000*0,12*X) NUMERO DE VALOR AÑOS EQUIPO X Y 0 10000 1 8800 2 7600 3 6400 4 5200 5 4000 6 2800 7 1600 8 400 9 -800 DEL La función lineal es decreciente, en donde la y refleja el valor de la máquina y las x reflejan los años de depreciación, por tal motivo a medida que aumenta el número de años, se reduce el valor de la máquina, la gráfica se intersecta en el eje y cuando x=0 y = 10000 y se intersecta en el eje de la x cuando y=o, x= 8.33 Véase: 10000-1200x = 0, x=10000/1200=8,33 De acuerdo con la tabla el valor de la maquina en el cuarto año es de $5200 2. Un fabricante de herramientas encuentra que sus ventas siguen la gráfica que se muestra. La variable x corresponde a la cantidad de martillos que debe vender, y el eje y corresponde al precio por cada martillo, según la cantidad. Determine cuál es el precio se producen 2500 martillos Hallamos la pendiente de la recta m= m= m= 𝒚𝟐 − 𝒚𝟏 𝒙𝟐 − 𝒙𝟏 (2750 − 2000 (2000 − 3000) -0,75 Usamos la ecuación pendiente intercepto 𝑦 − 𝑦0 = 𝑚(𝑥 − 𝑥0 ) 𝑦 − 2000 = −0,75(𝑥 − 3000) 𝑦 = −0,75𝑥 + 2250 + 2000 𝒚 = −𝟎, 𝟕𝟓𝒙 + 𝟒𝟐𝟓𝟎 Cuando producimos 2500 martillos el precio se determina reemplazando x en la ecuación: 𝒚 = −𝟎, 𝟕𝟓(𝟐𝟓𝟎𝟎) + 𝟒𝟐𝟓𝟎 𝒚 = 𝟐𝟑𝟕𝟓 , el precio es de $2375 cuando se producen 2500 martillos.