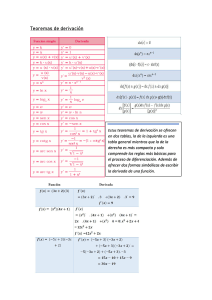
DERIVACIÓN IMPLÍCITA A continuación veremos en que consiste la derivación implícita. Hasta ahora hemos derivado funciones explícitas como 𝑦 = √𝑥 2 + 1 𝑥 2 −1 3 𝑌 = (𝑥 2 +1) o A continuación encontraremos la derivada de funciones implícitas del tipo 𝑥 2 + 𝑦 2 = 36 √𝑥 + √𝑦 = 1 o En este tipo de funciones en ocasiones es posible resolver para y como una función de x. Sin embargo, lo que se busca es encontrar la derivada de y con respecto de x, para ello se aplica el método de derivación implícita. El método consiste en derivar a los miembros de la ecuación con respecto a x, a continuación 𝑑𝑦 se despeja 𝑑𝑥 Ejemplo 1. Encontrar 𝑑𝑦 𝑑𝑥 por derivación implícita 4𝑥 2 + 9𝑦 2 = 36 Solución Derivando ambos miembros de la igualdad, se tiene 𝑑 𝑑𝑥 4 (4𝑥 2 + 9𝑦 2 ) = 𝑑 𝑑𝑥 (𝑥 2 ) + 9 𝑑 𝑑𝑥 𝑑 𝑑𝑥 (36) (𝑦 2 ) = 0 Como y es una función de x, se aplica la regla de la cadena para obtener 9 𝑑 𝑑𝑥 (𝑦 2 ) = 9 𝑑 𝑑𝑦 Despejando 𝑑𝑥 = − 8𝑥 18𝑦 𝑑𝑦 𝑑𝑥 = 9(2𝑦) 8𝑥 + 18𝑦 Por tanto 𝑑𝑦 (𝑦 2 ) 𝑑𝑦 𝑑𝑥 resulta = − 4𝑥 9𝑦 𝑑𝑦 𝑑𝑥 =0 𝑑𝑦 𝑑𝑥 = 18𝑦 𝑑𝑦 𝑑𝑥