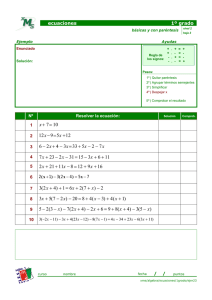
Los 10 casos de Factorización Expresiones Algebraicas "Común" significa que están o que pertenecen a todos. De tal manera que factor común tiene el significado de la(s) cantidad(es) que aparece multiplicando en todos los términos de la expresión. Regla: Se localizan y se escriben todos los factores comunes en su máxima expresión, a continuación un paréntesis y adentro de él lo que queda de la expresión original. Ejemplo: 4a 2b + 6abx 5= 2ab(2a + 3x 5) El proceso consiste en agrupar términos en cantidades iguales (de dos en dos, o de tres en tres, etc.), para luego factorizar cada grupo por factor común y finalmente volver a factorizar por factor común, en donde el paréntesis que debe quedar repetido en cada grupo es el factor común. Regla: el signo del primer término de cada grupo es el signo que debe ponerse en cada factorización por factor común. Ejemplo: 2ac + bc + 10a + 5b = c(2a + b) + 5(2a + b) Existe trinomio cuadrado perfecto cuando el primero y el tercer termino son raíces cuadradas exactas, y su segundo debe ser el doble producto de las raíces cuadradas de los términos cuadrados perfectos. Regla: Para resolverlo sacamos las raíces del primer y el tercer término y se forma una resta de las dos raíces elevado al cuadrado. Ejemplo: x 2+ 6x +9 = (x+3) 2 X 3 2.x.3=6x Se lo utiliza cuando hay un binomio y sus dos términos son cuadrados perfectos y están separados por una resta. Regla: Una diferencia de cuadrados se factoriza en dos binomios conjugados, formados con las raíces cuadradas de los términos originales. Ejemplo: 4a 2 - x 6= (2a + x 3)(2a - x 3) Se lo utiliza cuando tenemos un trinomio y su segundo termino no es el resultado que da cuando se multiplica duplo de la raíz cuadradada del primero y el tercero. Regla: Al comprobar que no es un trinomio cuadrado perfecto realizando la Multiplicación del duplo de la primera raíz por el tercer término. Procedemos a Agregamos un término y sumamos y restamos con el término para obtener el resultado Ejemplo: 4 2 x + 3x +4 = +x -x (x 4+ 4x 2 + 4) - x2 (x + 2) - x 2 [(x 2 + 2) – x] [(x2 +2) – x] ( x2 + 2 + x ) ( x 2 + 2 – x ) ( x 2+ x + 2 ) ( x2 + x – 2 ) X4 + 3x 2 + 4 = (x2 - x + 2 ) ( x 2 - x + 2) Estos trinomios tienen que tener una sola equis cuadrada. La letra b representa en general a cualquier número que vaya junto a la x ; y la c representa a cualquier número que vaya sin la x. Regla: Para factorizar un trinomio de la forma x22+ bx + c , se buscan dos números que sumados den b y multiplicados den c. Estos números hallados se colocan cada uno en un paréntesis. Ejemplo: x2 + bx + c = (x+3)(x+2) La diferencia de esta forma con la anterior es que en ésta debe haber más de una. La letra a representa un número que vaya junto a la x 2 (indica cuántas equis cuadradas hay); la letra b representa a cualquier número que vaya junto a la x ; y la c representa a cualquier número que vaya sin la x . Regla: Para factorizar se multiplica y se divide el trinomio por el coeficiente del 1er término, se resuelve el producto del primero y tercer término dejando Indicado el segundo término, se factoriza como el caso de trinomio de la forma x + bx + c , o sea, se buscan dos números que multiplicados y sumados den lo mismo, y se factoriza los binomios resultantes sacándoles Factor común. Luego se descompone el denominador y por ultimo dividimos Ejemplo: 15x - 23x + 4 15 ( 15x 4 - 23x 2+4 ) 15 (15x2 ) 2- - 23 (15x) + 60 (15x2 - 20) (15x2– 3 ) 15 5 (3x -4) 3(5x -1) 5.3 15x - 23x + 4 = (3x -4) (5x -1) La diferencia de esta forma con la anterior es que en ésta debe haber más de una. La letra a representa un número que vaya junto a la x (indica cuántas equis cuadradas hay); la letra b representa a cualquier número que vaya junto a la x ; y la c representa a cualquier número que vaya sin la x . 3 3 2 2 3 3 2 2 3 ( a + b ) = a + 3 a b + 3 ab + b 3 ( a - b ) = a - 3 a b + 3 ab - b Esta diferencia se da cuando tenemos dos términos y estos tiene raíces cubicas. Regla: Una diferencia de cubos se factoriza en dos factores. El primer factor es un binomio formado con la resta de las raíces cúbicas de los términos; el segundo factor es un trinomio que se forma a partir del factor anterior de la siguiente manera: Y Cuadrado del primer término (del primer factor antes obtenido); Y más el producto del primer término (del factor anterior) por el segundo; Y más el cuadrado del segundo término (del factor anterior). Ejemplo: a3 -1 = (a-1) (a 2+ a + 1) Siempre son dos términos sumados o restados que tienen raíz quinta, séptima u otra raíz impar Regla: Abrir dos pares de paréntesis, en el primer paréntesis sacar raíz de ambos términos y en el segundo paréntesis poner un polinomio donde el primer término vaya decreciendo y el segundo término vaya creciendo. Si es una suma, el polinomio es de signos intercalados Si es una resta, el polinomio es de signos positivos. Ejemplo: X 5 + y 5= (x + y) (x 4 -x 3 y + x 2y 2- xy 3 +y 4 )