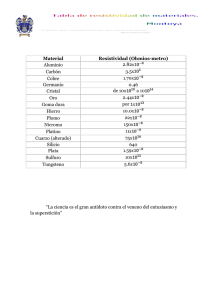
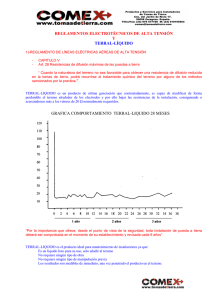
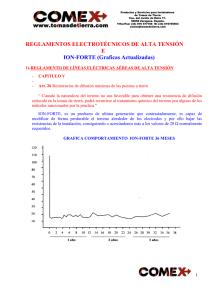
Diseño de Sistemas de Puesta a Tierra: Tesis de Ingeniería Eléctrica
Anuncio

UNIVERSIDAD POLITÉCNICA SALESIANA SEDE CUENCA CARRERA DE INGENIERÍA ELÉCTRICA Trabajo de titulación previo a la obtención del título de Ingeniero Eléctrico PROYECTO TÉCNICO INVESTIGATIVO: DISEÑO Y DETERMINACIÓN DE SISTEMAS DE PUESTA A TIERRA MEDIANTE PRUEBAS DE CAMPO CON ELEMENTOS COMUNES UTILIZADOS EN LA REGIÓN, INCLUYENDO GEM Y ELECTRODO QUÍMICO AUTOR: FREDDY MAURICIO SINCHI SINCHI TUTOR: ING. HERNÁN PATRICIO GUILLÉN COELLO Cuenca - Ecuador 2017 CESIÓN DE DERECHOS DE AUTOR Maniesto mi voluntad y cedo a la Universidad Politécnica Salesiana la titularidad sobre los derechos patrimoniales en virtud de que soy autor del trabajo de titulación DISEÑO Y DETERMINACIÓN DE SISTEMAS DE PUESTA A TIERRA MEDIANTE PRUEBAS DE CAMPO CON ELEMENTOS COMUNES UTILIZADOS EN LA REGIÓN, INCLUYENDO GEM Y ELECTRODO QUÍMICO, mismo que ha sido desarrollado para optar por el título de Ingeniero Eléctrico en la Universidad Politécnica Salesiana, quedando la Universidad facultada para ejercer plenamente los derechos cedidos anteriormente. En aplicación a lo determinado en la Ley de Propiedad Intelectual, en mi condición de autor me reservo los derechos morales de la obra antes citada. En concordancia, suscribo este documento en el momento que hago la entrega del trabajo nal en formato impreso y digital a la Biblioteca de la Universidad Politécnica Salesiana. Cuenca, julio de 2017 I CERTIFICACIÓN Yo declaro que bajo mi tutoría fue desarrollado el trabajo de titulación: DISEÑO Y DETERMINACIÓN DE SISTEMAS DE PUESTA A TIERRA MEDIANTE PRUEBAS DE CAMPO CON ELEMENTOS COMUNES UTILIZADOS EN LA REGIÓN, INCLUYENDO GEM Y ELECTRODO QUÍMICO realizado por: Freddy Mauricio Sinchi Sinchi obteniendo el Proyecto Técnico Investigativo, que cumple con todos los requisitos estipulados por la Universidad Politécnica Salesiana. Cuenca, julio de 2017 II DECLARATORIA DE RESPONSABILIDAD Yo Freddy Mauricio Sinchi Sinchi, autor del trabajo de titulación DISEÑO Y DETERMINACIÓN DE SISTEMAS DE PUESTA A TIERRA MEDIANTE PRUEBAS DE CAMPO CON ELEMENTOS COMUNES UTILIZADOS EN LA REGIÓN, INCLUYENDO GEM Y ELECTRODO QUÍMICO, certico que el total contenido de este Proyecto Técnico Investigativo es de mi exclusiva responsabilidad y autoría. Cuenca, julio de 2017 III DEDICATORIA A Dios, por darme sabiduría y cuidarme durante todo mi camino. A mi madre Yolanda, por ser una persona ejemplar y con sus consejos enseñarme a ser una persona de bien. A mis seres queridos que me han apoyado en mi trayecto profesional, Sandra, Alejandro, y a mis hermanos Xavier y Johanna. A mi padre Celso, que siempre está en mi corazón brindándome su amor, siempre te recordaré padre querido. FREDDY IV AGRADECIMIENTOS Mis más sinceros agradecimientos al Ing. Hernán Guillén y al Ing. Flavio Quizhpi, que gracias a sus conocimientos y experiencia me supieron orientar de la mejor manera para culminar este proyecto. A mis compañeros de clases por mantener una amistad de respeto y duradera. FREDDY V RESUMEN En este proyecto se realizan diseños de sistemas de puesta a tierra partiendo de mediciones de la resistividad en diferentes terrenos, se modela cada uno con la ecuación de suelo uniforme y mediante el método gráco Sunde. Con la resistividad de cada terreno, se realizan diseños de puestas calculando su resistencia con las ecuaciones de Schwarz, Dwight, y con la incorporación de fórmulas modicadas. Se implementa cada diseño calculado y se mide la resistencia de puesta a tierra mediante los métodos de dos puntos, caída de potencial y clamp-on. Se utiliza mejorador de tierra GEM en los diseños implementados, así como la implementación de un electrodo químico en un terreno de alta resistividad. Finalmente se presentan diseños de puesta a tierra que se pueden utilizar en la práctica. VI ABSTRACT In this project designs of grounding systems of the measurements of resistivity in dierent soils are made, each one is modeled with the uniform soil equation and by the Sunde graphic method. With the resistivity of each soil, lay designs are calculated by calculating their resistance with the Schwarz equations, Dwight, and with the incorporation of modied equations. Each calculated design is implemented and ground resistance is measured using the two-point, fall-of-potential and clamp-on methods. GEM soil treatment is used in the implemented designs, as well as the implementation of a chemical electrode in a high resistivity soil. Finally, there are grounding designs that can be used in practice. VII Índice general INTRODUCCIÓN 1 1. SISTEMAS DE PUESTA A TIERRA 3 1.1. Sistema de puesta a tierra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.2. Resistividad del terreno 3 1.2.1. 1.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Medición de la resistividad del terreno . . . . . . . . . . . . . . . . . . . . . 3 1.2.1.1. Método de tres puntos . . . . . . . . . . . . . . . . . . . . . . . . . 4 1.2.1.2. Método de cuatro puntos 5 . . . . . . . . . . . . . . . . . . . . . . . 1.2.2. Interpretación de las mediciones . . . . . . . . . . . . . . . . . . . . . . . . 7 1.2.3. Modelo de terreno uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.2.4. Modelo de terreno de dos capas por el método gráco . . . . . . . . . . . . 7 Diseño del sistema de puesta a tierra . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.3.1. Paso 1: Área de estudio 1.3.2. Paso 2: Conductor 1.3.3. Paso 3: Tensiones tolerables . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.3.4. Paso 4: Diseño Básico 12 1.3.5. Paso 5: Resistencia a tierra 1.3.2.1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 Cálculo del calibre del conductor . . . . . . . . . . . . . . . . . . . 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.3.5.1. Ecuación general . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.3.5.2. Ecuaciones de Schwarz 13 1.3.5.3. Ecuacion de Dwight . . . . . . . . . . . . . . . . . . . . . . . . . 15 1.3.5.4. Ecuaciones adicionales . . . . . . . . . . . . . . . . . . . . . . . . . 15 . . . . . . . . . . . . . . . . . . . . . . . . IG . . . . . (GP R). 1.3.6. Paso 6: Corriente máxima de malla 1.3.7. Paso 7: Potencial Máximo de la Malla 1.3.8. Paso 8: Tensión de paso y de contacto reales 1.3.9. Paso 9 y Paso 10: Control de seguridad 1.3.10. Paso 11: Acciones de Mejora 1.5. Tratamiento del terreno 18 . . . . . . . . . . . . . . . . 18 . . . . . . . . . . . . . . . . . 19 . . . . . . . . . . . . . . . . . . . . 21 . . . . . . . . . . . . . . . . . . . . . . . . . . 21 1.3.11. Paso 12: Poner a tierra todos los equipos 1.4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 1.4.1. Ingredientes de LRM 1.4.2. Requisitos básicos para LRM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.4.3. Conductividad de LRM 23 . . . . . . . . . . . . . . . . . . . . . . . . . . 23 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 1.4.4. Rendimiento a Largo Plazo del LRM . . . . . . . . . . . . . . . . . . . . . . 24 1.4.5. Método de construcción de LRM . . . . . . . . . . . . . . . . . . . . . . . . 24 1.4.5.1. Método llenado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 1.4.5.2. Método de penetración 1.4.5.3. Método de la zanja Resistencia de Puesta a Tierra . . . . . . . . . . . . . . . . . . . . . . . . 25 . . . . . . . . . . . . . . . . . . . . . . . . . . 25 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 1.5.1. Valor teórico de la resistencia a tierra . . . . . . . . . . . . . . . . . . . . . 26 1.5.2. Medición de la Resistencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 1.5.2.1. Método de dos puntos . . . . . . . . . . . . . . . . . . . . . . . . . 26 1.5.2.2. Método de tres puntos . . . . . . . . . . . . . . . . . . . . . . . . . 28 1.5.2.3. Método de caída del potencial. . . . . . . . . . . . . . . . . . . . . 29 1.5.2.4. Método de Clamp-on 1.5.2.5. Método de caída de potencia/clamp-on . . . . . . . . . . . . . . . . . . . . . . . . . VIII . . . . . . . . . . . . . . . 29 31 1.5.2.6. Multímetro de puesta a tierra basado en computadora . . . . . . . 2. IMPLEMENTACIÓN DE SISTEMAS DE PUESTA A TIERRA 2.1. 32 34 Mediciones de campo de la resistividad . . . . . . . . . . . . . . . . . . . . . . . . . 34 2.1.1. Resultados de las mediciones de la resistividad del terreno . . . . . . . . . . 35 2.2. Modelado de los terrenos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 2.3. Diseño de sistemas de puesta a tierra . . . . . . . . . . . . . . . . . . . . . . . . . . 40 2.3.1. Área de estudio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 2.3.2. Conductor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 2.3.3. Tensiones Tolerables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 2.3.4. Diseños básicos y resistencia de puesta a tierra 2.3.5. Corriente máxima de malla 2.3.6. Potencial Máximo de la Malla (GPR) . . . . . . . . . . . . . . . . . . . . . 52 2.3.7. Tensiones de paso y de contacto reales . . . . . . . . . . . . . . . . . . . . . 53 2.3.8. Control de seguridad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 Tratamiento del terreno para reducir la resistividad . . . . . . . . . . . . . . . . . . 54 2.4.1. 54 2.4. 2.4.2. 2.4.3. 2.5. . . . . . . . . . . . . . . . . 42 . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 Material de mejora del suelo seco (GEM Cadweld) . . . . . . . . . . . . . . 2.4.1.1. Método de instalación . . . . . . . . . . . . . . . . . . . . . . . . . 55 2.4.1.2. Implementación del GEM Cadweld 55 . . . . . . . . . . . . . . . . . Material de mejora del suelo premezclado (GEM BenzoElectric) . . . . . . 58 2.4.2.1. Método de instalación . . . . . . . . . . . . . . . . . . . . . . . . . 59 2.4.2.2. Implementación del GEM BenzoElectric . . . . . . . . . . . . . . . Electrodo del tipo Químico . . . . . . . . . . . . . . . . . . . . . . . . . . . 60 63 2.4.3.1. Método de instalación . . . . . . . . . . . . . . . . . . . . . . . . . 63 2.4.3.2. Implementación del Electrodo Químico . . . . . . . . . . . . . . . 64 Medición de la resistencia de puesta a tierra . . . . . . . . . . . . . . . . . . . . . . 64 2.5.1. 65 Resultados de las mediciones . . . . . . . . . . . . . . . . . . . . . . . . . . 3. ANÁLISIS DE LOS RESULTADOS 72 3.1. Resultados de las tensiones tolerables . . . . . . . . . . . . . . . . . . . . . . . . . . 72 3.2. Resultados de la formulación utilizada . . . . . . . . . . . . . . . . . . . . . . . . . 72 3.3. Resultados de la adherencia del GEM con el terreno y las varillas . . . . . . . . . . 75 3.4. Resultados de la aplicación del GEM Cadweld . . . . . . . . . . . . . . . . . . . . . 76 3.5. Resultados de la aplicación del GEM BenzoElectric . . . . . . . . . . . . . . . . . . 77 3.6. Resultados de la aplicación del Electrodo Químico . . . . . . . . . . . . . . . . . . 77 3.7. Implementaciones para una resistencia de puesta a tierra de 15 ohmios . . . . . . . 78 4. CONCLUSIONES Y RECOMENDACIONES 82 4.1. CONCLUSIONES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 4.2. RECOMENDACIONES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 BIBLIOGRAFÍA 88 A. MODELO DEL SUELO POR EL MÉTODO GRÁFICO SUNDE 89 B. MÉTODO DE INSTALACIÓN DEL ELECTRODO QUÍMICO 122 C. TABLAS 124 D. MEDICIÓN DE LA RESISTENCIA POR EL MÉTODO DE CAÍDA DE POTENCIAL 128 E. DISEÑOS DE SISTEMAS DE PUESTA A TIERRA IX 133 Índice de guras 1.2.1.Diagrama del método de tres puntos [8]. . . . . . . . . . . . . . . . . . . . . . . . . 4 1.2.2.Curva de resistividad típica [6]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 1.2.3.Método de cuatro puntos: (a) picas equidistantes y (b) picas espaciadas de manera desigual [6]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 1.2.4.Gráca de Sunde [8]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.3.1.Coecientes k1 y k2 de la fórmula de Schwarz: (a) coeciente k1 , (b) coeciente k2 [8]. 14 1.3.2.Conguraciones de puesta a tierra: (a) unión de dos varillas, (b) unión de tres varillas y (c) unión de tres varillas en forma triangular. . . . . . . . . . . . . . . . . . . . . 1.4.1.Electrodo vertical cubierto con LRM [14]. . . . . . . . . . . . . . . . . . . . . . . . 1.4.2.Electrodo de tierra horizontal cubierto con LRM [14]. . . . . . . . . . . . . . . . . 16 22 23 1.4.3.Métodos de construcción usando LRM: (a) varilla vertical con el oricio relleno de LRM, (b) electrodo de tira, (c) se agrega LRM líquido y penetra en la tierra que rodea al electrodo incorporado, (d) una ranura anular excavado alrededor de una varilla vertical y luego se llena el LRM líquido, (e) método de la zanja que usa LRM para recubrir el electrodo horizontal y luego se rellena con tierra, (f ) método de la zanja usado en la construcción de un electrodo de tierra horizontal tipo placa [14]. 25 1.5.1.Medida de la resistencia de tierra a dos puntos utilizando un instrumento especializado de medición [4]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 1.5.2.Medida de la resistencia de tierra a dos puntos desde el cuadro de alimentación [4]. 27 1.5.3.Método de tres puntos [18]. 28 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.5.4.Método de caída del potencial [6]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 1.5.5.Medición de la resistencia mediante el método de clamp-on [6]. . . . . . . . . . . . 30 1.5.6.Medición incorrecta de la resistencia de tierra por el método clamp-on [6]. . . . . . 31 1.5.7.Medición de la resistencia de una torre utilizando el método de caída de potencial y mediciones de corriente de fuga [6]. . . . . . . . . . . . . . . . . . . . . . . . . . . 32 1.5.8.Medida de impedancia de tierra mediante multímetro de tierra basado en computadora [6]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.1.1.Telurómetro digital GP-2 Geo Test [17]. . . . . . . . . . . . . . . . . . . . . . . . . 2.1.2.Direcciones para las mediciones de las resistividades del terreno. . . . . . . . . . . 33 34 35 2.4.1.Mejorador de tierra GEM marca Cadweld [1]. . . . . . . . . . . . . . . . . . . . . . 55 2.4.2.Mejorador de tierra GEM marca BenzoElectric 58 . . . . . . . . . . . . . . . . . . . . 2.4.3.Excavación del agujero para la implementación del GEM. 2.4.4.Electrodo Químico de puesta a tierra marca Parres. . . . . . . . . . . . . . . 59 . . . . . . . . . . . . . . . . . 63 2.4.5.Agregado Electrolítico para electrodos de puesta a tierra. . . . . . . . . . . . . . . 64 2.5.1.Medidor de resistencia a tierra tipo Pinza. . . . . . . . . . . . . . . . . . . . . . . . 65 3.3.1.Compactibilidad: a) GEM premezclado y b) GEM en polvo . . . . . . . . . . . . . 76 A.0.1.Gráca de Sunde del terreno 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90 A.0.2.Curva de resistividad aparente del terreno 1. . . . . . . . . . . . . . . . . . . . . . 91 A.0.3.Gráca de Sunde del terreno 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92 A.0.4.Curva de resistividad aparente del terreno 2. . . . . . . . . . . . . . . . . . . . . . 93 A.0.5.Gráca de Sunde del terreno 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94 A.0.6.Curva de resistividad aparente del terreno 3. . . . . . . . . . . . . . . . . . . . . . 95 A.0.7.Gráca de Sunde del terreno 4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 A.0.8.Curva de resistividad aparente del terreno 4. 97 X . . . . . . . . . . . . . . . . . . . . . A.0.9.Gráca de Sunde del terreno 5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A.0.10. Curva de resistividad aparente del terreno 5. 98 . . . . . . . . . . . . . . . . . . . . . 99 A.0.11. Gráca de Sunde del terreno 6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100 A.0.12. Curva de resistividad aparente del terreno 6. . . . . . . . . . . . . . . . . . . . . . 101 A.0.13. Gráca de Sunde del terreno 7. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102 A.0.14. Curva de resistividad aparente del terreno 7. . . . . . . . . . . . . . . . . . . . . . 103 A.0.15. Gráca de Sunde del terreno 8. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104 A.0.16. Curva de resistividad aparente del terreno 8. . . . . . . . . . . . . . . . . . . . . . 105 A.0.17. Gráca de Sunde del terreno 9. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106 A.0.18. Curva de resistividad aparente del terreno 9. A.0.19. Gráca de Sunde del terreno 10. . . . . . . . . . . . . . . . . . . . . . 107 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108 A.0.20. Curva de resistividad aparente del terreno 10. . . . . . . . . . . . . . . . . . . . . . 109 A.0.21. Gráca de Sunde del terreno 11. 110 . . . . . . . . . . . . . . . . . . . . . . . . . . . . A.0.22. Curva de resistividad aparente del terreno 11. . . . . . . . . . . . . . . . . . . . . . 111 A.0.23. Gráca de Sunde del terreno 12. 112 . . . . . . . . . . . . . . . . . . . . . . . . . . . . A.0.24. Curva de resistividad aparente del terreno 12. . . . . . . . . . . . . . . . . . . . . . 113 A.0.25. Gráca de Sunde del terreno 13. 114 . . . . . . . . . . . . . . . . . . . . . . . . . . . . A.0.26. Curva de resistividad aparente del terreno 13. . . . . . . . . . . . . . . . . . . . . . 115 A.0.27. Gráca de Sunde del terreno 14. 116 . . . . . . . . . . . . . . . . . . . . . . . . . . . . A.0.28. Curva de resistividad aparente del terreno 14. . . . . . . . . . . . . . . . . . . . . . 117 A.0.29. Gráca de Sunde del terreno 15. 118 . . . . . . . . . . . . . . . . . . . . . . . . . . . . A.0.30. Curva de resistividad aparente del terreno 15. . . . . . . . . . . . . . . . . . . . . . 119 A.0.31. Gráca de Sunde del terreno 16. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120 A.0.32. Curva de resistividad aparente del terreno 16. . . . . . . . . . . . . . . . . . . . . . 121 XI Índice de tablas 1.1. Constantes de materiales [8]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.2. Valores típicos de Df [8]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 2.1. Valores de resistividad medidos en el terreno 1. . . . . . . . . . . . . . . . . . . . . 35 2.2. Valores de resistividad medidos en el terreno 2. . . . . . . . . . . . . . . . . . . . . 35 2.3. Valores de resistividad medidos en el terreno 3. . . . . . . . . . . . . . . . . . . . . 36 2.4. Valores de resistividad medidos en el terreno 4. . . . . . . . . . . . . . . . . . . . . 36 2.5. Valores de resistividad medidos en el terreno 5. . . . . . . . . . . . . . . . . . . . . 36 2.6. Valores de resistividad medidos en el terreno 6. . . . . . . . . . . . . . . . . . . . . 36 2.7. Valores de resistividad medidos en el terreno 7. . . . . . . . . . . . . . . . . . . . . 37 2.8. Valores de resistividad medidos en el terreno 8. . . . . . . . . . . . . . . . . . . . . 37 2.9. Valores de resistividad medidos en el terreno 9. . . . . . . . . . . . . . . . . . . . . 37 2.10. Valores de resistividad medidos en el terreno 10. . . . . . . . . . . . . . . . . . . . 37 2.11. Valores de resistividad medidos en el terreno 11. . . . . . . . . . . . . . . . . . . . 38 2.12. Valores de resistividad medidos en el terreno 12. . . . . . . . . . . . . . . . . . . . 38 2.13. Valores de resistividad medidos en el terreno 13. . . . . . . . . . . . . . . . . . . . 38 2.14. Valores de resistividad medidos en el terreno 14. . . . . . . . . . . . . . . . . . . . 38 2.15. Valores de resistividad medidos en el terreno 15. . . . . . . . . . . . . . . . . . . . 39 2.16. Valores de resistividad medidos en el terreno 16. . . . . . . . . . . . . . . . . . . . 39 . . . . . . . . . . . . . . . . . . . . . 39 2.18. Valores seleccionados de resistividad aparente de los terrenos. . . . . . . . . . . . . 40 2.17. Resultados del modelamiento de los terrenos. 2.19. Resumen durante la falla . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 2.20. Diseño del sistema de puesta a tierra para el terreno 1. . . . . . . . . . . . . . . . . 43 2.21. Diseños de sistemas de puesta a tierra para el terreno 2. . . . . . . . . . . . . . . . 43 2.22. Diseño del sistema de puesta a tierra para el terreno 3. . . . . . . . . . . . . . . . . 43 2.23. Diseños de sistemas de puesta a tierra para el terreno 4. . . . . . . . . . . . . . . . 44 2.24. Diseño del sistema de puesta a tierra para el terreno 5. . . . . . . . . . . . . . . . . 44 2.25. Diseño del sistema de puesta a tierra para el terreno 6. . . . . . . . . . . . . . . . . 44 2.26. Diseño del sistema de puesta a tierra para el terreno 7. . . . . . . . . . . . . . . . . 45 2.27. Diseños de sistemas de puesta a tierra para el terreno 8. . . . . . . . . . . . . . . . 45 2.28. Diseños de sistemas de puesta a tierra para el terreno 9. . . . . . . . . . . . . . . . 46 2.29. Diseños de sistemas de puesta a tierra para el terreno 10. . . . . . . . . . . . . . . 46 2.30. Diseños de sistemas de puesta a tierra para el terreno 11. . . . . . . . . . . . . . . 47 2.31. Diseños de sistemas de puesta a tierra para el terreno 12. . . . . . . . . . . . . . . 48 2.32. Diseños de sistemas de puesta a tierra para el terreno 13. . . . . . . . . . . . . . . 49 2.33. Diseños de sistemas de puesta a tierra para el terreno 14. . . . . . . . . . . . . . . 50 2.34. Diseños de sistemas de puesta a tierra para el terreno 15. . . . . . . . . . . . . . . 51 2.35. Diseños de sistemas de puesta a tierra para el terreno 16. . . . . . . . . . . . . . . 52 2.36. Datos para el cálculo de las tensiones de paso y de contacto reales. . . . . . . . . . 53 2.37. Datos para el cálculo de la tensión de paso y de contacto reales de la malla cuadrada del diseño T2.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 2.38. Implementación del GEM Cadweld en el terreno 8. . . . . . . . . . . . . . . . . . . 56 2.39. Implementación del GEM Cadweld en el terreno 14. . . . . . . . . . . . . . . . . . 57 2.40. Implementación del GEM Cadweld en el terreno 15. . . . . . . . . . . . . . . . . . 58 2.41. Implementación del GEM BenzoElectric en el terreno 2. . . . . . . . . . . . . . . . 60 2.42. Implementación del GEM BenzoElectric en el terreno 4. . . . . . . . . . . . . . . . 60 XII 2.43. Implementación del GEM BenzoElectric en el terreno 11. . . . . . . . . . . . . . . 61 2.44. Implementación del GEM BenzoElectric en el terreno 12. . . . . . . . . . . . . . . 61 2.45. Implementación del GEM BenzoElectric en el terreno 13. . . . . . . . . . . . . . . 62 2.46. Implementación del GEM BenzoElectric en el terreno 16. . . . . . . . . . . . . . . 62 2.47. Implementación del Electrodo Químico en el terreno 16. . . . . . . . . . . . . . . . 64 2.48. Mediciones de la resistencia del diseño implementado en el terreno 1. . . . . . . . . 65 2.49. Mediciones de la resistencia de los diseños implementados en el terreno 2. . . . . . 65 2.50. Mediciones de la resistencia de los diseños implementados en el terreno 3. . . . . . 66 2.51. Mediciones de la resistencia de los diseños implementados en el terreno 4. . . . . . 66 2.52. Mediciones de la resistencia del diseño implementado en el terreno 5. . . . . . . . . 66 2.53. Mediciones de la resistencia del diseño implementado en el terreno 6. . . . . . . . . 66 2.54. Mediciones de la resistencia de los diseños implementados en el terreno 7. . . . . . 67 2.55. Mediciones de la resistencia de los diseños implementados en el terreno 8. . . . . . 67 2.56. Mediciones de la resistencia de los diseños implementados en el terreno 9. . . . . . 67 2.57. Mediciones de la resistencia de los diseños implementados en el terreno 10. . . . . . 68 2.58. Mediciones de la resistencia de los diseños implementados en el terreno 11. . . . . . 68 2.59. Mediciones de la resistencia de los diseños implementados en el terreno 12. . . . . . 68 2.60. Mediciones de la resistencia de los diseños implementados en el terreno 13. . . . . . 69 2.61. Mediciones de la resistencia de los diseños implementados en el terreno 14. . . . . . 70 2.62. Mediciones de la resistencia de los diseños implementados en el terreno 15. . . . . . 70 2.63. Mediciones de la resistencia de los diseños implementados en el terreno 16. . . . . . 71 2.64. Mediciones de resistencia de puesta a tierra mediante 3 métodos. 71 . . . . . . . . . . 3.1. Resultados de las tensiones tolerables del diseño T2.3 . . . . . . . . . . . . . . . . . 72 3.2. Cálculos y mediciones para el diseño de una varilla. . . . . . . . . . . . . . . . . . . 73 3.3. Cálculos y mediciones para el diseño de dos varillas. 3.4. Cálculos y mediciones para el diseño de tres varillas en disposición lineal. 3.5. Cálculos y mediciones para el diseño de tres varillas en disposición triangular. . . . 75 3.6. Cálculos y mediciones para el diseño de mallas cuadradas. . . . . . . . . . . . . . . 75 3.7. Resultados mediante la aplicación del GEM Cadweld . . . . . . . . . . . . . . . . . 76 3.8. Resultados mediante la aplicación del GEM BenzoElectric . . . . . . . . . . . . . . 77 3.9. Diseños de sistemas de puesta a tierra para el terreno 16. 78 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74 74 3.10. Diseños implementados con varillas de 1.8m para una resistencia objetivo de 15 ohmios. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 3.11. Diseños implementados con varillas de 2.7m para una resistencia objetivo de aproximadamente 15 ohmios. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80 3.12. Diseños implementados con GEM Cadweld obteniendo una resistencia inferior a 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80 3.13. Diseños implementados con GEM BenzoElectric para una resistencia objetivo. . . . ohmios. 81 4.1. Diseños recomendados para obtener una resistencia de 15 ohm usando conductor 4.2. Diseños recomendados para obtener una resistencia de 15 ohm usando GEM Ben- 4.3. Diseños recomendados para obtener una resistencia de 15 ohm usando GEM Cadweld. 87 (horizontal) y varillas (vertical). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . zoElectric. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B.1. Método de instalación del Electrodo Químico [2]. . . . . . . . . . . . . . . . . . . . 85 86 123 C.1. Fórmulas para calcular la resistencia de puesta a tierra de distintas conguraciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125 C.2. Propiedades de los conductores [9]. . . . . . . . . . . . . . . . . . . . . . . . . . . . [11]. 126 C.3. Diagrama de bloques del procedimiento del diseño según el estándar IEEE 80-2013 [8]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127 D.1. Medición de la resistencia a tierra del diseño T1.1 por el método del 62 %. . . . . . 129 D.2. Medición de la resistencia a tierra del diseño T2.1 por el método del 62 %. . . . . . 129 D.3. Medición de la resistencia a tierra del diseño T3.1 por el método del 62 %. . . . . . 129 D.4. Medición de la resistencia a tierra del diseño T4.1 por el método del 62 %. . . . . . 129 XIII D.5. Medición de la resistencia a tierra del diseño T5.1 por el método del 62 %. . . . . . 130 D.6. Medición de la resistencia a tierra del diseño T6.1 por el método del 62 %. . . . . . 130 D.7. Medición de la resistencia a tierra del diseño T7.1 por el método del 62 %. . . . . . 130 D.8. Medición de la resistencia a tierra del diseño T8.1 por el método del 62 %. . . . . . 130 D.9. Medición de la resistencia a tierra del diseño T9.1 por el método del 62 %. . . . . . 131 D.10.Medición de la resistencia a tierra del diseño T10.1 por el método del 62 %. . . . . 131 D.11.Medición de la resistencia a tierra del diseño T11.1 por el método del 62 %. . . . . 131 D.12.Medición de la resistencia a tierra del diseño T12.1 por el método del 62 %. . . . . 131 D.13.Medición de la resistencia a tierra del diseño T13.1 por el método del 62 %. . . . . 132 D.14.Medición de la resistencia a tierra del diseño T14.1 por el método del 62 %. . . . . 132 D.15.Medición de la resistencia a tierra del diseño T15.1 por el método del 62 %. . . . . 132 D.16.Medición de la resistencia a tierra del diseño T16.1 por el método del 62 %. . . . . 132 E.1. Diseños recomendados para obtener una resistencia de 20 ohm usando conductor (horizontal) y varillas (vertical). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134 E.2. Diseños recomendados para obtener una resistencia de 20 ohm usando GEM BenzoElectric. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135 E.3. Diseños recomendados para obtener una resistencia de 20 ohm usando GEM Cadweld.136 E.4. Diseños recomendados para obtener una resistencia de 10 ohm usando conductor (horizontal) y varillas (vertical). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137 E.5. Diseños recomendados para obtener una resistencia de 10 ohm usando GEM BenzoElectric. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138 E.6. Diseños recomendados para obtener una resistencia de 10 ohm usando GEM Cadweld.139 XIV INTRODUCCIÓN La función del sistema de puesta a tierra (SPT) es garantizar la seguridad de las personas y protección de los equipos, eso hace que en todo diseño, se je una resistencia objetivo. En nuestro país, a veces por la premura del tiempo, se establecen diseños de puesta a tierra sin realizar un análisis de la 1 resistividad del terreno y de las normas que existen para su diseño. En la actualidad, varias empresas de distribución eléctrica como la Empresa Eléctrica de Quito S.A., Empresa Eléctrica Regional Centro Sur C.A., y Empresas Eléctricas de Colombia estudiadas en [12], toman un valor de referencia de máximo 25 ohmios para la resistencia de puesta a tierra, este valor que también se indica en el Código Eléctrico Nacional (NEC, por sus siglas en inglés) [9], se basa en la resistencia máxima para un solo 2 electrodo; y en el caso de obtener una resistencia mayor recomienda adicionar otro. Sin embargo, en la práctica, en muchas ocasiones no basta con dos electrodos para obtener el valor de resistencia deseada, por lo que se adicionan más electrodos de forma arbitraria sin un completo conocimiento de su efecto. De tal manera que puede resultar en un sobredimensionamiento del sistema de puesta a tierra, que involucra gastos innecesarios. Hoy en día existen fórmulas que permiten diseñar las conguraciones del SPT estimando ya el valor de la resistencia a ser esperada; sin embargo, esto no siempre se aplica debido a que se tienen muchas variables para el diseño y algunas pueden ser imprácticas o innecesarias. Como por ejemplo se conoce que con un gran incremento del radio del conductor, o con un incremento en su profundidad de enterramiento no se consiguen mejoras signicativas en el valor de resistencia de puesta a tierra [15]. En este proyecto se determinan diseños de puestas a tierra en base a la experiencia ganada a través de numerosas pruebas de campo, cálculos y mediciones. Usando materiales comunes en la práctica, existentes en la región, y su resultado será de gran utilidad cuando se necesite conocer un diseño práctico de puesta a tierra para obtener un valor de resistencia esperado, sin la necesidad de recurrir a programas complejos y con demasiadas variables. Además se pone en práctica los principales métodos de medición de la resistividad del terreno y de la resistencia de puesta a tierra. Este proyecto satisface la necesidad de la creación de una guía con diseños de SPT recomendados para los diferentes valores de resistividad del terreno que se pueden encontrar en la práctica, los diseños pueden incluir varillas y conductores, electrodo químico, o la implementación de un tratamiento del terreno para reducir la resistencia de puesta a tierra. Teniendo así, conguraciones y recomendaciones para una instalación a bajo costo, a la cual puedan acceder ingenieros, técnicos y estudiantes. 1 Indica que tanto se opone el terreno al paso de la 2 Es un cuerpo metálico conductor desnudo que va física. corriente eléctrica. enterrado y su función es establecer el contacto con la tierra 1 GRUPO OBJETIVO El resultado del presente proyecto servirá como una guía no solamente para estudiantes e ingenieros eléctricos, sino para toda persona que esté vinculada directa o indirectamente con el sector eléctrico, para conocer una manera práctica con elementos comunes de realizar una puesta a tierra y su importancia, y a su vez que puedan implementar el diseño que requieran; además los resultados de este proyecto servirá como una fuente de información para futuros proyectos en este campo. OBJETIVOS Objetivo general Establecer diseños de sistemas de puesta a tierra mediante pruebas de campo con elementos comunes utilizados en la región, GEM y electrodo químico. Objetivos especícos 1. Medir e identicar 16 terrenos con diferentes valores de resistividad. 2. Calcular, diseñar y determinar conguraciones de SPT para obtener una resistencia de 15 Ω en cada terreno. 3. Implementar las conguraciones de puesta a tierra, medir la resistencia y comprobar con el cálculo teórico. 4. Determinar la conabilidad entre los métodos de medición de resistencia por Caída de Tensión y mediante el equipo de medición Tipo Gancho. 5. Usar enriquecedor de tierra GEM (Benzoeletric y Elect. Cadweld) para medir y analizar el costo-benecio con respecto al diseño básico. 6. Implementar un electrodo químico para medir y analizar el costo-benecio con respecto al diseño básico. 7. Denir el diseño básico de puesta a tierra para los diferentes rangos de resistividad e indicar el diseño alternativo usando enriquecedor de tierra GEM y Electrodo Químico. 8. Realizar un programa computacional donde se muestre la conguración de puesta a tierra al ingresar la resistividad del terreno y la resistencia que desea obtener, indicando además las consideraciones y/o conguraciones usando GEM y Electrodo Químico. 2 Capítulo 1 SISTEMAS DE PUESTA A TIERRA 1.1. Sistema de puesta a tierra Un sistema de puesta a tierra es la conexión intencional a tierra de los elementos conductores de un sistema eléctrico, con la nalidad de proporcionar los medios para disipar las corrientes eléctricas en la tierra en condiciones normales y de falla, sin exceder los límites de operación de los equipos, ni afectar adversamente la continuidad del servicio. Además, para asegurar que una persona cercana a instalaciones con conexión a tierra no esté expuesta al peligro de una descarga eléctrica crítica. 1.2. Resistividad del terreno Para el cálculo y diseño de sistemas de puesta a tierra es fundamental que se investigue la resistividad del terreno en la ubicación deseada de la conexión, ya que éste es el factor más importante en el fenómeno de conducción de la corriente en el terreno. No se recomienda estimar la resistividad basándose en la clasicación del terreno debido a que éstas dan solamente una aproximación de la resistividad. Por lo tanto, las mediciones de campo de la resistividad son imprescindibles. La resistividad del terreno no varía solamente con la profundidad sino también con factores como la composición del terreno, la concentración de sales solubles, el contenido de humedad, la granulometría, la estratigrafía, el efecto de la compactación y el efecto de la temperatura [17]. La interpretación de las mediciones de la resistividad del terreno puede variar considerablemente, especialmente cuando se encuentran terrenos con resistividades no uniformes, sólo en unos pocos casos, las resistividades del terreno son constantes con el aumento de la profundidad. Generalmente hay varias capas de tierra, cada una de las cuales tiene una resistividad diferente. También pueden ocurrir cambios laterales, pero en comparación con las capas verticales, estos cambios suelen ser más graduales y despreciables. 1.2.1. Medición de la resistividad del terreno Las mediciones de resistividad del terreno sirven especialmente para determinar si hay variaciones importantes con respecto a la profundidad. Los objetos enterrados como rieles y tuberías metálicas, situados en las proximidades del terreno que se está probando, pueden tener una inuencia considerable en los resultados de las mediciones. Siempre que se sospeche de la presencia de estructuras metálicas enterradas en el área donde se deben realizar mediciones de la resistividad del terreno y se conozca la ubicación de estas estructuras, se puede minimizar su inuencia alineando las picas auxiliares de prueba en una dirección perpendicular al enrutamiento de estas estructuras. 3 Entre los principales métodos para la medición de la resistividad del terreno están: 1.2.1.1. Método de tres puntos En el método de tres puntos o variación de la profundidad, se realizan varias mediciones de la resistencia de puesta a tierra en correlación con el incremento de profundidad de una varilla de tierra y se calcula la resistividad del terreno mediante la ecuación (1.2.1). Entonces, el valor de la resistencia medida reejará la 1 resistividad aparente para cada profundidad de la varilla. El diagrama del método de dos puntos se muestra en la Figura 1.2.1, donde se varía la profundidad Lr de la varilla accionada (E) situada en el terreno bajo prueba. Las dos picas auxiliares, se colocan en línea recta a poca profundidad. La posición de la pica de tensión varilla de prueba (E) y la pica de corriente (C) ρa = (P ) varía entre la [8]. La resistividad aparente está dada por 2πLr R ln( 8Ld r ) − 1 (1.2.1) Donde ρa es la resistividad aparente del terreno R es la resistencia medida Lr d [Ω · m] [Ω] es la longitud de la varilla es el diámetro de la varilla [m] [m] Este método proporciona información útil sobre la naturaleza del terreno (cinco a diez veces la longitud de la varilla). Para áreas grandes, varias ubicaciones de las varillas pueden dar una indicación de cambios laterales signicativos en la resistividad del terreno. Una desventaja de este método es que la varilla podría vibrar a medida que se acciona, resultando un contacto pobre con el terreno a lo largo de su longitud. Figura 1.2.1: Diagrama del método de tres puntos [8]. 1 Es la resistividad obtenida con una medida directa en el terreno natural. 4 1.2.1.2. Método de cuatro puntos Un buen método para medir la resistividad aparente de terrenos con una gran área es el método de cuatro puntos (Wenner). Se instalan cuatro picas auxiliares en la tierra, todas a la profundidad b y espaciadas (en línea recta) a intervalos exteriores, y el potencial V a. Se pasa una corriente de prueba I entre las dos picas entre las dos picas internas se mide con un potenciómetro o voltímetro V I da la resistencia R en ohms. El método de cuatro puntos obtiene los datos de resistividad aparente del terreno para capas de alta impedancia. Entonces, la relación más profundas sin conducir las picas de prueba a esas capas. No se necesita equipo pesado para realizar la prueba de cuatro puntos. A menudo se usan dos variantes diferentes de este método: Igualmente Espaciado o Arreglo Wenner Con esta disposición, las picas están igualmente separadas, como se muestra en la Figura 1.2.3 (a). Siendo a la distancia entre dos picas adyacentes. Entonces, la resistividad aparente ρa = 1+ 4πaR − √ 2a a2 +4b2 ρa es (1.2.2) √ a a2 +b2 b es pequeño en comparación con a, ya que se colocan cuatro picas a, accionadas a una profundidad no superior a 0,1a. Entonces, se En la práctica, generalmente en una línea recta a intervalos puede asumir que b=0 y la ecuación (1.2.2) se reduce a ρa = 2πaR Con lo que se tiene la resistividad aparente aproximada del terreno a la profundidad (1.2.3) a. Las lecturas obtenidas con diferentes distancias entre las sondas se pueden gracar usando la resistividad contra la separación como se muestra en la Figura 1.2.2. De esta manera se puede estimar si existen diferentes capas del terreno y se tiene una idea de sus respectivas resistividades y profundidades. Figura 1.2.2: Curva de resistividad típica [6]. Espaciamiento desigual o Schlumberger Un inconveniente del método Wenner es el requisito de reposicionar las cuatro picas para cada profundidad a medir. La disposición mostrada en la Figura 1.2.3 (b) puede usarse para medir 5 con éxito la resistividad del terreno cuando las picas de corriente están separadas por una gran distancia o para acelerar la prueba para múltiples localizaciones de la pica de corriente. Con el método de Schlumberger, las picas interiores se colocan más juntas y las picas exteriores se colocan más separadas. A diferencia del método de Wenner, que requiere que todas las picas se muevan para calcular la resistividad del terreno a diferentes profundidades, el método de Schlumberger solamente requiere que las picas externas sean reposicionadas para nuevas mediciones. Reducir el número de picas a reposicionar para cada prueba hace que el método Schlumberger sea una opción más rápida para pruebas a diferentes profundidades. Si la profundidad de enterramiento de las picas c, y c>2d, b es pequeña comparada con su separación d y entonces la resistividad aparente medida se puede calcular como sigue ρa = πc(c + d)R d (1.2.4) La resistividad calculada por la ecuación (1.2.4) es la resistividad aparente a la profundidad 2c+d 2 , que es la distancia desde el centro de la prueba a las picas de corriente externas de la Figura 1.2.3 (b). aproximada Figura 1.2.3: Método de cuatro puntos: (a) picas equidistantes y (b) picas espaciadas de manera desigual [6]. Es recomendable realizar las mediciones a lo largo de varios perles alrededor del área de análisis para detectar posibles cambios laterales en la resistividad del terreno, así como para determinar cualquier posible efecto de interferencia en las mediciones debidas a objetos conductores cercanos. Otra manera de ganar la conanza de que los objetos conductores en la tierra no afecten a las mediciones es repetir la medición en la misma ubicación, pero a valores medidos deben correlacionarse. 6 90º con respecto a la primera. Los 1.2.2. Interpretación de las mediciones La interpretación de los valores medidos de las resistividades es tal vez la parte más difícil del análisis. Debido a que la variación de la resistividad del terreno puede ser grande y compleja por la heterogeneidad de la misma. El modelo del terreno es sólo una aproximación de las condiciones reales del terreno y es improbable una combinación perfecta. Los modelos de resistividad del terreno más utilizados son el modelo de terreno uniforme y el modelo de terreno de dos capas. En algunos casos, la variación en la resistividad del terreno puede presentar mínimos y máximos tales que un modelo equivalente de dos capas puede no producir un modelo preciso. En tales casos puede ser necesario un modelo de terreno diferente, tal como un modelo 2 multicapa mediante el uso de programas informáticos. A veces, en un terreno multicapa, la variación en la resistividad aparente del terreno ρa con respecto a la profundidad o el espaciamiento entre picas no es demasiado grande. Este terreno puede representarse como uniforme con un solo valor de resistividad. 1.2.3. Modelo de terreno uniforme Se puede usar este modelo cuando existe una variación moderada en la resistividad aparente del terreno teniendo un resultado razonablemente preciso. Por otro lado, si se tiene una variación signicativa en las mediciones de la resistividad aparente, es difícil desarrollar un modelo de terreno uniforme que produzca resultados precisos. La resistividad uniforme aproximada del terreno se puede obtener tomando una media aritmética de los datos de la resistividad aparente medida como se muestra en la ecuación (1.2.5). ρa(av1) = ρa(1) + ρa(2) + ρa(3) + ... + ρa(n) n (1.2.5) Donde ρa(1), ρa(2), ρa(2)...ρa(n) n son los datos medidos de resistividad aparente [Ω · m] el número total de mediciones 1.2.4. Modelo de terreno de dos capas por el método gráco Se puede obtener una representación más exacta de las condiciones reales del terreno mediante el uso de un modelo de dos capas. El modelo de dos capas consiste en una capa superior de profundidad nita y con diferente resistividad que una capa inferior de espesor innito. Existen varias técnicas para determinar un modelo de terreno de dos capas aproximado a partir de la resistividad aparente obtenida de las pruebas de campo. Una manera es usando el método gráco (Sunde) que se muestra en la Figura 1.2.4, la cual se basa en los datos obtenidos mediante el método de cuatro puntos arreglo Wenner para la medición de la resistividad. A continuación, se detallan los pasos a seguir para determinar la profundidad de la capa supercial h mediante el método gráco Sunde. Las resistividades de la capa supercial más profunda ρ2 espaciamiento de las picas de prueba. 2 Más ρ1 y de la capa son determinadas por inspección visual de la gráca de resistividad aparente vs de dos capas horizontales. 7 a) Dibujar una curva de resistividad aparente vs espaciamiento de las picas de prueba de los datos que se obtienen en las mediciones. b) Estimar, de la curva trazada en a), la resistividad que corresponde a una separación menor y la resistividad de una mayor separación c) ρ1 ρ2 . ρ2 ρ1 y seleccionar la curva de la gráca Sunde en la Figura 1.2.4, si no se tiene una curva exacta se puede seleccionar la curva más cercana o interpolar y dibujar una nueva Determinar curva en el gráco. Figura 1.2.4: Gráca de Sunde [8]. d) Seleccionar el valor de ρa ρ2 ρ1 en el eje Y, dentro de la región de la pendiente de la curva ρ1 encontrada en c). e) Leer el valor que corresponde a f) Multiplicar el valor de g) Leer la separación de las picas ρa ρ1 por a h en el eje X. ρ1 , a para obtener ρa . en la curva de resistividad aparente trazada en a), con se obtuvo en f ). h) Calcular h , mediante la multiplicación de a h por 8 a. ρa que 1.3. Diseño del sistema de puesta a tierra Para el diseño eciente de un sistema de puesta a tierra, es importante tener el conocimiento de los parámetros que afectan su rendimiento, tales como el espaciamiento y la disposición de los conductores de la malla, el número de varillas de tierra, la ubicación y la longitud, entre otros. Un sistema de puesta a tierra normalmente incluye conductores de cobre desnudo que pueden estar enterrados entre 0,3m y 0,5m por debajo del nivel de la supercie, con un espaciamiento entre 3m a 7m. En las conexiones de cruce, los conductores deben estar unidos jamente entre sí. En cuanto a las varillas de tierra se pueden colocar en las esquinas de la malla y en los puntos de unión a lo largo del perímetro [8]. La implementación de múltiples varillas estrechamente espaciados no reducirán la resistencia de puesta a tierra. Debido a la resistencia mutua común en la que la corriente de cada uno eleva el voltaje del otro. Dado que la tensión es mayor para el mismo ujo de corriente, la resistencia se incrementa por la resistencia mutua. Cuando se utilizan múltiples varillas, los espaciamientos de menos de 3m pueden no proporcionar el uso más económico de los materiales. Pruebas realizadas por el Instituto Nacional de Ciencia y Tecnología (NIST, por sus siglas en inglés) muestran que la resistencia disminuye sólo alrededor del 5 % cuando la profundidad de entierro aumenta de 0,5m a 1m, en base a una resistividad uniforme del terreno. Del mismo modo, el efecto del tamaño del conductor es extremadamente pequeño [8]. En el diagrama de bloques mostrado en la Figura C.3 (ANEXO C) se ilustra las secuencias de pasos recomendados según el estándar IEEE 80-2013 para el diseño de una malla de tierra, a continuación se detallan los principales pasos. 1.3.1. Paso 1: Área de estudio El estudio de la 3 resistividad del terreno, descrito en el apartado 1.2, determinará el perl de la resistividad y el modelo del terreno necesario. 1.3.2. Paso 2: Conductor La selección apropiada del material conductor mantendrá la integridad de un sistema de puesta a tierra durante años si los conductores son de tamaño adecuado y las condiciones del terreno no son corrosivas para el material utilizado. Los materiales comúnmente usados para el conductor de un sistema de puesta a tierra se describen a continuación. Cobre El cobre es el material más utilizado en los sistemas de puesta a tierra. Los conductores de cobre tienen una alta 4 conductividad, además tienen la ventaja de ser resistentes a la corrosión subterránea ya que el cobre es catódico con respecto a la mayoría de los otros metales que pueden estar enterrados en los alrededores. Acero con revestimiento de cobre El acero revestido de cobre es un material utilizado para sistemas de puesta a tierra, especialmente donde el robo del conductor puede ser un problema. 3 Es la propiedad del terreno que se opone al paso de la 4 Poder conductivo de un material, es la acción opuesta 9 corriente eléctrica. a la resistividad. Aluminio Este material se usa raramente para las mallas de tierra, debido a que presenta las siguientes desventajas: a) El propio aluminio puede corroerse en ciertos terrenos. No se recomienda utilizar el conductor de aluminio bajo tierra. b) La corrosión gradual causada por corrientes alternas también puede ser un problema bajo ciertas condiciones. El aluminio es anódico a muchos otros metales, incluyendo el acero. Acero Pueden usarse conductores de acero o acero inoxidable y varillas de tierra en aplicaciones donde las condiciones del terreno pueden ser perjudiciales para el cobre. El uso de acero revestido de zinc o acero inoxidable, en combinación con protección catódica, es típico para sistemas de puesta a tierra de acero [8]. 1.3.2.1. Cálculo del calibre del conductor La sección transversal del conductor se determina mediante la ecuación (1.3.1), en donde la corriente de falla debe ser la máxima corriente futura de falla esperada que puede ser conducida por cualquier conductor del sistema de tierra, y el tiempo tc , debe reejar el tiempo de despeje máximo posible. Amm2 = q IF (1.3.1) ·10−4 0 +Tm )ln( K ( T CAP tc αr ρr K0 +Ta ) Donde IF es la máxima corriente de falla asimétrica Amm2 Tm es la sección transversal del conductor [kA] [mm2 ] es la temperatura máxima permisible de fusión [◦ C] Ta es la temperatura ambiente [°C] Tr es la temperatura de referencia de constantes de materiales [°C] α0 es el coeciente térmico de resistividad a 0 °C αr es el coeciente térmico de resistividad a la temperatura de referencia ρr es la resistividad del conductor de tierra a la temperatura de referencia K0 tc es 1/α0 o [1/°C] Tr [1/°C] Tr [µΩ · cm] (1/α0 ) − Tr [°C] es la duración de la corriente de falla[s] T CAP es el factor [J/(cm3 · °C)] de capacidad térmica por unidad de volumen obtenido de la Tabla 1.3.2.1 Debe observarse que αr y ρr se encuentran a la misma temperatura de referencia 1.3.2.1 proporciona los datos de αr y ρr a una temperatura de referencia de 10 20°C . Tr . La Tabla Descripción Conductividad del material Factor αr a 20°C ( %) (1/°C ) 100.0 0.00393 97.0 K0 a 0 ◦ C (◦ C ) Temperatura de fusión Tm ◦ ρr a 20 ◦ C Capacidad térmica T CAP ( C) (µΩ · cm) 234 1083 1.72 3.4 0.00381 242 1084 1.78 3.4 40.0 0.00378 245 1084 4.40 3.8 30.0 0.00378 245 1084 5.86 3.8 17.0 0.00378 245 1084 10.1 3.8 20.3 0.00360 258 657 8.48 3.561 10.8 0.00377 245 1510 15.90 3.8 9.8 0.00377 245 1400 17.50 4.4 8.6 0.00320 293 419 20.10 3.9 2.4 0.00130 749 1400 72.00 4.0 [J/(cm3 · °C)] Cobre destemplado trenzado suave Cobre comercial trenzado duro Alambre de acero con revestimiento de cobre Alambre de acero con revestimiento de cobre Varilla de acero con revestimiento de cobre Alambre de acero con revestimiento de aluminio Acero, 1020 Varilla de acero con revestimiento inoxidable Varilla de acero con capa de zinc Acero inoxidable 304 Tabla 1.1: Constantes de materiales [8]. El tamaño del conductor realmente seleccionado por lo general es mayor que el basado en la fusión debido a factores tales como: a) El conductor debe tener la resistencia necesaria para soportar cualquier abuso mecánico y corrosivo durante la vida de diseño de la instalación de puesta a tierra. b) El conductor debe tener una conductividad lo sucientemente alta como para evitar cualquier posible caída de tensión peligrosa durante una falla, durante la vida útil de la instalación de puesta a tierra. c) La necesidad de limitar la temperatura del conductor. d) Se debe aplicar un factor de seguridad al sistema de puesta a tierra al igual que con otros componentes eléctricos. 1.3.3. Paso 3: Tensiones tolerables Los valores de las tensiones tolerables de paso y de contacto para un ser humano sometido a peligro, con pesos corporales de 50kg y 70kg se determinan por las ecuaciones (1.3.2), (1.3.3), (1.3.4) y (1.3.5): Tensión de paso para una persona con peso corporal de 50 kg y 70kg 0,116 Epaso50kg = (1000 + 6Cs × ρs ) √ ts 11 (1.3.2) 0,157 Epaso70kg = (1000 + 6Cs × ρs ) √ ts (1.3.3) Tensión de contacto para una persona con peso corporal de 50 kg y 70kg 0,116 Econtacto50kg = (1000 + 1,5Cs × ρs ) √ ts (1.3.4) 0,157 Econtacto70kg = (1000 + 1,5Cs × ρs ) √ ts (1.3.5) Donde Epaso es la tensión de paso Econtacto [V ] es la tensión de contacto [V ] Cs es calculada por la ecuación (1.3.6) ρs es la resistividad de la capa supercial del terreno ts es el tiempo de despeje de la falla [Ω · m] [s] ts , se basa en el juicio del ingeniero de diseño. Normalmente se supone que tf y la duración del choque ts son iguales, a no ser que la duración de la los choques sucesivos, como los de los cierres. Los valores típicos para tf y ts La elección del tiempo la duración de la falla falla sea la suma de varían de 0.25s a 1s. El factor Cs depende del espesor y resistividad del material supercial, así como de la resisti- vidad del terreno, y se calcula mediante la ecuación (1.3.6). Cs = 1 − 0,09(1 − ρ ρs ) (1.3.6) 2hs + 0,09 Donde Cs es el factor de decremento de la capa supercial hs es el espesor de la capa supercial ρ es la resistividad del terreno [m] [Ω · m] Cuando no se tiene prevista una capa supercial (grava), entonces Cs = 1 y ρs = ρ. La capa de material supercial normalmente es de 0.10m a 0.15m de material de alta resistividad, como grava, usualmente se extiende sobre la supercie por encima de la malla de tierra para aumentar la resistencia de contacto entre el terreno y los pies de las personas La corriente a través del cuerpo se reducirá considerablemente con la adición del material supercial debido a la mayor resistencia de contacto entre la tierra y los pies. 1.3.4. Paso 4: Diseño Básico El diseño preliminar debe incluir un conductor perimetral que rodee el área de puesta a tierra, formado por conductores para proporcionar un acceso conveniente a los conductores de puesta a tierra de los equipos y estructuras. Las estimaciones iniciales de la separación de los conductores, así como la ubicación de las varillas de tierra, se deben basar en la corriente IG 12 y el área del terreno que será puesto a tierra. 1.3.5. Paso 5: Resistencia a tierra 1.3.5.1. Ecuación general El valor preliminar de la resistencia de puesta a tierra de una malla en un terreno uniforme es determinado mediante la ecuación (1.3.7). Rg = ρ[ 1 1 1 p +√ (1 + )] LT 20A 1 + h 20/A (1.3.7) Donde Rg ρ es la resistencia del sistema de puesta a tierra es la resistividad del terreno LT [Ω] [Ω · m] es la longitud total de los conductores enterrados (conductores horizontales + varillas verticales) [m] h es la profundidad de la malla de tierra A es el área de la malla de tierra [m] [m2 ] Para las mallas sin varillas de tierra, esta fórmula ha sido probada para obtener resultados prácticamente idénticos a los obtenidos con la ecuación (1.3.8) de Schwarz, descrita a continuación. 1.3.5.2. Ecuaciones de Schwarz Schwarz desarrolló una serie de ecuaciones para determinar la resistencia total de un sistema de puesta a tierra en un terreno homogéneo formado por electrodos en disposición horizontal (conductor) y verticales (varillas). Las ecuaciones ampliadas de Schwarz presentan a un conductor recto horizontal que representa la 5 R1 , de una malla que consiste en conductores enR2 . También presentó mutua, Rm entre la malla y las varillas. resistencia de tierra, trelazados, y una esfera inscrustada en la tierra para representar las varillas una ecuación para la resistencia de tierra Schwarz utiliza la ecuación (1.3.8) introducida por Sunde y Rüdenberg para combinar la resistencia de la malla, las varillas y la resistencia a tierra mutua, para calcular la resistencia total del sistema, Rg . Rg = 2 R1 R2 − Rm R1 + R2 − 2Rm (1.3.8) Donde R1 es la resistencia a tierra de los conductores de la malla R2 es la resistencia a tierra de todas las varillas de tierra Rm [Ω] [Ω] R1 , es la resistencia mutua entre el grupo de conductores de la malla, de tierra, y un grupo de varillas R2 , [Ω] La resistencia a tierra de los conductores de la malla R1 = R1 , se calcula mediante la ecuación (1.3.9). 2Lc k1 × Lc ρ [ln( )+ √ − k2 ] πLc a´ A (1.3.9) Donde ρ es la resistividad del terreno Lc a´ [Ω · m] es la longitud total de todos los conductores conectados a la malla √ es 5 Es a · 2h es para conductores enterrados a una profundidad h [m] [m], ó la resistencia que ofrece el terreno hacia la corriente en un sistema de puesta a tierra. 13 a´ es 2a es el diámetro del conductor A a para el conductor en la supercie de la tierra [m] es el área cubierta por los conductores k1 , k2 [m] [m2 ] son los coecientes [véase la Figura 1.3.1 (a) y (b)] La resistencia a tierra de las varillas R2 , se calcula usando la ecuación (1.3.10). ρ 4Lr 2k1 · Lr √ [ln( )−1+ √ ( nR − 1)2 ] 2πnR Lr b A R2 = (1.3.10) Donde Lr es la longitud de cada varilla 2b es el diámetro de la varilla nR [m] [m] es el número de varillas situado en la zona A La resistencia a tierra mutua entre la malla y las varillas Rm , se calcula por medio de la ecuación (1.3.11). Rm = ρ 2Lc k1 × Lc − k2 + 1] [ln( )+ √ πLc Lr A (1.3.11) La ecuación (1.3.11) también puede reescribirse como la ecuación (1.3.12). Rm = R1 − Figura 1.3.1: Coecientes k1 y k2 ρ Lr ) − 1] [ln( √ πLc h × 2a de la fórmula de Schwarz: (a) coeciente [8]. 14 (1.3.12) k1 , (b) coeciente k2 1.3.5.3. Ecuacion de Dwight Un sistema de puesta a tierra de baja resistencia, es de gran importancia para satisfacer los requisitos de los alimentadores de sistemas de las empresas de servicios públicos, donde el camino de retorno de falla es a través del terreno. Cuanto menor sea la resistencia del sistema de puesta a tierra, más adecuadamente se cumplen estos requisitos. Sin embargo, las instalaciones con menores niveles disponibles de corriente de falla a tierra no requieren un valor tan bajo de resistencia como los sistemas más grandes con niveles más altos de corriente [3]. Las resistencias de tierra de los sistemas inferiores a 1 ohm se pueden obtener mediante el uso de un número de electrodos individuales conectados entre sí. Esta baja resistencia sólo es necesaria para grandes subestaciones, líneas de transmisión o estaciones generadoras. Las resistencias en el rango de 1 ohm a 5 ohm se encuentran generalmente adecuadas para subestaciones de plantas industriales, edicios y grandes instalaciones comerciales [3]. El valor de 25 ohmios indicado en el NEC, se aplica a la resistencia máxima para un solo electrodo que consiste en una barra, tubería o placa. Esto no debe interpretarse en el sentido de que 25 ohmios sea un valor de resistencia satisfactorio para un sistema de puesta a tierra [9]. El cálculo ha sido simplicado en gran medida por las fórmulas desarrolladas en Dwight y presentadas en la Tabla C.1 (ANEXO C ). Debe indicarse que estas fórmulas son sólo aproximaciones y dado el estado de las capacidades de hoy en día con respecto a los modelos derivados de computadora de sistemas de tierra, se debe considerar el uso de esas herramientas. Múltiples varillas en paralelo producen una menor resistencia a tierra que una sola varilla. Las varillas múltiples se utilizan comúnmente para proporcionar la baja resistencia a tierra requerida por instalaciones de alta capacidad. La adición de una segunda varilla no proporciona, sin embargo, una resistencia total de la mitad de una sola varilla, a menos que las dos varillas tengan distintas longitudes [3]. En el desarrollo de este proyecto realiza la comparación entre en valor calculado y medido de una varilla. Siendo así, que la resistencia de contacto de una varilla visto en la Tabla C.1 (ANEXO C) está dada por la fórmula de Dwight: R= 4L ρ (ln − 1) 2πL a (1.3.13) Donde ρ es la resistividad del terreno L es la longitud de la varilla a es el radio de la varilla 1.3.5.4. [Ω · m] [m] [m] Ecuaciones adicionales En este apartado se determinan las ecuaciones para calcular la resistencia del sistema de puesta a tierra de las conguraciones mostradas en la Figura 1.3.2 15 Figura 1.3.2: Conguraciones de puesta a tierra: (a) unión de dos varillas, (b) unión de tres varillas y (c) unión de tres varillas en forma triangular. Cálculo de la resistencia de la unión de dos y tres varillas en disposición lineal El cálculo de la resistencia de puesta a tierra para las conguraciones de dos y tres varillas en disposición lineal que se muestran en la Figura 1.3.2 (a) y (b) respectivamente, se determina mediante la modicación de las Ecuaciones de Schwarz de la siguiente manera: En primera instancia, las ecuaciones de Schwarz involucran un área, mientras que las disposiciones de las varillas analizadas en este apartado no cuentan con este parámetro. Debido a ello, se realiza una hipótesis tomando la longitud total del conductor cuadrado, entonces para las constantes de inuencia es de ( L4C )2 . k1 y k2 (Lc ) como el perímetro de un x = 1 y el valor del área R1 de la ecuación (1.3.9) de la Figura 1.3.1 el valor Entonces, la resistencia a tierra del conductor se reescribe de la siguiente manera R1 = ρ 2Lc ) + 4k1 − k2 ] [ln( πLc a´ Mientras que la resistencia a tierra de las varillas R2 = R2 (1.3.14) de la ecuación (1.3.10) se reescribe como: ρ 8k1 × Lr √ 4Lr )−1+ [ln( ( nR − 1)2 ] 2πnR Lr b Lc Donde R1 es la resistencia a tierra del conductor [Ω] R2 es la resistencia a tierra de las varillas [Ω] ρ es la resistividad del terreno Lc es la longitud del conductor √ a´ es a´ es a b a a · 2h para el conductor en la supercie del terreno [m] es la longitud de cada varilla es el radio de la varilla nR [m] es para el conductor enterrado a una profundidad es el radio del conductor Lr [Ω · m] [m] [m] es el número de varillas 16 [m] h [m], o (1.3.15) Ecuaciones para dos varillas Para dos varillas se tiene que reemplazar por d, nR = 2, y según la Figura 1.3.2 (a) el valor de Lc se puede de esta manera las ecuaciones (1.3.12), (1.3.14) y (1.3.15) se reescriben como: 2d ρ [ln( ) + 4k1 − k2 ] πd a´ (1.3.16) ρ 4Lr 8k1 × Lr √ [ln( )−1+ ( 2 − 1)2 ] 4πLr b d (1.3.17) R1 = R2 = Rm = R1 − ρ Lr ) − 1] [ln( √ πd h × 2a (1.3.18) Donde d es la distancia de separación entre las dos varillas Una vez calculado Rm , d > Lr , [m] se procede a calcular la resistencia total del sistema (Rg ) usando la ecuación (1.3.8) de Schwarz. Ecuaciones para tres varillas en disposición lineal Para tres varillas se tiene que nR = 3, y según la Figura 1.3.2 (b) el valor de Lc = 2d, de esta manera las ecuaciones (1.3.12), (1.3.14) y (1.3.15) se reescriben como: 4d ρ [ln( ) + 4k1 − k2 ] 2πd a´ (1.3.19) 4Lr 4k1 × Lr √ ρ [ln( )−1+ ( 3 − 1)2 ] 6πLr b d (1.3.20) R1 = R2 = Rm = R1 − ρ Lr [ln( √ ) − 1] 2πd h × 2a (1.3.21) Donde d es la distancia de separación entre dos varillas adyacentes Una vez calculado Rm , d > Lr , [m] se calcular la resistencia total del sistema (Rg ) usando la ecuación (1.3.8) de Schwarz. Ecuaciones para tres varillas en disposición triangular Para calcular la resistencia de tierra de una malla formada por un triángulo ilustrado en la Figura 1.3.2 (c) se asume x=1 para el cálculo de las constantes k1 y k2 , considerando que x es igual a uno siempre y cuando el largo y el ancho de una malla sean iguales, así mismo el triángulo equilátero no pierde su forma con cualquier valor de longitud de sus lados, por lo que se realiza una 6 analogía entre estos parámetros. Además, se conoce que nR = 3 y Lc = 3d; por lo tanto, las ecuaciones (1.3.9), (1.3.10) y (1.3.12) se reescriben como: ρ 6d 3k1 × d [ln( ) + √ − k2 ] 3πd a´ A (1.3.22) ρ 4Lr 2k1 · Lr √ [ln( )−1+ √ ( 3 − 1)2 ] 6πLr b A (1.3.23) R1 = R2 = Rm = R1 − ρ Lr [ln( √ ) − 1] 3πd h × 2a (1.3.24) Donde d es la distancia de separación de cada lado del triángulo Una vez calculado Rm , (1.3.8) de Schwarz. 6 Relación d > Lr , [m] se calcular la resistencia total del sistema (Rg ) usando la ecuación de semejanza entre cosas distintas. 17 1.3.6. Paso 6: Corriente máxima de malla IG . La corriente máxima de malla IG , que puede propagarse en una malla de tierra en casos de falla, está determinada mediante la ecuación (1.3.25). Para evitar sobre dimensionar el sistema de puesta a tierra, solamente se debe usar la parte de la corriente de falla que uye a través de la malla de tierra y hacia el terreno contiguo. IG = Df × Ig = Df × Sf × If (1.3.25) Donde IG Ig Df es la corriente máxima de malla [A] es el valor ecaz de la corriente simétrica en la malla es el factor de disminución para toda la duración tf [A] de la falla Sf es el factor de división de corriente de falla If es el valor ecaz de la corriente de falla simétrica a tierra Df El factor de decremento, [A] es usado para incluir el efecto de la componente DC. Este factor determina el equivalente rms (valor ecaz) de la onda de corriente asimétrica para una duración de falla determinada, tf , teniendo en cuenta el efecto de la componente DC inicial y su atenuación durante la falla [16]. En la Tabla 1.2 se pueden observar los valores de Duración de falla, Segundos tf Ciclos a 60 Df . X/R = 10 X/R = 20 Df X/R = 30 X/R = 40 Factor de decremento, Hz 0.00833 0.5 1.576 1.648 1.675 1.688 0.05 3 1.232 1.378 1.462 1.515 0.10 6 1.125 1.232 1.316 1.378 0.20 12 1.064 1.125 1.181 1.232 0.30 18 1.043 1.085 1.125 1.163 0.40 24 1.033 1.064 1.095 1.125 0.50 30 1.026 1.052 1.077 1.101 0.75 45 1.018 1.035 1.052 1.068 1.00 60 1.013 1.026 1.039 1.052 Tabla 1.2: Valores típicos de Df [8]. 1.3.7. Paso 7: Potencial Máximo de la Malla (GP R). La elevación de potencial de tierra, GP R, se determina mediante la ecuación (1.3.26). GP R = IG · Rg (1.3.26) Donde IG es la corriente máxima de malla Rg es la resistencia de la malla [A] [Ω] Si el valor de la máxima elevación del potencial de tierra del diseño preliminar está por debajo de la tensión de toque tolerable por el cuerpo humano, ya no es necesario realizar análisis adicionales. Y se procede a poner a tierra los equipos. 18 1.3.8. Paso 8: Tensión de paso y de contacto reales Para el cálculo de la tensión de paso real se utiliza la ecuación (1.3.27) Es = ρ × Ks × Ki × IG Ls (1.3.27) Donde Es ρ es la tensión de paso [V ] es la resistividad del terreno [Ω · m] Ks es el factor de espaciamiento para la tensión de paso Ki es el factor de corrección para la geometría de la malla IG es la corriente máxima de la malla Ls es la longitud efectiva del conductor para la tensión de paso [A] [m] Para mallas con o sin varillas de aterrizaje, la longitud enterrada efectiva, Ls , se calcula mediante la ecuación (1.3.28). Ls = 0,75 × LC + 0,85 × LR (1.3.28) Donde LC es la longitud total del conductor de la malla LR es la longitud total de todas las varillas de aterrizaje El factor de espaciamiento para la tensión de paso, Ks = [m] [m] Ks , se calcula por medio de la ecuación (1.3.29). 1 1 1 1 [ + + (1 − 0,5n−2 )] π 2×h D+h D (1.3.29) Donde h D n [m] es la profundidad a la que se encuentra enterrada la malla es el espaciamiento entre conductores paralelos [m] es el número efectivo de conductores paralelos en una malla El factor de corrección para la geometría de la malla, Ki , se calcula por medio de la ecuación (1.3.30). Ki = 0,644 + 0,148 × n (1.3.30) El cálculo de la tensión de contacto real se determina mediante la ecuación (1.3.31). Em = ρ × Km × Ki × IG LM (1.3.31) Donde Em es la tensión de contacto [V ] Km es el factor de espaciamiento para la tensión de contacto LM es la longitud efectiva del conductor de la malla para la tensión de contacto El factor de espaciamiento para la tensión de contacto, Km = Km , [m] se calcula de la siguiente manera: 1 D2 (D + 2 × h)2 h Kii 8 × [ln( + − )+ × ln( )] 2×π 16 × h × d 8×D×d 4×d Kh π(2 × n − 1) Donde 19 (1.3.32) d es el diámetro del conductor de la malla [m] Kii es el factor de ponderación correctivo que se ajusta para efectos de conductores internos Kh es el factor de ponderación correctivo que hace hincapié en los efectos de la profundidad de la malla El factor de ponderación correctivo, Kii , para mallas con varillas de aterrizaje a lo largo de su perímetro, o para mallas con varillas de aterrizaje en sus esquinas o dentro de la misma es: Kii = 1 Mientras que para mallas sin varillas de aterrizaje o mallas con pocas varillas de aterrizaje, ninguna de ellas colocadas en las esquinas o en el perímetro se tiene que: Kii = El valor de Kh 1 es: r Kh = Donde, (1.3.33) 2 (2 × n) n h0 = 1m 1+ h h0 (1.3.34) (profundidad de referencia de la malla) El número efectivo de conductores paralelos en una malla n es: n = na × nb × nc × nd (1.3.35) Donde na = 2 × LC Lp (1.3.36) nb = 1 Para mallas cuadradas nc = 1 Para mallas cuadradas y para mallas rectangulares nd = 1 Para mallas cuadradas, para mallas rectangulares y para mallas en forma de L De otra manera: s nb = nc = [ Lp √ 4× A (1.3.37) Lx × Ly L0,7×A ] x ×Ly A nd = q (1.3.38) Dm (1.3.39) L2x + L2y Donde LC Lp A es la longitud total del conductor de la malla es la longitud perimetral de la malla es el área de la malla [m] [m] [m2 ] Lx es la longitud máxima de los conductores de malla en dirección de x [m] Ly es la longitud máxima de los conductores de malla en dirección de y [m] Dm es la distancia máxima entre dos puntos cualesquiera de la malla 20 [m] Para mallas sin varillas de aterrizaje o mallas con tan solo algunas varillas dispersas a los largo de la malla, pero colocada en las esquinas o sobre todo en el perímetro de la malla, la longitud efectiva del conductor de la malla para la tensión de contacto, LM , es: LM = LC + LR (1.3.40) Donde LC es la longitud total del conductor de la malla [m] LR es la longitud total de todas las varillas de aterrizaje [m] Para mallas con varillas de aterrizaje en las esquinas, así como a los largo de su perímetro y sobre toda la malla, la longitud efectiva del conductor de la malla para la tensión de contacto, Lr )]LR LM = LC + [1,55 + 1,22( q 2 Lx + L2y Lr es la longitud de cada varilla de aterrizaje LM , es: (1.3.41) [m] 1.3.9. Paso 9 y Paso 10: Control de seguridad Si las tensiones de paso y de contacto calculadas están por debajo de las tensiones de paso y de contacto tolerables por el cuerpo humano, el diseño sólo necesita la puesta a tierra de los equipos (ver paso 12). De lo contrario, el diseño preliminar debe ser revisado (ver paso 11). 1.3.10. Paso 11: Acciones de Mejora Si se superan los límites tolerables de las tensiones de paso o de contacto, se requiere una revisión del diseño de la malla. Esta revisión puede incluir la reducción del espaciamiento entre conductores, el incremento de electrodos de tierra, el aumento del área ocupada por la malla, etc. Además, se puede considerar el uso de un material de supercie con una resistividad mayor o el aumento del espesor del material de la capa supercial, para incrementar las tensiones tolerables del cuerpo humano. 1.3.11. Paso 12: Poner a tierra todos los equipos Después de satisfacer los requisitos de tensiones de paso y toque, se debe incluir los conductores requeridos para poner a tierra los equipos a la malla. Hay que tener en cuenta que pueden requerirse conductores y varillas de tierra adicionales cerca de los equipos como descargadores de sobretensión, neutro de transformadores, entre otros [10]. 1.4. Tratamiento del terreno De acuerdo a Jinliang He[14], en la actualidad, el método común para reducir la resistencia de puesta a tierra consiste en mejorar la conductividad del terreno mediante un tratamiento químico. Con este tratamiento del terreno reduce su resistividad añadiendo Material de Baja Resistividad (LRM, por sus siglas en inglés) alrededor de un electrodo vertical en el oricio perforado o en una zanja de tierra para conductores horizontales, con el propósito de mejorar la conductividad eléctrica del terreno y así reducir la resistencia de puesta a tierra. Una manera ecaz de reducir la resistencia de puesta a tierra es aumentar el tamaño del electrodo, por lo que la disminución de la resistividad del terreno alrededor del electrodo es en cierto grado equivalente a aumentar el tamaño del mismo. LRM es un tipo de polvo con partículas nas. Por lo tanto, su contacto con el electrodo y el terreno puede considerarse como un contacto supercial perfecto. El área de contacto entre el electrodo de tierra y el terreno se incrementa y la resistencia de contacto entre el electrodo y la tierra se reduce, por otro lado, reduce la resistencia a la dispersión de corriente. 21 Las fórmulas para calcular las resistencias de puesta a tierra se basan todas en el contacto perfecto entre el terreno y el electrodo de tierra. La fórmula para calcular la resistencia de puesta a tierra de una varilla cubierto con LRM, como se muestra en la Figura 1.4, se presenta en la ecuación (1.4.1). 4l ρ1 d1 ρ ln + ln 2πl d1 2πl d R= (1.4.1) Donde R ρ es la resistividad del terreno ρ1 l [Ω] es la resistencia de puesta a tierra [Ω · m] es la resistividad del área con LRM es la longitud del electrodo vertical d es el diámetro del electrodo d1 [Ω · m] [m] [m] es el diámetro del área con LRM [m] Figura 1.4.1: Electrodo vertical cubierto con LRM [14]. Debido a que dl, d1 l, ρ1 ρ, el diámetro de la varilla de tierra vertical aumenta a d1 , entonces la ecuación (1.4.1) puede reescribirse como: R= ρ 4l ln 2πl d1 (1.4.2) Para un electrodo o conductor en disposición horizontal con profundidad de entierro h, como se muestra en la Figura 1.4, la resistencia de puesta a tierra cubierta LRM se presenta en la ecuación (1.4.3). R= ρ l2 ρ1 d 1 ln + ln 2πl d1 h 2πl d (1.4.3) Donde d1 l es el diámetro equivalente del área con LRM es la longitud del electrodo horizontal [m] [m] Dado que el diámetro del electrodo de tierra aumenta a d1 cuando ρ1 ρ, la ecuación (1.4.3) se puede reescribir como: R= ρ l2 ln 2πl d1 h 22 (1.4.4) Figura 1.4.2: Electrodo de tierra horizontal cubierto con LRM [14]. El uso de LRM para la disminución de la resistencia de puesta a tierra puede usarse independientemente de si el electrodo de tierra es hemisferio, vertical u horizontal. 1.4.1. Ingredientes de LRM El LRM está compuesto por un agente líder junto con un agente adhesivo, un agente aditivo, un electrolito, un agente solidicante y agua. Generalmente, el agente principal puro tiene una alta resistividad, pero después de añadir electrolito y agua, se convierte en un LRM con una resistividad muy baja. Cuanto menor sea está resistividad, mejor será el efecto en la disminución de resistencia de puesta a tierra. El estándar IEEE 80-2013 recomienda utilizar diversos métodos ecaces para reducir la resistividad del terreno en el sistema de puesta a tierra, tal como bentonita, electrodo del tipo químico y material del refuerzo del terreno. 1.4.2. Requisitos básicos para LRM Los requisitos básicos para LRMs incluyen: a) Seguro para animales y plantas b) Buena conductividad c) Baja corrosividad d) Estabilidad a largo plazo e) Fácil de usar en la instalación Los resultados de las pruebas muestran que la velocidad de corrosión del acero de bajo contenido de carbono recubierto con LRM en un terreno altamente corrosivo es mucho menor que sin estar cubierto con LRM, lo que indica que el LRM puede reducir la corrosión de un electrodo de tierra y extender su vida útil. 1.4.3. Conductividad de LRM Una buena conductividad eléctrica es un rendimiento básico pero necesario para un LRM. Debe tener una resistividad mucho menor que el terreno. Para mantener este rendimiento, debe contener un componente llamado agente líder para mantener el agua. El terreno rojo arenoso y la se han utilizado durante mucho tiempo como agentes principales. 7 Es una arcilla de grano muy no dilatándose con la exposición al agua 23 7 bentonita Los dispositivos de tierra de protección contra rayos recubiertos con un LRM sufrirán corrientes de decenas de kilo-amperios, a veces incluso cientos de kilo-amperios. El LRM debe cumplir con el requisito de una corriente de impulso. La resistividad de LRM puede mantenerse básicamente sin cambios después de soportar 20 ataques de una corriente de impulso con magnitud de 10 kA y una forma de onda de 8/20µs. Por lo tanto, tiene un efecto perfecto en la dispersión de corrientes de impulso. Así mismo, cuando se produce un accidente de cortocircuito, la corriente de frecuencia de potencia puede alcanzar decenas de kilo-amperios. Las pruebas muestran que la resistividad disminuye aproximadamente 12 % después de que el LRM soporta cinco impactos de una corriente de frecuencia de potencia de 100 A, lo que indica que tiene muy buenas características para soportar una corriente de alta frecuencia de potencia. 1.4.4. Rendimiento a Largo Plazo del LRM China, en la investigación del despeño a largo plazo de LRM, ha recolectado datos durante más de diez años sobre el cambio anual en las resistencias de puesta a tierra de electrodos usando LRM. Determinando que la resistencia de puesta a tierra tiene solamente una ligera variación. Sin embargo, si el LRM pierde su función después de un cierto período de tiempo, la resistencia de puesta a tierra aumentará y sería extremadamente difícil reemplazar el LRM. Por lo tanto, se espera que el LRM mantenga su resistividad sin cambios durante mucho tiempo. El rendimiento a largo plazo de LRM se puede obtener mediante la adición de algunos aditivos para jar su conductividad. Los aditivos que pueden jar su conductividad incluyen cemento Portland, carbón o una mezcla de ceniza de carbón y ceniza de carbón, materiales asfálticos y materiales químicos. 1.4.5. Método de construcción de LRM Existen varios métodos de construcción de LRM, la Figura 1.4.5.3 muestra diferentes métodos de construcción de LRM. Estos métodos pueden clasicarse en tres categorías: 1.4.5.1. Método llenado Este método se utiliza comúnmente en la construcción de un electrodo de tierra vertical. Tiene dos formas de construcción: a) El primero es cavar un agujero de una profundidad de 75 cm y conducir una o tres varillas de tierra en el fondo del agujero. A continuación, se vierte el LRM preparado en el agujero junto a las varillas. Finalmente, se procede a rellenar y comprimir la parte del terreno después de que el LRM se haya solidicado. b) El segundo es un método de perforación que se utiliza comúnmente en la conexión a tierra profunda. En este método se perfora un agujero con un diámetro mayor de 5cm y una profundidad que satisface el requisito de diseño. Entonces, se coloca la varilla en la parte inferior del agujero y luego se llena el agujero con LRM preparado. Finalmente, después de que el LRM se haya solidicado, el agujero se rellena con tierra y se comprime. Si la varilla de tierra es demasiado larga, se puede utilizar un tubo redondo de gran diámetro como electrodo de tierra vertical. A continuación, taladre algunos pequeños agujeros en la parte inferior de la tubería redonda, luego se procede a llenar el oricio con LRM utilizando una máquina de inyección de presión, después se usa un tapón de metal para cubrir la parte superior de la tubería de acero. La Figura 1.4.5.3(a) muestra una varilla de tierra vertical con el oricio relleno de LRM. La Figura 1.4.5.3(b) muestra un electrodo de tira. Si las grietas pueden ser formadas por una explosión en el agujero, a continuación, verter LRM en el agujero con una máquina de presión, lo que da un efecto mucho mejor en la disminución de la resistencia de puesta a tierra. 24 1.4.5.2. Método de penetración El método de penetración es comúnmente utilizado para electrodos de tierra incorporados. Como se muestra en la Figura 1.4.5.3(c), se agrega LRM líquido y penetra en la tierra que rodea al electrodo incorporado, o como se muestra en la Figura 1.4.5.3(d), se cava una ranura anular alrededor de la varilla de tierra vertical y se llena con LRM líquido. 1.4.5.3. Método de la zanja Este método es comúnmente utilizado en la construcción de dispositivos de tierra horizontales, tales como una varilla horizontal o la malla de un sistema de puesta a tierra. Para su construcción se procede a cavar una zanja y luego disponer de forma adecuada el electrodo o conductor de tierra. Se debe tener en cuenta que los conductores deben ser soportados por el LRM solidicado. Entonces el LRM se llena en la zanja para asegurarse de que todo el conductor de tierra sea recubierto por el LRM. Después de que el LRM se ha solidicado, la zanja se rellena con tierra y se comprime para evitar la exposición y la evaporación del agua. La Figura 1.4.5.3(e) muestra un método de la zanja que usa LRM para recubrir el conductor en horizontal y luego se rellena con tierra. La Figura 1.4.5.3(f ) muestra un método de zanja utilizado en la construcción de un electrodo de tierra horizontal tipo placa. Figura 1.4.3: Métodos de construcción usando LRM: (a) varilla vertical con el oricio relleno de LRM, (b) electrodo de tira, (c) se agrega LRM líquido y penetra en la tierra que rodea al electrodo incorporado, (d) una ranura anular excavado alrededor de una varilla vertical y luego se llena el LRM líquido, (e) método de la zanja que usa LRM para recubrir el electrodo horizontal y luego se rellena con tierra, (f ) método de la zanja usado en la construcción de un electrodo de tierra horizontal tipo placa [14]. En general, los métodos de construcción mencionados deben considerarse según el tipo de LRM, la forma del electrodo y la geología del sitio del proyecto. En sitios donde es difícil obtener agua, los polvos LRM secos se pueden verter directamente en la zanja alrededor del electrodo de tierra y el terreno debe ser rellenado y apisonado, lo que dará como resultado un buen efecto. 1.5. La Resistencia de Puesta a Tierra 8 impedancia de un sistema de puesta a tierra depende en gran medida de la resistividad del terreno, así como la conguración de la malla enterrada. Por lo general, el valor de la impedancia de un electrodo se mide en términos de resistencia porque la reactancia generalmente es despreciable con respecto al componente resistivo. 8 Es la suma de un componente resistivo y un componente reactivo. 25 La determinación del componente reactivo es necesario cuando el análisis se realiza para corrientes transitorias o de impulso, como es el caso de las descargas eléctricas. Así mismo, este valor puede ser muy signicativo en sistemas de puesta a tierra grandes o interconectados. 1.5.1. Valor teórico de la resistencia a tierra Los valores calculados o teóricos de la resistencia de un electrodo de puesta a tierra pueden variar con respecto al valor medido por las siguientes circunstancias: a) La insuciencia de los métodos analíticos utilizados en los cálculos de la resistencia. b) La resistividad del terreno en el momento de la medición de la resistencia, es diferente de la asumida en los cálculos. c) La falta exactitud en las mediciones de campo de la resistividad. Ya sea por la falta del número y dispersión de pruebas, variación en el espaciamiento de las sondas o debido a que el instrumento de medición no es el adecuado. d) Los objetos enterrados como rieles y tuberías metálicas, situados en las proximidades del terreno de prueba, pueden tener una inuencia considerable en los resultados de las mediciones. e) Las lecturas del medidor de pinza pueden contener un gran error si la reactancia en el circuito de prueba es signicativa comparada con la resistencia del circuito de prueba, o si los ltros son inadecuados para frecuencias de 50Hz/60Hz causadas por corrientes extraviadas. Este medidor está sujeto a errores causados por la reactancia en el circuito de prueba porque las frecuencias de prueba varían típicamente de 1 kHz a 3,4 kHz. Además, si hay bucles de tierra, el medidor de pinza no puede medir la resistencia de tierra correcta. La diferencia entre los valores medidos y calculados de la resistencia puede minimizarse si se obtienen las medidas de resistividad del terreno y resistencia de la malla en condiciones meteorológicas similares. Por lo que es recomendable realizar las mediciones de resistividad del terreno durante condiciones climáticas adversas, como la época de verano. 1.5.2. Medición de la Resistencia Antes de que una instalación eléctrica entre en servicio, por lo general se realiza una medición la resistencia de puesta a tierra y en el caso de las subestaciones, se realizan las mediciones de los potenciales superciales con el n de asegurarse que cumplen con los valores del diseño, ya que la resistencia de puesta a tierra puede variar con la estación a medida que cambian la temperatura, el contenido de humedad y la densidad del terreno. Por tal razón, la única manera de determinar la resistencia es medirla después de que el sistema haya sido completado [3], [18]. Los principios que se usan para la medición de la resistencia a tierra son básicamente los mismos que los utilizados para medir otros tipos de resistencias eléctricas. Los diversos métodos disponibles hacen uso de sondas auxiliares además del electrodo sometido a ensayo. 1.5.2.1. Método de dos puntos En el método de dos puntos, la resistencia a tierra del sistema se mide en serie con un electrodo auxiliar el cual deberá tener una resistencia despreciable en comparación con la resistencia del sistema de prueba. Entonces, el valor medido representa la resistencia a tierra del sistema de prueba. Por lo general, una aplicación de este método es medir la resistencia del sistema de puesta a tierra de prueba con respecto a una casa residencial cercana. Siendo así, se puede seleccionar el electrodo auxiliar de dos maneras: 26 Elementos Metálicos Los elementos metálicos que se encuentran bajo tierra como las tuberías que suministran agua pueden presentar una resistencia de alrededor de 1Ω, mientras que la resistencia de un sistema de puesta a tierra de una residencia se presume debería ser 25Ω siendo mucho mayor que la resistencia del electrodo auxiliar. En la Figura 1.5.2.1 se muestra el método de dos puntos utilizando un electrodo auxiliar, mediante un instrumento de medición que más adelante será descrito. Figura 1.5.1: Medida de la resistencia de tierra a dos puntos utilizando un instrumento especializado de medición [4]. Uso del neutro como electrodo auxiliar Es posible realizar la medición de tierra con el método de dos puntos utilizando como electrodo auxiliar el conductor de neutro de la compañía de suministro, conectando directamente en la toma de corriente o del cuadro de alimentación, por lo tanto la medida puede ser realizada directamente en la toma de corriente, entre el neutro y la tierra. En la Figura 1.5.2.1 se muestra el método de dos puntos usando como electrodo auxiliar el neutro del cuadro de alimentación. Figura 1.5.2: Medida de la resistencia de tierra a dos puntos desde el cuadro de alimentación [4]. El método de dos puntos, sin embargo, está expuesto a errores en su aplicación como los que se mencionan a continuación: a) Si la tubería que funciona como electrodo auxiliar está demasiado cerca al sistema de tierra de prueba, la resistencia mutua entre los dos puede ser una fuente de error. b) Si la resistencia de la puesta a tierra del sistema a prueba está en el rango de la resistencia del electrodo auxiliar. 27 Sin embargo, este método es una herramienta útil donde no es posible usar el método de tres puntos (por ejemplo en el centro histórico), mediante éste método generalmente se obtendrá un valor superior siendo una ventaja desde el punto de vista de la seguridad. 1.5.2.2. Método de tres puntos En este método se usan dos electrodos o picas auxiliares con sus resistencias designadas como Ry y Rz , mientras que la resistencia del electrodo o varilla en análisis se denomina Rx. Estas picas se colocan de tal manera que se forma un triángulo como se ilustra en la Figura 1.5.2.2, entonces se procede a medir la resistencia mediante un instrumento de medida especializado (no se inyecta Iprueba ). La resistencia entre cada par de electrodos se designa como R1, R2 y R3, donde: R1 = Rx + Ry + 0 R2 = Rx + 0 + Rz R3 = 0 + Ry + Rz Resolviendo las tres ecuaciones simultáneas para despejar Rx = Rx, se tiene: R1 + R2 + R3 2 (1.5.1) Por medio de la ecuación (1.5.1) se obtiene la resistencia a tierra del electrodo sometido a prueba. Figura 1.5.3: Método de tres puntos [18]. Consideraciones del método de tres puntos: a) Para una medición conable, los electrodos deben estar a una distancia sucientemente distante entre sí para minimizar las resistencias mutuas entre ellos. La separación de las picas debe ser por menos tres veces la profundidad de la varilla de prueba. b) Este método es adecuado para medir la resistencia de varillas de tierra aislados o pequeñas instalaciones de puesta a tierra. c) No es apropiado para la medición de instalaciones de baja resistencia. 28 1.5.2.3. Método de caída del potencial. En el método de caída de potencial se usan dos picas auxiliares conocidas como y pica de potencial pica de corriente que se posicionan en una misma dirección. Se inyecta una corriente constante entre el electrodo o varilla de tierra (G) y una pica de corriente (CP), luego se mide la tensión entre G y una pica de potencial (PP), como se muestra en la Figura 1.5.4. La pica de potencial normalmente se coloca en la misma dirección que la pica de corriente, pero se puede colocar en la dirección opuesta. Figura 1.5.4: Método de caída del potencial [6]. Para minimizar las inuencias interelectrodo debido a las resistencias mutuas, la pica de corriente se coloca a una distancia (D) que por lo general es al menos 5 veces la longitud de la varilla o 5 veces la diagonal máxima del sistema puesto a tierra bajo prueba. Mientras que la distancia X para la pica de potencial, comúnmente se toma el 62 % de la distancia D cuando están en la misma dirección (regla del 62 %). Cabe mencionar que para aplicar la regla del 62 % el terreno tiene que ser bastante uniforme y la varilla no debe tener conexiones externas. Este método puede estar sujeto a un error considerable si están presentes corrientes de tierra dispersas (a la misma frecuencia del medidor de prueba), o si las tuberías u otros conductores están enterrados cerca de la varilla de prueba. Una forma práctica de determinar si la pica de potencial está libre de inuencias de otros electrodos es obteniendo realizando varias mediciones de resistencia moviendo la pica de potencial entre la varilla y la pica de corriente. Se puede asumir que dos o tres lecturas consecutivas de resistencia constante representan el verdadero valor de resistencia. 1.5.2.4. Método de Clamp-on La medición de la resistencia de puesta a tierra por este método se lo realiza por medio de una pinza conocida como clamp sujetándolo al cable de derivación, como se muestra en la Figura 1.5.5. El medidor de sujeción induce un voltaje con una frecuencia denida, por lo general entre 1 kHz y 3.4 kHz, en el sistema de puesta a tierra que incluye a la varilla bajo estudio. El voltaje inducido genera una corriente (Iprueba ) que uye hacia el sistema de puesta a tierra, la cual es medida por la misma pinza. Entonces, el equipo de medición muestra en formato digital la resistencia que se obtiene mediante la ley de ohm. Para obtener un resultado con alto grado de precisión, la impedancia del sistema de neutro 29 multiaterrizado, debe ser signicativamente menor en comparación con la impedancia de la varilla, siendo así se puede asumir que es cero (Zeq=0). Además es importante que el circuito de prueba tenga una baja reactancia en comparación a la resistencia, debido a que la reactancia aumenta de forma signicante en respuesta a la frecuencia de la corriente de prueba pudiendo distorsionar en gran medida las lecturas de prueba. Figura 1.5.5: Medición de la resistencia mediante el método de clamp-on [6]. Este método es práctico y ampliamente utilizado para las líneas de transmisión y distribución. La principal ventaja de este método es que es rápido y fácil, ya que no se necesitan picas adicionales y no es necesario desconectar el electrodo de tierra bajo prueba del sistema. El método clamp-on también puede medir la corriente de fuga que uye a través del sistema. Este método no se puede utilizar en terrenos aislados, ya que no hay ruta de retorno. Así mismo, no puede usarse si existe una resistencia alternativa de menor resistencia que involucra el terreno, como con torres celulares que se observa en la Figura 1.5.6 . 30 Figura 1.5.6: Medición incorrecta de la resistencia de tierra por el método clamp-on [6]. Las torres celulares están conectadas a tierra en la base, con cada cable individual puesto a tierra y todos conectados juntos en un anillo. La corriente de prueba circula a través del conductor que conecta los elementos individuales (varillas de tierra) que componen el anillo. Siendo así que la pinza de sujeción no va a medir la resistencia de puesta a tierra del sistema, ya que en realidad se estaría midiendo la resistencia del conductor y de los puntos de unión, sean soldaduras o accesorios mecánicos. 1.5.2.5. Método de caída de potencia/clamp-on La resistencia de un electrodo de tierra también se puede medir combinando el método de caída del potencial y el método de sujeción, como se ilustra en la Figura 1.5.7. Los electrodos auxiliares (picas) de corriente y tensión se colocan de la misma manera requeridas por el método de caída de potencial. Para medir la parte de la corriente de prueba que uye hacia el sistema de puesta a tierra se usa un transformador de núcleo partido en cada pata de la torre. Entonces, la resistencia autónoma del sistema de puesta a tierra se determina por la relación de la tensión medida y la corriente de tierra medida. Este método puede ser usado especialmente para medir las resistencias de las estructuras de líneas de transmisión ya que no es necesario desconectar el cable de guarda. En el caso de una torre de cuatro patas se puede medir la resistencia midiendo cada pata para luego combinarlas para determinar las resistencia global de la estructura. También se puede medir con equipos que se colocan cuatro transformadores de núcleo dividido y se mide la resistencia simultáneamente. 31 Figura 1.5.7: Medición de la resistencia de una torre utilizando el método de caída de potencial y mediciones de corriente de fuga [6]. 1.5.2.6. Multímetro de puesta a tierra basado en computadora La medición de impedancia de tierra mediante multímetro de puesta a tierra basado en computadora se puede realizar a un sistema de conexión a tierra aislado o interconectado de una torre, poste o subestación. La medición consiste en instalar una pica de retorno de corriente y seis picas de detección de voltaje, como se muestra en la Figura 1.5.8. La pica de retorno de corriente se ubica a una distancia de al menos dos veces la diagonal máxima de la instalación. La primera pica de tensión en cada hilo se coloca usualmente a una distancia de 15 m de la malla de la subestación. Las distancias de las picas de voltaje restantes se colocan de forma similar tomando como referencia la primera pica. Se recomienda que las sondas de voltaje estén situadas lo más lejos posible de otras estructuras de tierra como por ejemplo las tuberías. Usualmente, estos tipos de multímetros presentan las siguientes opciones de medición: a) Impedancia de tierra (aislado o interconectado) b) Resistividad del terreno c) Impedancia de tierra de la torre (impedancia de tierra de torre/polo independiente sin desconexión del blindaje o cables de neutro) d) Tensión de contacto e) Tensión de paso f) Impedancia de tierra (impedancia de tierra de la subestación independiente sin desconexión del blindaje y cables de neutro) g) Tensión de transferencia 32 h) Baja impedancia/continuidad (prueba de integridad del conductor de la red de tierra de la subestación) Figura 1.5.8: Medida de impedancia de tierra mediante multímetro de tierra basado en computadora [6]. 33 Capítulo 2 IMPLEMENTACIÓN DE SISTEMAS DE PUESTA A TIERRA 2.1. Mediciones de campo de la resistividad La medición de la resistividad del terreno se realiza mediante el 1 telurómetro digital, marca Amprobe modelo GP-2 Geo Test que se muestra en la Figura 2.1.1. En este equipo portátil se obtienen los valores de la resistividad del terreno directamente por el método de cuatro puntos arreglo Wenner, disponiendo las picas como se muestra en la Figura 1.2.3(a). Figura 2.1.1: Telurómetro digital GP-2 Geo Test [17]. 1 También llamado terrómetro o Megger, es un dispositivo que se utiliza para medir la resistividad y resistencia de los sistemas puestos a tierra. 34 Las mediciones son realizadas en 16 terrenos ubicados en una zona rural del Cantón Cuenca, debido a las grandes áreas disponibles para las mediciones de campo. Mediante el método Wenner se realiza las mediciones con un espaciamiento de las picas de 1m, 2m y 3m, así mismo cada medición se realiza en cuatro direcciones como se muestra en la Figura 2.1.2 para minimizar la inuencia en las lecturas en caso de existir estructuras o piezas metálicas enterradas en el área de estudio. Figura 2.1.2: Direcciones para las mediciones de las resistividades del terreno. 2.1.1. Resultados de las mediciones de la resistividad del terreno En el cuadro 2.1 se observan las mediciones de la resistividad del terreno 1. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 11.14 10.63 11.96 12.03 11.44 2 11.42 11.27 11.51 12.38 11.65 3 13.92 15.70 14.08 12.57 14.07 Separación [m] Tabla 2.1: Valores de resistividad medidos en el terreno 1. En el cuadro 2.2 se observan las mediciones de la resistividad del terreno 2. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 19.27 16.75 17.01 18.64 17.92 2 17.65 17.54 16.26 16.95 17.10 3 17.68 17.08 16.09 17.37 17.06 Separación [m] Tabla 2.2: Valores de resistividad medidos en el terreno 2. En el cuadro 2.3 se observan las mediciones de la resistividad del terreno 3. 35 Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 25.60 24.30 22.10 23.80 23.95 2 23.90 22.60 23.80 22.00 23.08 3 22.80 22.40 21.80 22.60 22.40 Separación [m] Tabla 2.3: Valores de resistividad medidos en el terreno 3. En el cuadro 2.4 se observan las mediciones de la resistividad del terreno 4. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 22.90 27.80 24.00 27.40 25.53 2 27.30 28.90 25.70 29.30 27.80 3 28.00 29.40 27.70 28.40 28.38 Separación [m] Tabla 2.4: Valores de resistividad medidos en el terreno 4. En el cuadro 2.5 se observan las mediciones de la resistividad del terreno 5. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 28.20 26.40 23.40 22.60 25.15 2 28.10 25.90 27.80 25.60 26.85 3 37.40 33.50 40.60 35.80 36.83 Separación [m] Tabla 2.5: Valores de resistividad medidos en el terreno 5. En el cuadro 2.1.1 se observan las mediciones de la resistividad del terreno 6. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 28.70 32.50 NA 33.80 31.67 2 30.80 32.60 NA 33.60 32.33 3 NA NA NA NA 31.90 Separación [m] Tabla 2.6: Valores de resistividad medidos en el terreno 6. NA: Mediciones no realizadas por falta de espacio para la colocación de las picas. En el cuadro 2.7 se observan las mediciones de la resistividad del terreno 7. 36 Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 25.00 26.40 24.90 27.60 25.98 2 28.60 33.60 32.30 31.50 31.50 3 46.60 45.20 55.30 41.90 47.25 Separación [m] Tabla 2.7: Valores de resistividad medidos en el terreno 7. En el cuadro 2.8 se observan las mediciones de la resistividad del terreno 8. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 40.60 41.70 40.50 44.00 41.70 2 44.20 45.20 44.10 44.90 44.60 3 46.30 45.80 46.20 46.20 46.13 Separación [m] Tabla 2.8: Valores de resistividad medidos en el terreno 8. En el cuadro 2.1.1 se observan las mediciones de la resistividad del terreno 9. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 40.00 46.20 49.90 44.70 45.20 2 49.20 54.60 53.80 54.00 52.90 3 NA 63.10 61.70 59.10 61.30 Separación [m] Tabla 2.9: Valores de resistividad medidos en el terreno 9. NA: Mediciones no realizadas por falta de espacio para la colocación de las picas. En el cuadro 2.10 se observan las mediciones de la resistividad del terreno 10. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 43.10 54.50 49.90 46.60 48.53 2 57.50 56.30 58.00 57.50 57.33 3 81.40 79.40 80.30 86.00 81.78 Separación [m] Tabla 2.10: Valores de resistividad medidos en el terreno 10. En el cuadro 2.11 se observan las mediciones de la resistividad del terreno 11. 37 Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 88.40 82.20 79.10 84.00 83.58 2 97.20 87.20 91.00 93.60 92.25 3 100.80 93.10 93.80 96.50 96.05 Separación [m] 1 Tabla 2.11: Valores de resistividad medidos en el terreno 11. En el cuadro 2.12 se observan las mediciones de la resistividad del terreno 12. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 87.30 83.70 <u.10 83.10 86.30 2 105.90 97.30 102.00 106.90 103.03 3 108.80 109.50 108.10 108.80 108.80 Separación [m] Tabla 2.12: Valores de resistividad medidos en el terreno 12. En el cuadro 2.1.1 se observan las mediciones de la resistividad del terreno 13. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 105.10 103.40 109.00 105.10 105.65 2 117.60 109.10 106.90 118.40 113.00 3 NA 105.70 107.30 108.50 107.17 Separación [m] Tabla 2.13: Valores de resistividad medidos en el terreno 13. NA: Mediciones no realizadas por falta de espacio para la colocación de las picas. En el cuadro 2.14 se observan las mediciones de la resistividad del terreno 14. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 111.60 122.90 94.30 100.20 107.25 2 123.00 134.40 112.80 116.10 121.58 3 104.80 124.80 102.20 108.00 109.95 Separación [m] Tabla 2.14: Valores de resistividad medidos en el terreno 14. En el cuadro 2.15 se observan las mediciones de la resistividad del terreno 15. 38 Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 149.20 144.80 150.80 146.40 147.80 2 189.00 175.50 178.10 181.00 180.90 3 174.10 176.20 178.40 175.90 176.15 Separación [m] Tabla 2.15: Valores de resistividad medidos en el terreno 15. En el cuadro 2.16 se observan las mediciones de la resistividad del terreno 16. Resistividad Resistividad Resistividad Resistividad Resistividad dirección 1 dirección 2 dirección 3 dirección 4 Promedio [Ω · m] [Ω · m] [Ω · m] [Ω · m] [Ω · m] 1 156.00 146.70 158.60 161.70 155.75 2 184.20 178.70 178.20 183.60 181.18 3 199.00 181.50 191.70 189.80 190.50 Separación [m] Tabla 2.16: Valores de resistividad medidos en el terreno 16. Se puede observar que la mayoría de terrenos tiene variaciones de resistividad relativamente pequeños, siendo así que a los mismos se les puede considerar como terrenos homogéneos. 2.2. Modelado de los terrenos En este trabajo se realiza el modelamiento del terreno para obtener una resistividad aparente mediante el modelo de terreno uniforme usando la ecuación (1.2.5), y mediante el método gráco Sunde descrito en el inciso 1.2.4, el procedimiento se detalla en (ANEXO A). En la Tabla 2.17 se observan los valores de resistividad aparente de cada terreno medido, calculados mediante los dos métodos, además se procede a aproximar a un valor inmediatamente superior de la resistividad. Terreno T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T11 T12 T13 T14 T15 T16 Resistividad aparente Resistividad aparente por el modelo de por el método terreno uniforme gráco sunde [Ω · m] 12.38 ≈ 13 17.36 ≈ 18 23.14 ≈ 24 27.13 ≈ 28 29.61 ≈ 30 31.97 ≈ 32 34.91 ≈ 35 44.14 ≈ 45 53.13 ≈ 54 62.54 ≈ 63 90.63 ≈ 91 99.38 ≈ 100 108.61 ≈ 109 112.93 ≈ 113 168.28 ≈ 169 175.81 ≈ 176 [Ω · m] 13.38 ≈ 14 17.38 ≈ 18 22.99 ≈ 23 27.31 ≈ 28 31.94 ≈ 32 31.67 ≈ 32 36.37 ≈ 37 44.62 ≈ 45 56.50 ≈ 57 65.02 ≈ 66 90.26 ≈ 91 102.70 ≈ 103 105.65 ≈ 106 107.25 ≈ 108 168.49 ≈ 169 180.67 ≈ 181 Tabla 2.17: Resultados del modelamiento de los terrenos. 39 2.3. Diseño de sistemas de puesta a tierra Algunas empresas eléctricas de distribución como la Empresa Eléctrica de Quito S.A., Empresa Eléctrica Regional Centro Sur C.A., y Empresas Eléctricas de Colombia estudiadas en [12] toman un valor de referencia de 25 ohmios para la puesta a tierra especialmente para el neutro de la red de baja tensión. Sin embargo, por la creciente demanda de energía eléctrica, se estima que este valor tiende a disminuir. Por tal motivo, en este proyecto se pretende obtener una resistencia de puesta a tierra de 15 ohmios o menos mediante la implementación de diferentes diseños. Además se realizan implementaciones de diseños adicionales para vericar la formulación usada. Los diseños que se presentan a continuación se realizan para sistemas con neutros conectados a tierra con corrientes de falla por debajo de 1000A, a los cuales según la norma IEEE Std 802013 señala que no es viable la eliminación de potenciales de paso y contacto. Mientras que para corrientes de falla a tierra por encima de 1000A, se debe instalar sistemas de puesta a tierra de grandes dimensiones para cumplir con los usuales requisitos de potencial de paso y contacto [8]. Sin embargo, se realiza un diseño en el que se pueda analizar cada paso descrito por la norma IEEE Std 80-2013 para cumplir con los requisitos de tensión de paso y contacto tolerables para el cuerpo humano. 2.3.1. Área de estudio Las dimensiones de los terrenos medidos tienen una longitud de 9m largo y de 9m de ancho dando un área total del terreno de 81m2 . En la Tabla 2.18 se da a conocer la resistividad aparente de cada terreno seleccionado para este estudio. Observándose que para la gran mayoría solo se requiere un modelo de suelo uniforme, excepto el terreno 16 que se toma como referencia el valor de la resistividad aparente obtenido mediante el método gráco Sunde, debido a los valores de resistividad muy variados en este terreno. Terreno Resistividad aparente [Ω · m] T1 13 T2 18 T3 24 T4 28 T5 30 T6 32 T7 35 T8 45 T9 54 T10 63 T11 91 T12 100 T13 109 T14 113 T15 169 T16 181 Tabla 2.18: Valores seleccionados de resistividad aparente de los terrenos. 40 2.3.2. Conductor Para realizar el cálculo del calibre del conductor se tiene como datos las corrientes de cortocircuito que se muestran en la Tabla 2.3.2, correspondiente al poste con numeración 262976 ubicado a 14km de la subestación, en la zona rural de estudio (Sinincay), perteneciente al alimentador 0523 (22 KV) de la subestación 05 El Arenal, bajo concesión de la Tipo de falla LLT-AB LLT-BC LLT-CA LT-A LT-B LT-C EERCS C.A. Tensión Tensión Corriente Corriente [kV ] [Grad] [kA] [Grad] A 4.15 -118.32 0.83 -117.93 B 4.17 122.4 0.83 122.28 C 4.14 2.72 0.83 2.44 A 6.86 -130.7 0.76 -95.74 Fase LLLT 2 B 5.14 157.21 0.7 100.67 C 13.36 38.76 0 0 A 13.36 -81.24 0 0 B 6.85 109.48 0.76 144.56 C 5.15 37.33 0.7 -19.02 A 5.09 -83.26 0.76 24.53 B 13.35 158.72 0 0 C 6.8 -10.28 0.7 -139.29 A 7.9 -107.39 0.4 -107.39 B 14.4 153.47 0 0 C 12.44 43.62 0 0 A 12.44 -76.38 0 0 B 7.9 132.76 0.39 132.76 C 14.4 33.49 0 0 A 14.4 -86.49 0 0 B 12.43 163.61 0 0 C 7.9 12.9 0.39 12.9 Tabla 2.19: Resumen durante la falla Fuente: EERCS C.A.: Soporte Informático - Análisis Técnico If = 830A. Sin embargo, en este trabajo se toma como If = 1000A. Según la Tabla 1.2, considerando X/R=10, factor de decremento es Df = 1,026. El cálculo de la máxima La mayor corriente de falla es de referencia una corriente de falla a tierra de y una duración de falla tf = 0,5s, el IF se realiza corriente de falla asimétrica mediante la ecuación (2.3.1), multiplicando el factor de decremento por la corriente máxima de falla a tierra. IF = If × Df (2.3.1) Se reemplazan los valores y tendiendo lo siguiente IF = 1000A × 1,026 = 1026A La corriente obtenida se usa para la determinación del mínimo diámetro de los conductores de puesta a tierra. Para la implementación de los sistemas de puesta a tierra se cuenta con conductor de cobre comercial trenzado duro con una conductividad del material del de 1084ºC 97 % y una temperatura de fusión según la Tabla 1.3.2.1. Sin embargo, para una mayor seguridad se procede a calcular en la peor condición, seleccionando para el análisis un conductor de alambre de acero con revestimiento 2 Empresa Eléctrica Regional Centro Sur C.A. 41 de cobre con una conductividad del máxima de fundición de 450ºC 30 %, una temperatura ambiente de 30ºC y una temperatura (Para una conexión Exotérmica). Entonces, la sección transversal del conductor se calcula con la ecuación (1.3.1) teniendo como resultado lo siguiente: Amm2 = 5,61mm2 Según la Tabla C.2 (ANEXO C), el calibre del cable para esta sección de conductor es el alambre de acero con revestimiento de cobre #8 AWG; sin embargo, en el presente trabajo se usa conductor de cobre desnudo #2 AWG con sección transversal de 33,62mm2 . Ya que en varias empresas eléctricas de distribución como las que se ven en [5] y [12] (Empresa Eléctrica de Quito S.A., Empresa Eléctrica Regional Centro Sur C.A., Empresa Eléctrica Regional del Sur S.A. y de Empresas Eléctricas de Colombia), utilizan un conductor de cobre desnudo que varía entre #4 AWG y #2 AWG, para los sistemas de puesta a tierra. 2.3.3. Tensiones Tolerables Si bien los sistemas de puesta a tierra pueden ajustarse para eliminar los potenciales de contacto peligrosos mediante la supresión de las corrientes de cortocircuito a tierra, esto no suele exigirse a los sistemas con neutros conectados a tierra con corrientes de falla menores a 1000A, porque no parece viable. Para corrientes de falla a tierra por encima de 1000 A, se deben instalar sistemas de puesta a tierra de grandes dimensiones para cumplir con los usuales requisitos de potenciales de paso y de contacto [8]. En el presente proyecto se realiza un diseño en el terreno 2 en el que se pueda analizar cada paso descrito por la norma IEEE Std 80-2013 para cumplir con los requisitos de tensión de paso y contacto tolerables por el cuerpo humano. Los demás diseños que se realizan van dirigidos a sistemas con bajos niveles de corrientes de falla a tierra (inferiores a 1000A). El terreno 2 que cuenta con una resistividad aparente de 18Ω · m. La norma IEEE Std. 80-2013 determina la importancia de aumentar el límite de las tensiones de paso y de contacto tolerables, con la distribución de una pequeña capa supercial de grava, que normalmente tiene un espesor entre 0.10m y 0.15m. Para el diseño se considera que el espesor de la grava o piedra triturada sea de hs = 0,10m, que cuenta con una resistividad de ρs = 3000Ω · m. Mediante la Cs = 0,69. Con un tiempo de despeje de falla de ts = 0,5s, se calculan se tiene ecuación (1.3.6) las tensiones de paso y de contacto tolerables para una persona con peso corporal de 70 kg usando las ecuaciones (1.3.3) y (1.3.5). Epaso70kg = 2985,73V Econtacto70kg = 912,96V 2.3.4. Diseños básicos y resistencia de puesta a tierra Como ya se mencionó, el propósito de los diseños en este trabajo es obtener una resistencia de puesta a tierra de 15 ohmios, en terrenos con diferentes valores de resistividades. Así mismo, se ha realizado diseños adicionales para vericar si la formulación usada es válida. El diseño bajo análisis de potenciales peligrosos para el cuerpo humano puede observar en el Cuadro 2.3.4 correspondiente al diseño T2.3. Los diseños están conformados por varillas de cobre copperweld de 1.8m x 5/8 y de 2.4m x 5/8, conductores de cobre trenzado desnudo #2 AWG a una profundidad h = 0,25m. Las conguraciones involucran: 1 varilla en vertical, 2 varillas en línea, 3 varillas en línea, 3 varillas en triángulo y mallas cuadradas con 4 varillas en las esquinas, todos separadas a una distancia d. 42 Además se calcula la resistencia de puesta a tierra de cada diseño mediante las fórmulas presentadas en el inciso 1.3.5. En la tabla 2.3.4 se observa el diseño de puesta a tierra para el terreno 1 con una resistividad aparente de 13 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T1.1 1 Varilla 1.8[m] 6.67 x x Tabla 2.20: Diseño del sistema de puesta a tierra para el terreno 1. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 2 con una resistividad aparente de 18 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T2.1 1 Varilla 1.8[m] 9.23 T2.2 2 Varillas 1.8[m] 3.57 x d=7[m] x x x x x x x T2.3 4 Varillas 1.8[m] x d=4[m] 1.91 x Tabla 2.21: Diseños de sistemas de puesta a tierra para el terreno 2. En la tabla 2.3.4 se observa el diseño de puesta a tierra para el terreno 3 con una resistividad aparente de 24 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T3.1 1 Varilla 2.4[m] 9.69 x x Tabla 2.22: Diseño del sistema de puesta a tierra para el terreno 3. 43 En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 4 con una resistividad aparente de 28 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T4.1 1 Varilla 1.8[m] 14.37 T4.2 2 Varillas 1.8[m] 7.84 x d=3[m] x x x x x x x T4.3 3 Varillas 1.8[m] x d=3[m] 5.37 x Tabla 2.23: Diseños de sistemas de puesta a tierra para el terreno 4. En la tabla 2.3.4 se observa el diseño de puesta a tierra para el terreno 5 con una resistividad aparente de 30 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T5.1 1 Varilla 1.8[m] 15.39 x x Tabla 2.24: Diseño del sistema de puesta a tierra para el terreno 5. En la tabla 2.3.4 se observa el diseño de puesta a tierra para el terreno 6 con una resistividad aparente de 32 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T6.1 1 Varilla 2.4[m] 12.92 x x Tabla 2.25: Diseño del sistema de puesta a tierra para el terreno 6. 44 En la tabla 2.3.4 se observa el diseño de puesta a tierra para el terreno 7 con una resistividad aparente de 35 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T7.1 1 Varilla 2.4[m] 14.14 x x Tabla 2.26: Diseño del sistema de puesta a tierra para el terreno 7. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 8 con una resistividad aparente de 45 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T8.1 1 Varilla 1.8[m] 23.09 T8.2 2 Varillas 1.8[m] 12.60 x d=3[m] x x x x x x x T8.3 1 Varilla 2.4[m] 18.17 T8.4 2 Varillas 2.4[m] 10.56 x d=3[m] x x x x x x x T8.5 3 Varillas 2.4[m] x d=3[m] 7.51 x Tabla 2.27: Diseños de sistemas de puesta a tierra para el terreno 8. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 9 con una resistividad aparente de 54 Ω · m. 45 Resistencia Diseño Conguración Descripción Calculada [Ω] x x 1 Varilla 1.8[m] 27.70 T9.2 2 Varillas 1.8[m] 13.76 x d=4[m] T9.1 x x x x x Tabla 2.28: Diseños de sistemas de puesta a tierra para el terreno 9. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 10 con una resistividad aparente de 63 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T10.1 1 Varilla 1.8[m] 32.32 T10.2 2 Varillas 1.8[m] 17.64 x d=3[m] x x x x x x x T10.3 2 Varillas 1.8[m] x d=4[m] 16.05 x x x T10.4 2 Varillas 1.8[m] x d=5[m] 14.69 x Tabla 2.29: Diseños de sistemas de puesta a tierra para el terreno 10. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 11 con una resistividad aparente de 91 Ω · m. 46 Resistencia Diseño Conguración Descripción Calculada [Ω] x x 1 Varilla 1.8[m] 46.69 T11.2 2 Varillas 1.8[m] 25.48 x d=3[m] T11.1 x x x x x x x T11.3 2 Varillas 1.8[m] x d=4[m] 23.19 x x x T11.4 2 Varillas 1.8[m] x d=5[m] 21.22 x x x T11.5 3 Varillas 1.8[m] x d=3[m] 17.46 x x x T11.6 3 Varillas 1.8[m] x d=4[m] 15.24 x x x T11.7 3 Varillas 1.8[m] x d=3[m] 15.88 x x x T11.8 3 Varillas 1.8[m] x d=4[m] 13.45 x Tabla 2.30: Diseños de sistemas de puesta a tierra para el terreno 11. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 12 con una resistividad aparente de 100 Ω · m. 47 Resistencia Diseño Conguración Descripción Calculada [Ω] x x 1 Varilla 1.8[m] 51.30 T12.2 2 Varillas 1.8[m] 25.48 x d=4[m] T12.1 x x x x x x x T12.3 3 Varillas 1.8[m] x d=4[m] 16.75 x x x T12.4 3 Varillas 1.8[m] x d=4[m] 14.78 x Tabla 2.31: Diseños de sistemas de puesta a tierra para el terreno 12. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 13 con una resistividad aparente de 109 Ω · m. 48 Resistencia Diseño Conguración Descripción Calculada [Ω] x x 1 Varilla 1.8[m] 55.92 T13.2 2 Varillas 1.8[m] 30.52 x d=3[m] T13.1 x x x x x x x T13.3 3 Varillas 1.8[m] x d=3[m] 20.92 x x x T13.4 3 Varillas 1.8[m] x d=3[m] 19.02 x x x T13.5 3 Varillas 1.8[m] x d=5[m] 13.95 x x x T13.6 4 Varillas 1.8[m] x d=3[m] 13.74 x x x T13.7 1 Varilla 2.4[m] 44.02 T13.8 2 Varillas 2.4[m] 23.64 x d=4[m] x x x x x x x T13.9 3 Varillas 2.4[m] x d=4[m] 16.14 x x x T13.10 3 Varillas 2.4[m] x d=4[m] 14.64 x Tabla 2.32: Diseños de sistemas de puesta a tierra para el terreno 13. 49 En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 14 con una resistividad aparente de 113 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x T14.1 1 Varilla 1.8[m] 57.97 T14.2 2 Varillas 1.8[m] 31.64 x d=3[m] x x x x x x x T14.3 2 Varillas 1.8[m] x d=4[m] 28.79 x x x T14.4 2 Varillas 1.8[m] x d=6[m] 24.22 x x x T14.5 3 Varillas 1.8[m] x d=3[m] 21.69 x x x T14.6 3 Varillas 1.8[m] x d=5[m] 16.79 x x x T14.7 3 Varillas 1.8[m] x d=3[m] 19.72 x x x T14.8 3 Varillas 1.8[m] x d=5[m] 14.46 x x x T14.9 4 Varillas 1.8[m] x d=3[m] 14.24 x Tabla 2.33: Diseños de sistemas de puesta a tierra para el terreno 14. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 15 con una resistividad 50 aparente de 169 Ω · m. Resistencia Diseño Conguración Descripción Calculada [Ω] x x 1 Varilla 1.8[m] 86.70 T15.2 2 Varillas 1.8[m] 43.06 x d=4[m] T15.1 x x x x x x x T15.3 1 Varilla 2.4[m] 68.25 T15.4 2 Varillas 2.4[m] 34.12 x d=5[m] x x x x x x x T15.5 3 Varillas 2.4[m] x d=5[m] 22.56 x x x T15.6 3 Varillas 2.4[m] x d=5[m] 20.01 x x x T15.7 4 Varillas 2.4[m] x d=5[m] 14.38 x Tabla 2.34: Diseños de sistemas de puesta a tierra para el terreno 15. En la tabla 2.3.4 se observan los diseños de puesta a tierra para el terreno 16 con una resistividad aparente de 181 Ω · m. 51 Resistencia Diseño Conguración Calculada Descripción [Ω] x x 1 Varilla 1[m] 150.22 1 Varilla 1.8[m] 92.86 T16.3 2 Varillas 1.8[m] 38.80 x d=6[m] T16.1 x x x x T16.2 x x x x x x x T16.4 3 Varillas 1.8[m] x d=6[m] 24.16 x x x T16.5 3 Varillas 1.8[m] x d=6[m] 20.42 x x x T16.6 4 Varillas 1.8[m] x d=6[m] 14.59 x x x T16.7 73.10 1 Varilla 2.4[m] x x Tabla 2.35: Diseños de sistemas de puesta a tierra para el terreno 16. 2.3.5. Corriente máxima de malla Considerando que el factor de división de la corriente de falla sf = 1, y aplicando la ecuación (1.3.25) se tiene que: IG = 1026A 2.3.6. Potencial Máximo de la Malla (GPR) GPR se obtiene mediante la ecuación (1.3.26) teniendo como resultado: GP R = 1959,66V Como se puede observar el valor de la elevación del potencial de tierra está por encima del valor de la tensión de contacto tolerable por el cuerpo humano, por lo que es necesario continuar con el 52 diseño. GP R = 1959,66[V ] > Econtacto70kg = 912,96[V ] 2.3.7. Tensiones de paso y de contacto reales Para realizar los cálculos de las tensiones de paso y de contacto, se necesita conocer los parámetros del diseño que se muestran en la Tabla 2.3.7. Denominación Valor Resistividad del terreno 2 ρ = 18Ω · m h = 0,25m d = 6,543mm D = 4m Lr = 1,8m LR = 7,2m IG = 1026A Lx = 4m Profundidad de la malla Diámetro del conductor de la malla Espaciamiento entre conductores paralelos Longitud de cada varillas de aterrizaje Longitud total de todas las varillas de aterrizaje Corriente máxima de malla Longitud máxima de los conductores de malla en dirección de x Longitud máxima de los conductores de malla en dirección de Ly = 4m y Longitud total del conductor horizontal de la malla Longitud perimetral de la malla LC = 16m Lp = 16m Tabla 2.36: Datos para el cálculo de las tensiones de paso y de contacto reales. Mediante estos parámetros de la malla, se procede a calcular los factores que se muestran en la Tabla 2.3.7, por medio de las ecuaciones descritas en el inciso 1.3.8. Denominación Valor Calculado Número efectivo de conductores paralelos en una n=2 malla Longitud efectiva del conductor para la tensión de Ls = 18,12 paso Factor de espaciamiento para la tensión de paso Factor de correción para la geometría de la malla Longitud efectiva del conductor de la malla para la Ks = 0,71 Ki = 0,94 LM = 29,96m tensión de contacto Factor de ponderación correctivo que se ajusta para Kii = 1 efectos de conductores internos Factor de ponderación correctivo que se hace Kh = 1,12 hincapié en los efectos de la profundidad de la malla Factor de espaciamiento para la tensión de contacto Km = 0,91 Tabla 2.37: Datos para el cálculo de la tensión de paso y de contacto reales de la malla cuadrada del diseño T2.3. Mediante los parámetros de la malla detallados en la Tabla 2.3.7, y los resultados obtenidos en la Tabla 2.3.7 se procede a calcular las tensiones de paso y de contacto reales con las ecuaciones (1.3.27) y (1.3.31) respectivamente. Epaso = 681,67[V ] 53 Econtacto = 526,59[V ] 2.3.8. Control de seguridad Para que el diseño cumpla con los requisitos de la norma IEEE Std 80-2013, la tensión de contacto real Em tiene que ser menor que la tensión de contacto tolerable que la tensión de paso real Es Econtacto70kg , mientras Epaso70kg . tiene que ser menor que la tensión de paso tolerable Econtacto = 526,59[V ] < Econtacto70kg = 912,96[V ] Epaso = 681,67[V ] < Epaso70kg = 2985,73[V ] Como se puede constatar el diseño cumple con los requisitos, y está listo para su implementación. 2.4. Tratamiento del terreno para reducir la resistividad Una solución alternativa para reducir la resistencia especialmente en terrenos donde la conductividad es muy baja, es mediante el tratamiento del suelo como se indica en el inciso 1.4. En este proyecto se usan tres métodos para la reducción de la resistencia a tierra, mediante 3 Material de Mejora del Suelo ( GEM, por sus siglas en inglés) en forma de cemento mezclado con agua de marca BenzoElectric, con el mejorador de tierra GEM de forma seco de marca Cadweld y mediante un electrodo químico marca Parres. 2.4.1. Material de mejora del suelo seco (GEM Cadweld) En la Figura 2.4.1 se observa el material de mejora del suelo de la marca Cadweld que consta de una bolsa de 25 libras (11.36 kg). Este material tiene las siguientes características: No es un material corrosivo Está compuesto de polvo de carbón (cemento Porland, el cual al fraguar se endurece y transforma en concreto conductivo requiriendo 3 días para solidicarse) No necesita mantenimiento (no necesita recibir agua para mantener su conductividad) No se disuelve ni descompone a lo largo del paso del tiempo (es permanente y conserva su resistencia a tierra). Fácil instalación Puede ser mezclado o instalado ya sea húmedo o en su forma seca. La instalación del GEM en forma seca es preferible para aplicaciones de varillas verticales. No contamina el suelo 3 Es un material de conductividad superior que mejora la efectividad del sistema de puesta a tierra y se lo aplica alrededor de los conductores y varillas de puesta a tierra. 54 Figura 2.4.1: Mejorador de tierra GEM marca Cadweld [1]. 2.4.1.1. Método de instalación La implementación del GEM en varillas verticales usualmente no es posible tener una instalación tal como lo indican los manuales [1], ya que en los terrenos bajo prueba se puede encontrar con rocas o piedra triturada, dicultando la excavación del agujero en su totalidad. Es por ello, que para este trabajo se realiza la instalación del GEM Cadweld en varillas verticales de la siguiente manera: 1. Se perfora un agujero de 20 cm de diámetro y una profundidad de aproximadamente 1.10m. 2. Se coloca el electrodo en el centro del agujero y se lo entierra hasta que el extremo superior de la varilla quede a unos 15cm del nivel del terreno. Se realiza la conexión con el conductor. 3. Se vacía una bolsa de GEM (25 libras) alrededor del electrodo, llenando completamente el GEM en el agujero alrededor del electrodo. 4. Se vierte de 1.4 a 2 galones (5.7 a 7.6 litros) de agua por bolsa. 5. Esperar a que el GEM endurezca aproximadamente una hora antes de rellenar la parte superior de agujero con la tierra que se sacó del mismo. 6. En tres días se puede medir la resistencia del sistema de puesta a tierra, sin embargo mediante las pruebas de campo se recomienda extender este tiempo a 15 días debido a que se ha notado una reducción de la resistencia de tierra en ese lapso de tiempo. 2.4.1.2. Implementación del GEM Cadweld La implementación de este mejorador de suelo se lo realiza en algunos diseños de puesta a tierra presentados anteriormente, para poder determinar el benecio de su implementación. En las siguientes tablas se presentan las implementaciones del GEM Cadweld. En la Tabla 2.4.1.2 se observa la implementación del GEM Cadweld en el terreno 8. 55 Diseño Conguración Descripción x x 1 Varilla 1.8[m] T8.1G GEM Cadweld x x x 2 Varillas 1.8[m] x T8.2G d=3[m] x GEM Cadweld x Tabla 2.38: Implementación del GEM Cadweld en el terreno 8. En la Tabla 2.4.1.2 se observa la implementación del GEM Cadweld en el terreno 14. 56 Diseño Conguración Descripción x x 1 Varilla 1.8[m] T14.1G GEM Cadweld x x x 2 Varillas 1.8[m] x T14.2G d=3[m] x GEM Cadweld x x x 2 Varillas 1.8[m] T14.3G d=4[m] x GEM Cadweld x x x 2 Varillas 1.8[m] T14.4G d=6[m] x GEM Cadweld x x x 3 Varillas 1.8[m] T14.5G d=3[m] x GEM Cadweld x x x 3 Varillas 1.8[m] T14.6G d=5[m] x GEM Cadweld x x x 3 Varillas 1.8[m] T14.7G d=3[m] x GEM Cadweld x x 3 Varillas 1.8[m] x T14.8G d=5[m] x GEM Cadweld x x x 4 Varillas 1.8[m] T14.9G d=3[m] x GEM Cadweld x Tabla 2.39: Implementación del GEM Cadweld en el terreno 14. En la Tabla 2.4.1.2 se observa la implementación del GEM Cadweld en el terreno 15. 57 Diseño Conguración Descripción x 2 Varillas 1.8[m] x T15.2G d=4[m] x GEM Cadweld x Tabla 2.40: Implementación del GEM Cadweld en el terreno 15. 2.4.2. Material de mejora del suelo premezclado (GEM BenzoElectric) En la Figura 2.4.2 se puede observar la bolsa de 12kg del GEM marca BenzoElectric. Figura 2.4.2: Mejorador de tierra GEM marca BenzoElectric El GEM BenzoElectric tiene las siguientes características: Facilidad de aplicación Facilidad en su reactivación Estabilidad (mantener la misma resistencia durante varios años) No es corrosivo Químicamente estable en el suelo No es tóxico Al igual que en este trabajo, en [13] se puede observar la aplicación de este material en una malla pequeña de puesta a tierra. 58 2.4.2.1. Método de instalación La instalación del GEM BenzoElectric para el presente trabajo se realiza de la siguiente manera: 1. Se realiza una perforación de 1.10m aproximadamente, con un diámetro aproximado de 20cm. Las varillas usadas en este trabajo tienen una longitud de 1.8m y de 2.4m, una excavación del agujero de su misma longitud sería lo ideal, sin embargo eso no es posible en la práctica ya que en los terrenos bajo prueba se encuentran rocas o piedra triturada a diferentes profundidades dicultando la excavación del agujero a partir de los 1.10m recomendados. 2. En algunos casos, es necesario usar un tubo de aproximadamente 20cm para rellenar el diámetro excesivo del agujero. Luego se retira el tubo teniendo un agujero ideal para el relleno del GEM, como se muestra en la Figura 2.4.2.1. 3. Se mezcla una bolsa de GEM BenzoElectric con agua, usando una cubeta , obteniéndose una solución gelatinosa. 4. Rellenar el agujero con la solución mezclada. 5. Colocar los electrodos en el centro del agujero hasta tener una distancia de 15cm de la supercie del terreno. 6. Realizar la conexión del conductor con el electrodo. 7. Reponer la parte del suelo retirado y compactar. Figura 2.4.3: Excavación del agujero para la implementación del GEM. 59 2.4.2.2. Implementación del GEM BenzoElectric En las siguientes tablas se presentan las implementaciones del GEM BenzoElectric en una muestra de terrenos y conguraciones presentadas anteriormente, para que en lo posterior se pueda determinar el benecio de su implementación. En la Tabla 2.4.2.2 se observa la implementación del GEM BenzoElectric en el terreno 2. Diseño Conguración Descripción x x 1 Varilla 1.8[m] T2.1G GEM BenzoElectric x x x x 2 Varillas 1.8[m] T2.2G d=7[m] x GEM BenzoElectric x Tabla 2.41: Implementación del GEM BenzoElectric en el terreno 2. En la Tabla 2.4.2.2 se observa la implementación del GEM BenzoElectric en el terreno 4. Diseño Conguración Descripción x x 1 Varilla 1.8[m] T4.1G GEM BenzoElectric x x x 2 Varillas 1.8[m] x T4.2G d=3[m] x GEM BenzoElectric x x x 3 Varillas 1.8[m] T4.3G d=3[m] x GEM BenzoElectric x Tabla 2.42: Implementación del GEM BenzoElectric en el terreno 4. En la Tabla 2.4.2.2 se observa la implementación del GEM BenzoElectric en el terreno 11. 60 Diseño Conguración Descripción x x 1 Varilla 1.8[m] T11.1G GEM BenzoElectric x x x 2 Varillas 1.8[m] x T11.2G d=3[m] x GEM BenzoElectric x x x 2 Varillas 1.8[m] T11.3G d=4[m] x GEM BenzoElectric x x x 2 Varillas 1.8[m] T11.4G d=5[m] x GEM BenzoElectric x x x 3 Varillas 1.8[m] T11.5G d=3[m] x GEM BenzoElectric x x x 3 Varillas 1.8[m] T11.6G d=4[m] x GEM BenzoElectric x x x 3 Varillas 1.8[m] T11.7G d=3[m] x GEM BenzoElectric x x 3 Varillas 1.8[m] x T11.8G d=4[m] x GEM BenzoElectric x Tabla 2.43: Implementación del GEM BenzoElectric en el terreno 11. En la Tabla 2.4.2.2 se observa la implementación del GEM BenzoElectric en el terreno 12. Diseño Conguración Descripción x x 1 Varilla 1.8[m] T12.1G GEM BenzoElectric x x Tabla 2.44: Implementación del GEM BenzoElectric en el terreno 12. 61 En la Tabla 2.4.2.2 se observa la implementación del GEM BenzoElectric en el terreno 13. Diseño Conguración Descripción x x 1 Varilla 1.8[m] T13.1G GEM BenzoElectric x x x x 2 Varillas 1.8[m] T13.2G d=3[m] x GEM BenzoElectric x x x 3 Varillas 1.8[m] T13.3G d=3[m] x GEM BenzoElectric x x x 3 Varillas 1.8[m] T13.4G d=3[m] x GEM BenzoElectric x x x 3 Varillas 1.8[m] T13.5G d=5[m] x GEM BenzoElectric x x 4 Varillas 1.8[m] x T13.6G d=3[m] x GEM BenzoElectric x Tabla 2.45: Implementación del GEM BenzoElectric en el terreno 13. En la Tabla 2.4.2.2 se observa la implementación del GEM BenzoElectric en el terreno 16. Diseño Conguración Descripción x x 1 Varilla 1.8[m] T16.2G GEM BenzoElectric x x x x 1 Varilla 2.4[m] T16.7G GEM BenzoElectric x x Tabla 2.46: Implementación del GEM BenzoElectric en el terreno 16. 62 2.4.3. Electrodo del tipo Químico En este trabajo se utiliza un electrodo químico de marca Parres EP-ET que se muestra en la Figura 2.4.3. Las principales características son: a) Por sus dimensiones y desempeño es de gran utilidad cuando se quiere obtener valores bajos de resistencia en el terreno de cortas dimensiones con valores medios y altos de resistividad. b) Disminuye la resistencia de contacto de puesta a tierra entre el cobre y el terreno, facilitando así el paso de la corriente. c) Su instalación es muy sencilla y elimina el tener que hacer grandes inversiones en obra civil y aplicación de múltiples elementos para la conformación de malla a tierras d) Tiene una longitud de 1m, diámetro externo de 0.16m, serpentín de cobre con cable de conexión # 2/0 AWG THW con una longitud de 0.5m. Figura 2.4.4: Electrodo Químico de puesta a tierra marca Parres. 2.4.3.1. Método de instalación En la Figura B (ANEXO B) se observa detalladamente la instalación del electrodo químico. Además, se usa Agregado Electrolitico EP-AE Parres de 1 galón (4 litros) como material complementario que se muestra en la Figura 2.4.3.1 . Este agregado se usa para reducir la resistencia de los electrodos de puesta a tierra, trabaja conjuntamente con el electrodo, aumentando su volumen de disipación e integrándolo parcialmente al terreno mismo. Una vez instalado el electrodo químico se vierte el EP-AE al centro del electrodo y se agrega pausadamente media cubeta de agua (8 litros) esperando a que sea absorbida totalmente. 63 Figura 2.4.5: Agregado Electrolítico para electrodos de puesta a tierra. 2.4.3.2. Implementación del Electrodo Químico En la Tabla 2.4.3.2 se observa la implementación del Electrodo Químico Parres en el terreno 16. Diseño Conguración Descripción x x 1 Electrodo T16.8 Químico 1[m] x x Tabla 2.47: Implementación del Electrodo Químico en el terreno 16. 2.5. Medición de la resistencia de puesta a tierra La medición de los sistemas de puesta a tierra se realizan mediante los métodos de caída de potencial y el método clamp-on descritos en los incisos 1.5.2.3 y 1.5.2.4 respectivamente. Adicionalmente, se realizan las mediciones de resistencia mediante el método de dos puntos descritos en el inciso 1.5.2.1 en algunos diseños implementados. Para el método de caída de potencial y el método de dos puntos se usa el telurómetro digital mostrado en la Figura 2.1.1, mientras que para el método de clamp-on se usa el medidor de resistencia tierra tipo pinza que se muestra en la Figura 2.5. Esta pinza de marca HT modelo T2000, es una abrazadera profesional especialmente desarrollada para medir la resistencia de varillas de tierra sin necesidad de desconectar parte del sistema. La parte interna del instrumento está compuesta por dos torioidales, uno de lectura de corriente y el otro es un generador de tensión. El toroidal de tensión genera un potencial sobre el anillo en la medida (de la resistencia R). Una corriente en consecuencia se genera sobre el anillo y es medida por el toroidal de corriente. Basándose en la relación E/I, el instrumento muestra en el visualizador el valor de la resistencia R calculada [7]. 64 Figura 2.5.1: Medidor de resistencia a tierra tipo Pinza. 2.5.1. Resultados de las mediciones Mediante la medición de la resistencia de puesta a tierra ya sea por el método de dos puntos y o por el método de clamp-on, se obtiene un solo valor de resistencia, mientras que para el método de la caída de potencial se puede obtener varias lecturas mediante la reubicación de las picas de tensión y corriente. Por ello, en (ANEXO D) se muestran los resultados obtenidos mediante el método de caída de potencial, mediante tres ubicaciones de las picas de corriente y voltaje. En las siguientes tablas se muestra las mediciones de resistencia de los diferentes sistemas de puesta a tierra implementados en cada terreno. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos del diseño implementado en el terreno 1 que tiene una resistividad aparente de 13 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] T1.1 6.67 7.22 Ω · m. Resistencia medida (Pinza) [Ω · m] 8.80 Tabla 2.48: Mediciones de la resistencia del diseño implementado en el terreno 1. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 2 que tiene una resistividad aparente de 18 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Ω · m. Resistencia medida (Pinza) [Ω · m] T2.1 9.23 6.95 7.10 T2.1G NA 4.35 5.10 T2.2 3.57 3.43 3.50 T2.2G NA 2.46 3.10 T2.3 1.91 1.90 2.4 Tabla 2.49: Mediciones de la resistencia de los diseños implementados en el terreno 2. NA: El diseño involucra GEM; no es calculado, solamente es medido. 65 En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos del diseño implementado en el terreno 3 que tiene una resistividad aparente de 24 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] T3.1 9.69 10.04 Ω · m. Resistencia medida (Pinza) [Ω · m] 10.10 Tabla 2.50: Mediciones de la resistencia de los diseños implementados en el terreno 3. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 4 que tiene una resistividad aparente de 28 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Resistencia medida (Pinza) [Ω · m] 14.37 13.98 T4.1G NA 7.94 9.30 T4.2 7.84 7.21 10.50 T4.2G NA 4.60 6.00 T4.3 5.37 5.35 8.90 T4.3G NA 3.69 5.60 T4.1 Ω · m. 15.50 Tabla 2.51: Mediciones de la resistencia de los diseños implementados en el terreno 4. NA: El diseño involucra GEM; no es calculado, solamente es medido. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos del diseño implementado en el terreno 5 que tiene una resistividad aparente de 30 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] T5.1 15.39 13.20 Ω · m. Resistencia medida (Pinza) [Ω · m] 12.70 Tabla 2.52: Mediciones de la resistencia del diseño implementado en el terreno 5. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos del diseño implementado en el terreno 6 que tiene una resistividad aparente de 32 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] T6.1 12.92 10.20 Ω · m. Resistencia medida (Pinza) [Ω · m] 10.60 Tabla 2.53: Mediciones de la resistencia del diseño implementado en el terreno 6. 66 En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos del diseño implementado en el terreno 7 que tiene una resistividad aparente de 35 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] T7.1 14.14 10.55 Ω · m. Resistencia medida (Pinza) [Ω · m] 11.20 Tabla 2.54: Mediciones de la resistencia de los diseños implementados en el terreno 7. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 8 que tiene una resistividad aparente de 45 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Ω · m. Resistencia medida (Pinza) [Ω · m] T8.1 23.09 21.80 22.00 T8.1G NA 13.84 14.40 T8.2 12.60 9.82 10.40 T8.2G NA 7.03 7.30 T8.3 18.17 16.81 16.70 T8.4 10.58 8.40 8.80 T8.5 7.51 6.28 6.40 Tabla 2.55: Mediciones de la resistencia de los diseños implementados en el terreno 8. NA: El diseño involucra GEM; no es calculado, solamente es medido. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 9 que tiene una resistividad aparente de 54 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Ω · m. Resistencia medida (Pinza) [Ω · m] T9.1 27.70 26.37 24.50 T9.2 13.76 12.04 11.90 Tabla 2.56: Mediciones de la resistencia de los diseños implementados en el terreno 9. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 10 que tiene una resistividad aparente de 63 67 Ω · m. Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Resistencia medida (Pinza) [Ω · m] T10.1 32.32 28.03 28.90 T10.2 17.64 15.88 15.60 T10.3 16.05 14.42 14.50 T10.4 14.69 12.11 12.50 Tabla 2.57: Mediciones de la resistencia de los diseños implementados en el terreno 10. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 11 que tiene una resistividad aparente de 91 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Resistencia medida (Pinza) [Ω · m] 46.69 43.40 44.50 T11.1G NA 26.47 26.70 T11.2 25.48 20.43 19.70 T11.2G NA 14.62 15.20 T11.3 23.19 19.64 19.30 T11.3G NA 14.34 14.70 T11.4 21.22 18.47 18.10 T11.4G NA 13.62 14.10 T11.5 17.46 13.64 14.40 T11.5G NA 9.96 10.80 T11.1 Ω · m. T11.6 15.24 12.95 13.80 T11.6G NA 9.78 10.50 T11.7 15.88 13.96 15.30 T11.7G NA 9.70 10.70 T11.8 13.45 12.24 12.80 T11.8G NA 9.40 10.30 Tabla 2.58: Mediciones de la resistencia de los diseños implementados en el terreno 11. NA: El diseño involucra GEM; no es calculado, solamente es medido. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 12 que tiene una resistividad aparente de 100 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Ω · m. Resistencia medida (Pinza) [Ω · m] T12.1 51.30 48.03 47.40 T12.1G NA 30.30 27.90 T12.2 25.48 21.50 21.00 T12.3 16.75 15.52 15.50 T12.4 14.78 12.64 12.40 Tabla 2.59: Mediciones de la resistencia de los diseños implementados en el terreno 12. NA: El diseño involucra GEM; no es calculado, solamente es medido. 68 En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 13 que tiene una resistividad aparente de 109 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Ω · m. Resistencia medida (Pinza) [Ω · m] T13.1 55.92 47.63 46.90 T13.1G NA 28.13 28.60 T13.2 30.52 27.90 27.70 T13.2G NA 14.91 15.80 T13.3 20.92 19.74 19.50 T13.3G NA 11.14 12.00 T13.4 19.02 16.59 17.00 T13.4G NA 10.57 11.60 T13.5 13.95 12.87 12.70 T13.5G NA 9.58 10.60 T13.6 13.74 12.96 13.10 T13.6G NA 9.41 9.40 T13.7 44.02 49.13 47.40 T13.8 23.64 20.05 19.30 T13.9 16.14 15.50 14.40 T13.10 14.64 12.73 12.70 Tabla 2.60: Mediciones de la resistencia de los diseños implementados en el terreno 13. NA: El diseño involucra GEM; no es calculado, solamente es medido. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 14 que tiene una resistividad aparente de 113 69 Ω · m. Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Resistencia medida (Pinza) [Ω · m] 57.97 57.40 53.50 T14.1G NA 24.53 23.10 T14.2 31.64 23.77 21.70 T14.2G NA 16.18 15.50 T14.3 28.79 23.63 21.20 T14.3G NA 15.60 14.90 T14.4 24.22 22.58 20.90 T14.4G NA 13.94 13.30 T14.5 21.69 17.65 16.20 T14.5G NA 10.89 10.80 T14.1 T14.6 16.79 15.98 14.70 T14.6G NA 9.80 10.40 T14.7 19.72 16.24 15.50 T14.7G NA 9.95 10.60 T14.8 14.46 14.03 14.60 T14.8G NA 8.41 9.30 T14.9 14.24 12.00 15.00 T14.9G NA 8.64 9.60 Tabla 2.61: Mediciones de la resistencia de los diseños implementados en el terreno 14. NA: El diseño involucra GEM; no es calculado, solamente es medido. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 15 que tiene una resistividad aparente de 169 Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída de potencial) [Ω · m] Ω · m. Resistencia medida (Pinza) [Ω · m] T15.1 86.70 70.63 65.00 T15.2 43.06 34.57 32.90 T15.2G NA 19.96 17.40 T15.3 68.25 64.80 62.00 T15.4 34.12 32.33 32.00 T15.5 22.56 19.37 19.00 T15.6 20.01 17.45 17.00 T15.7 14.38 13.49 13.20 Tabla 2.62: Mediciones de la resistencia de los diseños implementados en el terreno 15. NA: El diseño involucra GEM; no es calculado, solamente es medido. En la Tabla 2.5.1 se observa los valores de resistencia de puesta a tierra calculados y medidos para los diseños implementados en el terreno 16 que tiene una resistividad aparente de 181 70 Ω · m. Resistencia medida Resistencia Diseño calculada (Método de caída [Ω · m] Resistencia medida (Pinza) de potencial) [Ω · m] [Ω · m] T16.1 150.22 143.57 142.00 T16.2 92.86 92.97 89.00 T16.2G NA 41.47 38.80 T16.3 38.80 36.23 33.10 T16.4 24.16 23.47 21.50 T16.5 20.42 18.37 17.20 T16.6 14.59 13.63 13.20 T16.7 73.10 71.27 64.50 T16.7G NA 35.50 35.00 T16.8 NA 39.20 41.40 Tabla 2.63: Mediciones de la resistencia de los diseños implementados en el terreno 16. NA: El diseño involucra GEM; no es calculado, solamente es medido. Adicionalmente, se realizó la medida de la resistencia de puesta a tierra mediante el método de dos puntos en una muestra de todas las conguraciones, en la Tabla 2.5.1 se puede observar los resultados y las comparaciones que se realiza con los resultados obtenidos de los dos métodos anteriormente mencionados. Resistencia medida Diseño Resistencia calculada [Ω · m] (Método de caída Resistencia medida de potencial) [Ω · m] (Pinza) [Ω · m] Resistencia medida (Método de dos puntos) [Ω · m] T6.1 12.92 10.20 10.60 9.97 T8.5 7.51 6.28 6.40 6.41 T11.7 15.88 13.96 15.30 14.00 T14.9 14.24 12.00 15.00 12.76 T4.3G NA 3.69 5.60 3.76 T12.1G NA 30.30 27.90 32.50 T13.6G NA 9.41 9.40 9.74 T15.2G NA 19.96 17.40 21.70 Tabla 2.64: Mediciones de resistencia de puesta a tierra mediante 3 métodos. NA: El diseño involucra GEM; no es calculado, solamente es medido. 71 Capítulo 3 ANÁLISIS DE LOS RESULTADOS 3.1. Resultados de las tensiones tolerables Los resultados de las tensiones de paso y de contacto para el diseño T2.3 se presentan en la Tabla 3.1 Como se puede observar ha cumplido con los requerimientos de tensiones tolerables según la norma IEEE Std 80-2013. Valores Denominación Calculados #2 AWG Conductor Resistencia del sistema de puesta a tierra Epaso tolerable Econtacto Tensión de paso tolerable Tensión de contacto Potencial máximo de la malla GPR Tensión de paso real Es Es Tensión de contacto real 1.91 Ω 2985.73 V 912.96 1959.66 V 681.67 V 526.59 V Tabla 3.1: Resultados de las tensiones tolerables del diseño T2.3 Si bien los sistemas de puesta a tierra pueden ajustarse para eliminar los potenciales de contacto peligrosos mediante la supresión de las corrientes de cortocircuito a tierra, esto no suele exigirse a los sistemas con neutros conectados a tierra con corrientes de falla menores a 1000A, porque no parece viable. Para corrientes de falla a tierra por encima de 1000 A, se deben instalar sistemas de puesta a tierra de grandes dimensiones para cumplir con los usuales requisitos de potenciales de paso y de contacto [8]. 3.2. Resultados de la formulación utilizada Las mediciones obtenidas mediante el método de caída de potencial, comparadas con los cálculos resultan similares. Los valores medidos son menores a los calculados siendo muy benecioso ya que se tiene un margen de error. Siendo así que la ecuación de Dwight, las ecuaciones de Schwarz y las ecuaciones realizadas para este proyecto son validadas, y se pueden utilizar en la práctica. En las siguientes tablas se presenta un resumen de los cálculos y mediciones realizados para los distintos diseños. En la Tabla 3.2, se dan a conocer los resultados de la medición de la resistencia de una varilla mediante el método de caída de potencial. 72 Diseño Resistividad [Ω · m] Longitud de la varilla [m] Resistencia Resistencia calculada medida [Ω] [Ω] 7.22 T1.1 13 1.8[m] 6.67 T2.1 18 1.8[m] 9.23 6.95 T3.1 24 2.4[m] 9.69 10.04 T4.1 28 1.8[m] 14.37 13.98 T5.1 30 1.8[m] 15.39 13.20 T6.1 32 2.4[m] 12.92 10.20 T7.1 35 2.4[m] 14.14 10.55 T8.1 45 1.8[m] 23.09 21.80 T8.3 45 2.4[m] 18.17 16.81 T9.1 54 1.8[m] 27.70 26.37 T10.1 63 1.8[m] 32.32 28.03 T11.1 91 1.8[m] 46.69 43.40 T12.1 100 1.8[m] 51.30 48.03 T13.1 109 1.8[m] 55.92 47.63 T13.7 109 2.4[m] 44.02 49.13 T14.1 113 1.8[m] 57.98 57.40 T15.1 169 1.8[m] 86.70 70.63 T15.3 169 2.4[m] 68.25 64.80 T16.1 181 1.0[m] 150.22 143.57 T16.2 181 1.8[m] 92.86 92.97 T16.7 181 2.4[m] 73.10 71.27 Tabla 3.2: Cálculos y mediciones para el diseño de una varilla. Los valores medidos para una varilla presentan un error promedio de 2.70 ohmios por debajo de la resistencia calculada. En la Tabla 3.2, se dan a conocer los resultados de la medición de la resistencia de dos varillas en línea separadas a una distancia ”d”, con el conductor enterrado a una profundidad 73 h = 0,25m. Diseño Resistividad [Ω · m] Longitud de la varilla Distancia de [m] separación ”d” Resistencia Resistencia calculada medida [m] [Ω] [Ω] 3.57 3.43 T2.2 18 1.8[m] 7[m] T4.2 28 1.8[m] 3[m] 7.84 7.21 T8.2 45 1.8[m] 3[m] 12.60 9.82 T8.4 45 2.4[m] 3[m] 10.56 8.40 T9.2 54 1.8[m] 4[m] 13.76 12.04 T10.2 63 1.8[m] 3[m] 17.64 15.88 T10.3 63 1.8[m] 4[m] 16.05 14.42 T10.4 63 1.8[m] 5[m] 14.69 12.11 T11.2 91 1.8[m] 3[m] 25.48 20.43 T11.3 91 1.8[m] 4[m] 23.19 19.64 T11.4 91 1.8[m] 5[m] 21.22 18.47 T12.2 100 1.8[m] 4[m] 25.48 21.50 T13.2 109 1.8[m] 3[m] 30.52 27.90 T13.8 109 2.4[m] 4[m] 23.64 20.05 T14.2 113 1.8[m] 3[m] 31.64 23.77 T14.3 113 1.8[m] 4[m] 28.79 23.63 T14.4 113 1.8[m] 6[m] 24.22 22.58 T15.2 169 1.8[m] 4[m] 43.06 34.57 T15.4 169 2.4[m] 5[m] 34.12 32.33 T16.3 181 1.8[m] 6[m] 38.80 36.23 Tabla 3.3: Cálculos y mediciones para el diseño de dos varillas. Los valores medidos para la unión de dos varillas presentan un error promedio de 2.62 ohmios por debajo de la resistencia calculada. En la Tabla 3.2, se dan a conocer los resultados de la medición de la resistencia de tres varillas en línea separadas a una distancia Diseño Resistividad [Ω · m] ”d” entre las varillas adyacentes. Longitud de la varilla Distancia de [m] Resistencia Resistencia calculada medida [m] [Ω] [Ω] 5.35 separación ”d” T4.3 28 1.8[m] 3[m] 5.37 T8.5 45 2.4[m] 3[m] 7.51 6.28 T11.5 91 1.8[m] 3[m] 17.46 13.64 T11.6 91 1.8[m] 4[m] 15.24 12.95 T12.3 100 1.8[m] 4[m] 16.75 15.52 T13.3 109 1.8[m] 3[m] 20.92 19.74 T13.9 109 2.4[m] 4[m] 16.14 15.50 T14.5 113 1.8[m] 3[m] 21.69 17.65 T14.6 113 1.8[m] 5[m] 16.79 15.98 T15.5 169 2.4[m] 5[m] 22.56 19.37 T16.4 181 1.8[m] 6[m] 24.16 23.47 Tabla 3.4: Cálculos y mediciones para el diseño de tres varillas en disposición lineal. Los valores medidos para la unión de tres varillas en línea presentan un error promedio de 1.74 ohmios por debajo de la resistencia calculada. En la Tabla 3.2, se dan a conocer los resultados de la medición de la resistencia de tres varillas en triángulo separadas a una distancia ”d” en cada uno de sus lados. 74 Diseño Resistividad [Ω · m] T11.7 Longitud de la varilla [m] Distancia de separación ”d” Resistencia Resistencia calculada medida [m] [Ω] [Ω] 91 1.8[m] 3[m] 15.88 13.96 T11.8 91 1.8[m] 4[m] 13.45 12.24 T12.4 100 1.8[m] 4[m] 14.78 12.64 T13.4 109 1.8[m] 3[m] 19.02 16.59 T13.5 109 1.8[m] 5[m] 13.95 12.87 T13.10 109 2.4[m] 4[m] 14.64 12.73 T14.7 113 1.8[m] 3[m] 19.72 16.24 T14.8 113 1.8[m] 5[m] 14.46 14.03 T15.6 169 2.4[m] 5[m] 20.01 17.45 T16.5 181 1.8[m] 6[m] 20.42 18.37 Tabla 3.5: Cálculos y mediciones para el diseño de tres varillas en disposición triangular. Los valores medidos para la unión de tres varillas en triángulo presentan un error promedio de 1.92 ohmios por debajo de la resistencia calculada. En la Tabla 3.2, se dan a conocer los resultados de la medición de la resistencia las mallas cuadradas implementadas, siendo Diseño Resistividad [Ω · m] ”d” la distancia de cada uno de sus lados. Longitud de la varilla [m] Distancia de separación ”d” [m] Resistencia Resistencia calculada medida [Ω] [Ω] T2.3 18 1.8[m] 4[m] 1.91 1.9 T13.6 109 1.8[m] 3[m] 13.74 12.96 T14.9 113 1.8[m] 3[m] 14.24 12 T15.7 169 2.4[m] 5[m] 14.38 13.49 T16.6 181 1.8[m] 6[m] 14.59 13.63 Tabla 3.6: Cálculos y mediciones para el diseño de mallas cuadradas. Los valores medidos para la malla cuadra con cuatro varillas presentan un error promedio de 0.98 ohmios por debajo de la resistencia calculada. 3.3. Resultados de la adherencia del GEM con el terreno y las varillas Después de la aplicación del mejorador de tierra GEM, se obtuvo una evidente disminución en la resistencia de puesta a tierra. Así mismo, en el lapso de 30 días se tomaron nuevas lecturas de la resistencia de puesta a tierra tanto para la aplicación del GEM Cadweld como para el GEM BenzoElectric, resultando en una pequeña disminución de la resistencia a la medida inicial (3 días después de la implementación). Sin embargo, se ha notado que el GEM BenzoElectric no tuvo un buen desarrollo en cuanto a la compactación con el electrodo y el terreno, ya que se encontraba en un estado viscoso como se puede apreciar en la Figura 3.3 (a). Por otro lado, el GEM Cadweld tuvo excelentes resultados en este factor ya que se adhirió al electrodo uniformemente, para observar su efecto se sacó la varilla cuidadosamente. En la Figura 3.3 (b) se puede observar el GEM Cadweld adherido a la varilla. 75 Figura 3.3.1: Compactibilidad: a) GEM premezclado y b) GEM en polvo 3.4. Resultados de la aplicación del GEM Cadweld El valor porcentual de la reducción de la resistencia de puesta a tierra, implementando GEM Cadweld se observa en la Tabla 3.4. La resistencia es medida mediante el método de caída de potencial. Diseño Resistencia Resistencia calculada con medida varillas y solamente con conductor T8.1G 23.09 [Ω] varillas [Ω] Resistencia Reducción del medida GEM con GEM con después de la respecto al respecto a la aplicación del cálculo medición [ %] [ %] 13.84 40 % 37 % GEM 21.80 [Ω] Reducción del T8.2G 12.60 9.82 7.03 44 % 28 % T14.1G 57.97 57.40 24.53 58 % 57 % T14.2G 31.64 23.77 16.18 49 % 32 % T14.3G 28.79 23.63 15.60 46 % 34 % T14.4G 24.22 22.58 13.94 42 % 38 % T14.5G 21.69 17.65 10.89 50 % 38 % T14.6G 16.79 15.98 9.80 42 % 39 % T14.7G 19.72 16.24 9.95 50 % 39 % T14.8G 14.46 14.03 8.41 42 % 40 % T14.9G 14.24 12.00 8.64 39 % 28 % T15.2G 43.06 34.57 19.96 54 % 42 % Tabla 3.7: Resultados mediante la aplicación del GEM Cadweld 76 Se puede observar que la reducción de la resistencia de puesta a tierra con respecto al valor calculado solamente usando varillas y conductores tiene un promedio de 46 %, mientras que la reducción de la resistencia de puesta a tierra del sistema con GEM con respecto al mismo sistema medido usando solo varillas tiene un promedio de 38 %. Teniendo en cuenta un rango de seguridad se determina que la disminución de la resistencia de puesta a tierra usando GEM Cadweld con respecto al diseño básico calculado es de 40 %, y con respecto al diseño básico medido es del 35 %. 3.5. Resultados de la aplicación del GEM BenzoElectric El valor porcentual de la reducción de la resistencia de puesta a tierra, implementando GEM Cadweld se observa en la Tabla 3.5. La resistencia es medida mediante el método de caída de potencial. Diseño Resistencia Resistencia calculada con medida varillas y solamente con conductor [Ω] varillas [Ω] Resistencia Reducción del medida GEM con GEM con después de la respecto al respecto a la aplicación del cálculo medición [ %] [ %] GEM [Ω] Reducción del T2.1G 9.23 6.95 4.35 53 % 37 % T2.2G 3.57 3.43 2.46 31 % 28 % T4.1G 14.37 13.98 7.94 45 % 43 % T4.2G 7.84 7.21 4.60 41 % 36 % T4.3G 5.37 5.35 3.69 31 % 31 % T11.1G 46.69 43.40 26.47 43 % 39 % T11.2G 25.48 20.43 14.62 43 % 28 % T11.3G 23.19 19.64 14.34 38 % 27 % T11.4G 21.22 18.47 13.62 36 % 26 % T11.5G 17.46 13.64 9.96 43 % 27 % T11.6G 15.24 12.95 9.78 36 % 25 % T11.7G 15.88 13.96 9.70 39 % 31 % T11.8G 13.45 12.24 9.40 30 % 23 % T12.1G 51.30 48.03 30.30 41 % 37 % T13.1G 55.92 47.63 28.13 50 % 41 % T13.2G 30.52 27.90 14.91 51 % 47 % T13.3G 20.92 19.74 11.14 47 % 44 % T13.4G 19.02 16.59 10.57 44 % 36 % T13.5G 13.95 12.87 9.58 31 % 26 % T13.6G 13.74 12.96 9.41 32 % 27 % T16.2G 92.86 92.97 41.47 55 % 55 % T16.7G 73.10 71.27 35.50 51 % 50 % Tabla 3.8: Resultados mediante la aplicación del GEM BenzoElectric El promedio de la reducción de la resistencia de puesta a tierra con respecto al valor calculado solamente usando varillas y conductores es de 41 %, mientras que el promedio de la reducción de la resistencia de puesta a tierra del sistema con GEM con respecto al mismo sistema medido solamente con varillas y conductor es de 35 %. Teniendo en cuenta un rango de seguridad se determina que la disminución de la resistencia de puesta a tierra usando GEM BenzoElectric con respecto al diseño básico calculado y medido es del 30 %. 3.6. Resultados de la aplicación del Electrodo Químico Para conocer si la implementación de un electrodo químico es conveniente, en la Tabla 3.6 se puede comparar la resistencia de puesta a tierra medida (por el método de caída de potencial) del 77 electrodo químico con la de algunos diseños que se implementaron en el mismo terreno. Resistencia Diseño Descripción T16.1 1 Varilla 1[m] 143.57 T16.2 1 Varilla 1.8[m] 92.97 T16.2G 1 Varilla 1.8[m] 41.47 Medida [Ω] GEM BenzoElectric T16.3 2 Varillas 1.8[m] d=6[m] 36.23 T16.4 3 Varillas 1.8[m] 23.47 En línea d=6[m] T16.5 3 Varillas 1.8[m] 18.37 En triángulo d=6[m] T16.6 4 Varillas 1.8[m] 13.63 En cuadrado d=6[m] T16.7 1 Varilla 2.4[m] 71.27 T16.7G 1 Varilla 2.4[m] 35.50 T16.8 1 Electrodo Químico 1[m] x GEM BenzoElectric 39.20 Tabla 3.9: Diseños de sistemas de puesta a tierra para el terreno 16. Como se puede observar existen varias maneras de obtener una resistencia similar al obtenido por el electrodo químico, sin embargo, el electrodo químico cuenta con la ventaja de que tiene una pequeña longitud de 1m, para aplicaciones en donde no se puede implementar otro sistema. 3.7. Implementaciones para una resistencia de puesta a tierra de 15 ohmios Los diseños utilizados para obtener la resistencia de puesta a tierra de 15 ohmios, usando varillas de cobre 1.8m x 5/8 se presentan en la Tabla 3.7. 78 Resistividad Diseño aparente Descripción [Ω · m] Resistencia de Resistencia de puesta a puesta a tierra tierra calculada[Ω] medida[Ω] 6.67 7.22 T1.1 13 1 Varilla 1.8[m] T2.1 18 1 Varilla 1.8[m] 9.23 6.95 T4.1 28 1 Varilla 1.8[m] 14.37 13.98 T8.2 45 12.60 9.82 T9.2 54 13.76 12.04 T10.4 63 14.69 12.11 T11.8 91 13.45 12.24 14.78 12.64 13.95 12.87 13.74 12.96 14.46 14.03 14.24 12.00 14.59 13.63 2 Varillas 1.8[m] d=3[m] 2 Varillas 1.8[m] d=4[m] 2 Varillas 1.8[m] d=5[m] 3 Varillas 1.8[m] Triángulo d=4[m] 3 Varillas 1.8[m] T12.4 100 Triángulo d=4[m] 3 Varillas 1.8[m] T13.5 109 Triángulo d=5[m] 4 Varillas 1.8[m] T13.6 109 Cuadrado d=3[m] 3 Varillas 1.8[m] T14.8 113 Triángulo d=5[m] 4 Varillas 1.8[m] T14.9 113 Cuadrado d=3[m] 4 Varillas 1.8[m] T16.6 181 Cuadrado d=6[m] Tabla 3.10: Diseños implementados con varillas de 1.8m para una resistencia objetivo de 15 ohmios. Los diseños implementados para obtener una resistencia de tierra inferior o igual a 15 ohmios, usando varillas de cobre 2.4m x 5/8 se presentan en la Tabla 3.7. 79 Resistividad Diseño aparente Resistencia de Resistencia de puesta a puesta a Descripción [Ω · m] tierra tierra calculada[Ω] medida[Ω] T3.1 24 1 Varilla 2.4[m] 9.69 10.04 T6.1 32 1 Varilla 2.4[m] 12.92 10.20 T7.1 35 1 Varilla 2.4[m] 14.14 10.55 10.56 8.40 14.64 12.73 14.38 13.49 T8.4 45 T13.10 109 2 Varillas 2.4[m] d=3[m] 3 Varillas 2.4[m] Triángulo d=4[m] 4 Varillas 2.4[m] T15.7 169 Cuadrado d=5[m] Tabla 3.11: Diseños implementados con varillas de 2.7m para una resistencia objetivo de aproximadamente 15 ohmios. También se ha podido obtener valores aproximados a la resistencia de 15 ohmios mediante la aplicación de GEM Cadweld como se puede ver en la Tabla 3.7. Resistencia de Resistividad Diseño aparente Descripción [Ω · m] T8.1G 45 T14.4G 113 puesta a tierra medida[Ω] 1 Varilla 1.8[m] GEM Cadweld 13.84 2 Varillas 1.8[m] d=6[m] 13.94 GEM Cadweld Tabla 3.12: Diseños implementados con GEM Cadweld obteniendo una resistencia inferior a 15 ohmios. De igual manera se han implementado diseños para tener una resistencia inferior o igual a 15 ohmios mediante la aplicación de GEM BenzoElectric como se puede ver en la Tabla 3.7. Observándose que en los dos primeros diseños se tiene una resistencia muy pequeña, en tal caso es recomendable una varilla sin tratamiento. 80 Resistencia de Resistividad Diseño aparente Descripción [Ω · m] puesta a tierra medida[Ω] 1 Varilla 1.8[m] T2.1G 18 GEM 4.35 BenzoElectric 1 Varilla 1.8[m] T4.1G 28 GEM 7.94 BenzoElectric 2 Varillas 1.8[m] T11.4G d=5[m] 91 GEM 13.62 BenzoElectric 3 Varillas 1.8[m] En línea T13.3G 109 d=3[m] 11.14 GEM BenzoElectric Tabla 3.13: Diseños implementados con GEM BenzoElectric para una resistencia objetivo. 81 Capítulo 4 CONCLUSIONES Y RECOMENDACIONES 4.1. CONCLUSIONES En base a las implementaciones de campo, mediciones e interpretaciones de los resultados que se realizaron en este proyecto se pueden listar las siguientes conclusiones: Las mediciones de la resistividad mediante el método de cuatro picas arreglo Wenner realizadas en 4 direcciones y a 1m, 2m, 3m de separación de las picas, fueron sucientes para realizar un modelamiento de terreno uniforme en los 15 primeros terrenos, mientras que para el terreno 16 se obtuvo la resistividad aparente mediante el método gráco de Sunde. Así mismo, los modelos utilizados tanto para un terreno uniforme como para el método gráco Sunde fueron los adecuados ya que posteriormente se comprobó con la implementación de varios diseños. En el diseño T2.3 se cumplió con los requisitos de tensiones tolerables de acuerdo a la norma IEEE Std 80-2013. Así mismo, es importante mencionar que en los sistemas de puestas a tierra con una corriente de falla superior a 1000A es necesario realizar estos cálculos de tensiones de paso y de contacto, mientras que la misma norma IEEE Std 80-2013 señala que esto no suele exigirse a los sistemas con neutros conectados a tierra con corrientes de falla inferiores a 1000A, porque no parece viable. Por tal motivo, en este proyecto no se analizan las tensiones tolerables (excepto el diseño T2.3), ya que los diseños de puesta a tierra están dirigidos para aplicaciones donde existen niveles bajos de corrientes de falla a tierra. Para comprobar la formulación que se utiliza para el cálculo de la resistencia de puesta a tierra, se implementaron diseños con distintas conguraciones en cada uno de los terrenos con una resistencia objetivo de 15Ω. Teniendo como resultado una gran similitud entre el cálculo y las mediciones. Por lo general la resistencia medida tiene un promedio de 3 ohmios por debajo de la resistencia la calculada, dando así un margen de error muy conveniente en la práctica. Por lo que queda demostrado que las ecuaciones de Schwarz, Dwight y las ecuaciones incorporadas en este proyecto para calcular la resistencia de puesta a tierra, son aplicables en la práctica. Para las mediciones de resistencia mediante el método de dos puntos y el método de clamp-on, se utilizó como tierra auxiliar el neutro de las casas residenciales cercanas a los terrenos de prueba. Debido a que estas casas tienen una puesta a tierra de baja impedancia por su conexión con el conductor neutro del sistema de alimentación. Por otro lado, para medir la resistencia de tierra por el método de caída de potencial se usaron diferentes separaciones de las picas de corriente y voltaje 82 con respecto al electrodo bajo prueba, para eliminar la sospecha de que pueda existir interferencias de estructuras o circuitos cercanos, pudiendo ser una fuente que añada o reste la corriente a la pica de prueba inyectada, teniendo lecturas incorrectas. Los resultados obtenidos mediante los tres métodos son similares, teniendo un rango de error de ±3Ω con respecto a la resistencia medida por el método de caída de potencial que se considera el más conable. En muy pocos casos se observa que el margen de error es de ±5Ω. Siendo así que se puede concluir que los tres métodos proporcionan resultados similares, pero siempre considerando que el método más adecuado para medir la resistencia de tierra es el de caída de potencial. Mediante la implementación del GEM Cadweld se obtuvo una reducción de la resistencia alrededor del 40 % con respecto a la resistencia calculada solamente con varillas y conductores, mientras que comparada con la resistencia medida se tiene una reducción aproximadamente del 35 %. Por otro lado la reducción de la resistencia de tierra con la aplicación de GEM BenzoElectric está alrededor del 35 % con respecto a la resistencia calculada, mientras que se tiene una disminución en la resistencia del 30 % con respecto a la resistencia medida. Sin embargo, la compactación con el terreno y el electrodo no resulta de la misma manera, ya que usando GEM premezclado (BenzoElectric) en el lapso de tres meses desde su implementación no se observó la compactación del mismo con la tierra ni con el electrodo observándose una solución viscosa en el agujero, sin bien es cierto conservando el nivel de conductividad ya que la resistencia no disminuyó. Mientras que, el GEM implementado en seco (Cadweld) tuvo una compactación ideal adhiriéndose al electrodo de forma que se vuelve muy difícil el hurto del mismo. En la Figura 3.3 (b) se puede estimar el nivel de adherencia que ofrece. A pesar de que el GEM Cadweld tiene un costo de casi el doble del GEM BenzoElectric se concluye que la aplicación de GEM en polvo es la primera opción para un tratamiento del terreno. Los diseños con varillas y conductores solamente, son los más económicos para la implementación pero se puede considerar la utilización de estos mejoradores especialmente en terrenos donde no existan muchas rocas o grava que pueda dicultar la excavación del agujero. Aunque la implementación del electrodo químico resulte muy sencilla y se obtenga una baja resistencia de tierra, se ha determinado que no es conveniente su uso por su precio elevado de aproximadamente 20 veces que el mejorador de tierra premezclado (BenzoElectric) y 14 veces mayor que el mejorador de tierra en seco (Cadweld). En la Tabla ?? se ha demostrado que se puede obtener una resistencia a tierra similar usando GEM BenzoElectric en una sola varilla, o mediante dos varillas de 1.8m de longitud a una separación de 6m. Su uso podría ser justicado en situaciones donde no se cuente con espacio suciente para la implementación de varillas y conductores, así como tratamientos del terreno. 83 4.2. RECOMENDACIONES Para las mediciones de resistividad del suelo por el método de Wenner, se recomienda separar las picas a 1m, 2m, y 3m como mínimo. Además, para tener mediciones totalmente conables y descartar la presencia de elementos metálicos enterrados en el terreno es recomendable medir en 4 direcciones alrededor del punto medio del terreno como se muestra en la Figura 2.1.2. De igual manera los objetos enterrados alrededor de las picas pueden inuir en las mediciones de la resistencia de puesta a tierra mediante el método de caída de potencial, es por ello que se recomienda realizar tres mediciones variando las picas de corriente y de voltaje. Obteniéndose de esta manera resultados conables. Si se desea realizar un tratamiento del terreno para reducir la resistividad se recomienda usar un material en seco como el GEM Cadweld, ya que éste tiene una adherencia ideal con el electrodo y la tierra. Mientras que en el GEM premezclado no se notó una compactación en un lapso de tres meses, solo observándose una solución viscosa. En casos de ser necesario la instalación del GEM premezclado, se recomienda combinarlo con la tierra obtenida del agujero y proceder a rellenar el hoyo nuevamente, para tener un mayor grado de adherencia con el electrodo y el terreno. Para la aplicación del GEM en varillas verticales, en la práctica difícilmente se obtiene un agujero de la longitud de la varilla sobre todo si esta es de 2.4m. Por lo que se recomienda se realice un agujero de 1.10m ya que a mayores profundidades se ha notado la presencia de roca. Así mismo, se recomienda un diámetro del agujero de 20cm aproximadamente. En terrenos donde no haya la presencia de muchas rocas se puede realizar el agujero y colocar directamente el GEM, por lo contrario en terrenos rocosos de difícil excavación se recomienda el uso de un tubo de aproximadamente 20 cm de diámetro para colocarlo en el agujero y rellenar las partes externas apisonando bien la tierra para luego retirarlo y tener un diámetro del agujero deseado como se observa en la Figura 2.4.2.1. Finalmente, en base a numerosos cálculos y mediciones, para obtener una resistencia de puesta a tierra de 15Ω, en terrenos con resistividades entre 1Ω ·m y 250Ω · m, se recomienda usar los diseños indicados en la Tabla 4.2. Los diseños no involucran varillas de 2.4m de longitud ya que su implementación resulta ser muy complicada. En cuanto a la profundidad de enterramiento del conductor cabe mencionar que con su variación se tiene muy poca relación con los cambios en la resistencia de tierra. Así mismo la separación d entre varillas es de 3m como mínimo. 84 Diseños de Sistemas de Puesta a Tierra para una resistencia de 15Ω Varilla copperweld: 1.8m x 5/8 Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 1-29 x x x 30-53 d=3[m] x x 54-64 d=5[m] x x x 65-78 d=3[m] x xx x x 79-117 d=5[m] x x x x 118-141 d=4[m] 142-163 d=5[m] 164-186 d=6[m] x x x x 187-216 d=5[m] 217-248 d=6[m] 249-280 d=7[m] x x Tabla 4.1: Diseños recomendados para obtener una resistencia de 15 ohm usando conductor (horizontal) y varillas (vertical). Los diseños recomendados para obtener una resistencia de puesta a tierra de 15Ω, en terrenos con una resistividad entre 1Ω · m y 250Ω · m, usando GEM BenzoElectric se pueden observar en la Tabla 4.2 . Los rangos de resistividad, se obtienen disminuyendo el 30 % del diseño básico. 85 Diseños de Sistemas de Puesta a Tierra para una resistencia de 15Ω Varilla copperweld: 1.8m x 5/8 + GEM BenzoElectric Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 30-41 x x x 42-76 d=3[m] x x 77-91 d=5[m] x x x 92-111 d=3[m] x xx x x 112-168 d=5[m] x x x x 169-202 d=4[m] 203-234 d=5[m] 235-265 d=6[m] x x Tabla 4.2: Diseños recomendados para obtener una resistencia de 15 ohm usando GEM BenzoElectric. Los diseños recomendados para obtener una resistencia de puesta a tierra de 15Ω, en terrenos con una resistividad entre 1Ω · m y 250Ω · m, usando GEM Cadweld se pueden observar en la Tabla 4.2 . Los rangos de resistividad, se obtienen disminuyendo el 40 % del diseño básico. 86 Diseños de Sistemas de Puesta a Tierra para una resistencia de 15Ω Varilla copperweld: 1.8m x 5/8 + GEM Cadweld Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 30-48 x x x 49-89 d=3[m] x x 90-107 d=5[m] x x x 108-130 d=3[m] x xx x x 131-195 d=5[m] x x x 196-236 x x d=4[m] x 237-273 d=5[m] x Tabla 4.3: Diseños recomendados para obtener una resistencia de 15 ohm usando GEM Cadweld. Las tablas con diseños de sistemas de puesta a tierra realizadas en este trabajo se basan en la combinación de numerosos cálculos y mediciones de campo, sin embargo, debe tenerse en cuenta que existen innumerables maneras de llegar a una resistencia deseada de puesta a tierra. En (ANEXO E) se puede observar conguraciones para obtener una resistencia de puesta a tierra de 10Ωy 20Ω mediante diseños básicos, GEM Cadweld y GEM BenzoElectric. 87 Bibliografía [1] ERICO GEM25A. GEM Material de Refuerzo de Tierra. Manual de usuario. [2] PARRES EP-ET. Electrodo Químico de Puesta a Tierra. Instrucciones. Disponible en: www.parres.com.mx. [3] IEEE Std 142-2007 (Revision of IEEE Std 142-1991). Power Systems, 2007. [4] AMPROBE. Grounding of Industrial and Commercial GP-2A, Earth Ground Tester. Users Manual, 2012. [5] Empresa Eléctrica Regional del Sur S.A. urbanas y rurales, page 35, Enero 2012. Normas técnicas para el diseño de redes eléctricas IEEE Guide for Measuring Earth Resistivity, Ground Impedance, and Earth Surface Potentials of a Grounding System, December [6] IEEE Std 81-2012 (Revision of IEEE Std 81-1983). 2012. [7] HT T2000-T2100. Manual de instrucciones, Octubre 2013. [8] IEEE Std 80-2013 (Revision of IEEE Std 80-2000/Incorporates IEEE Std 80-2013/Cor 12015). IEEE Guide for Safety in AC Substation Grounding, 2013. [9] NFPA 70. National Electrical Code (NEC), page Part 250.53, 2014. Diseño eléctrico de la subestación El Bosque de 20/24 MVA a 69KV con 4 circuitos de salida de 13,8KV en la ciudad de Machala, pages [10] Junior Aguilar. Universidad Politécnica Salesiana. 6284, Abril 2013. [11] Pablo Díaz. Soluciones prácticas para la puesta a tierra de sistemas eléctricos de distribución. Mexico, Febrero 2001. Normas técnicas para diseño y expansión de las redes secundarias del sistema de distribución de la Empresa Eléctrica Regional Centro Sur C.A., pages 9597, 2011. [12] Edwin Dominguez. Universidad de Cuenca. Diseño y construcción de puestas a tierra para el colegio técnico industrial Gualaceo, basado en las recomendaciones prácticas para el aterrizamiento en sistemas eléctricos comerciales e industriales de la IEEE, pages 116126, [13] Pablo Gómez. Universidad Politécnica Salesiana. 2010. [14] Jinliang He. Methodology and Technology for Power System Grounding. [15] Johny Montaña. Teoría de puestas a tierra. [16] Valencia J. Moreno G. fallas eléctricas y rayos. China, 2013. Bogotá - Colombia, ecoe edition, 2011. Fundamentos e ingeniería de las puestas a tierra. Respuestas ante Editorial Universidad de Antioquia, 2007. Universidad Politécnica Salesiana. Diseño de sistemas de puesta a tierra partiendo de un modelo biestraticado de terreno, aplicando un software computacional en el sector industrial, Marzo 2013. [17] Ángel Pacheco. Manual de aplicaciones de la norma IEEE Std 81 para líneas y subestaciones eléctricas de transmisión, Noviembre 2015. [18] Walter Pérez. Universidad de EL Salvador. 88 Anexo A MODELO DEL SUELO POR EL MÉTODO GRÁFICO SUNDE 89 Modelamiento para el terreno 1 a) En la Figura A.0.2 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 11,44Ω · m y ρa del terreno 1. ρ2 = 14,07Ω · m ρ2 /ρ1 = 1,23Ω · m ρa /ρ1 = 1,17, es seleccionado de la Figura A.0.1. a h = 3,4 Figura A.0.1: Gráca de Sunde del terreno 1. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 13,38Ω · m Se selecciona el valor de separación a = 2,71m 90 de la curva en la Figura A.0.2. Figura A.0.2: Curva de resistividad aparente del terreno 1. h) La profundidad del nivel superior (h) es h= a a h = 0,80m Modelamiento para el terreno 2 a) En la Figura A.0.4 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 17,92Ω · m y ρ2 = 17,06Ω · m ρ2 /ρ1 = 0,95Ω · m ρa /ρ1 = 0,97, es seleccionado de la Figura A.0.3. a h = 4,5 91 ρa del terreno 2. Figura A.0.3: Gráca de Sunde del terreno 2. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 17,38Ω · m Se selecciona el valor de separación a = 1,59m 92 de la curva en la Figura A.0.4. Figura A.0.4: Curva de resistividad aparente del terreno 2. h) La profundidad del nivel superior (h) es h= a a h = 0,35m Modelamiento para el terreno 3 a) En la Figura A.0.6 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 23,95Ω · m y ρ2 = 22,40Ω · m ρ2 /ρ1 = 0,94Ω · m ρa /ρ1 = 0,96, es seleccionado de la Figura A.0.5. a h = 4,4 93 ρa del terreno 3. Figura A.0.5: Gráca de Sunde del terreno 3. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 22,99Ω · m Se selecciona el valor de separación a = 2,06m 94 de la curva en la Figura A.0.6. Figura A.0.6: Curva de resistividad aparente del terreno 3. h) La profundidad del nivel superior (h) es h= a a h = 0,47m Modelamiento para el terreno 4 a) En la Figura A.0.8 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 25,53Ω · m y ρ2 = 28,38Ω · m ρ2 /ρ1 = 1,11Ω · m ρa /ρ1 = 1,07, es seleccionado de la Figura A.0.7. a h =4 95 ρa del terreno 4. Figura A.0.7: Gráca de Sunde del terreno 4. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 27,31Ω · m Se selecciona el valor de separación a = 1,74m 96 de la curva en la Figura A.0.8. Figura A.0.8: Curva de resistividad aparente del terreno 4. h) La profundidad del nivel superior (h) es h= a a h = 0,44m Modelamiento para el terreno 5 a) En la Figura A.0.10 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 25,15Ω · m y ρ2 = 36,83Ω · m ρ2 /ρ1 = 1,46Ω · m ρa /ρ1 = 1,27, es seleccionado de la Figura A.0.9. a h = 2,5 97 ρa del terreno 5. Figura A.0.9: Gráca de Sunde del terreno 5. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 31,94Ω · m Se selecciona el valor de separación a = 2,56m 98 de la curva en la Figura A.0.10. Figura A.0.10: Curva de resistividad aparente del terreno 5. h) La profundidad del nivel superior (h) es h= a a h = 1,02m Modelamiento para el terreno 6 a) En la Figura A.0.12 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 31,67Ω · m y ρ2 = 31,90Ω · m ρ2 /ρ1 = 1,01Ω · m ρa /ρ1 = 1, es seleccionado de la Figura A.0.11. a h =5 99 ρa del terreno 6. Figura A.0.11: Gráca de Sunde del terreno 6. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 31,67Ω · m Se selecciona el valor de separación a = 1m de la curva en la Figura A.0.12. 100 Figura A.0.12: Curva de resistividad aparente del terreno 6. h) La profundidad del nivel superior (h) es h= a a h = 0,2m Modelamiento para el terreno 7 a) En la Figura A.0.14 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 25,98Ω · m y ρ2 = 47,25Ω · m ρ2 /ρ1 = 1,82Ω · m ρa /ρ1 = 1,40, es seleccionado de la Figura A.0.13. a h = 2,1 101 ρa del terreno 7. Figura A.0.13: Gráca de Sunde del terreno 7. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 36,37Ω · m Se selecciona el valor de separación a = 2,40m de la curva en la Figura A.0.14. 102 Figura A.0.14: Curva de resistividad aparente del terreno 7. h) La profundidad del nivel superior (h) es h= a a h = 1,14m Modelamiento para el terreno 8 a) En la Figura A.0.16 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 41,70Ω · m y ρ2 = 46,13Ω · m ρ2 /ρ1 = 1,11Ω · m ρa /ρ1 = 1,07, es seleccionado de la Figura A.0.15. a h =4 103 ρa del terreno 8. Figura A.0.15: Gráca de Sunde del terreno 8. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 44,62Ω · m Se selecciona el valor de separación a = 2,00m de la curva en la Figura A.0.16. 104 Figura A.0.16: Curva de resistividad aparente del terreno 8. h) La profundidad del nivel superior (h) es h= a a h = 0,50m Modelamiento para el terreno 9 a) En la Figura A.0.18 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 45,20Ω · m y ρ2 = 61,30Ω · m ρ2 /ρ1 = 1,36Ω · m ρa /ρ1 = 1,25, es seleccionado de la Figura A.0.17. a h = 2,8 105 ρa del terreno 9. Figura A.0.17: Gráca de Sunde del terreno 9. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 56,50Ω · m Se selecciona el valor de separación a = 2,41m de la curva en la Figura A.0.18. 106 Figura A.0.18: Curva de resistividad aparente del terreno 9. h) La profundidad del nivel superior (h) es h= a a h = 0,86m Modelamiento para el terreno 10 a) En la Figura A.0.20 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 48,53Ω · m y ρ2 = 81,78Ω · m ρ2 /ρ1 = 1,69Ω · m ρa /ρ1 = 1,34, es seleccionado de la Figura A.0.19. a h = 2,3 107 ρa del terreno 10. Figura A.0.19: Gráca de Sunde del terreno 10. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 65,02Ω · m Se selecciona el valor de separación a = 2,34m de la curva en la Figura A.0.20. 108 Figura A.0.20: Curva de resistividad aparente del terreno 10. h) La profundidad del nivel superior (h) es h= a a h = 1,02m Modelamiento para el terreno 11 a) En la Figura A.0.22 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 83,58Ω · m y ρ2 = 96,05Ω · m ρ2 /ρ1 = 1,15Ω · m ρa /ρ1 = 1,08, es seleccionado de la Figura A.0.21. a h =4 109 ρa del terreno 11 Figura A.0.21: Gráca de Sunde del terreno 11. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 90,26Ω · m Se selecciona el valor de separación a = 1,76m de la curva en la Figura A.0.22. 110 Figura A.0.22: Curva de resistividad aparente del terreno 11. h) La profundidad del nivel superior (h) es h= a a h = 0,44m Modelamiento para el terreno 12 a) En la Figura A.0.24 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 86,30Ω · m y ρ2 = 108,80Ω · m ρ2 /ρ1 = 1,26Ω · m ρa /ρ1 = 1,19, es seleccionado de la Figura A.0.23. a h = 3,1 111 ρa del terreno 12 Figura A.0.23: Gráca de Sunde del terreno 12. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 102,70Ω · m Se selecciona el valor de separación a = 2,02m de la curva en la Figura A.0.24. 112 Figura A.0.24: Curva de resistividad aparente del terreno 12. h) La profundidad del nivel superior (h) es h= a a h = 0,65m Modelamiento para el terreno 13 a) En la Figura A.0.26 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 105,65Ω · m y ρ2 = 107,17Ω · m ρ2 /ρ1 = 1,01Ω · m ρa /ρ1 = 1, es seleccionado de la Figura A.0.25. a h =5 113 ρa del terreno 13 Figura A.0.25: Gráca de Sunde del terreno 13. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 105,65Ω · m Se selecciona el valor de separación a = 1,00m de la curva en la Figura A.0.26. 114 Figura A.0.26: Curva de resistividad aparente del terreno 13. h) La profundidad del nivel superior (h) es h= a a h = 0,20m Modelamiento para el terreno 14 a) En la Figura A.0.28 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 107,25Ω · m y ρ2 = 109,95Ω · m ρ2 /ρ1 = 1,03Ω · m ρa /ρ1 = 1,00, es seleccionado de la Figura A.0.27. a h =5 115 ρa del terreno 14 Figura A.0.27: Gráca de Sunde del terreno 14. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 107,25Ω · m Se selecciona el valor de separación a = 1,00m de la curva en la Figura A.0.28. 116 Figura A.0.28: Curva de resistividad aparente del terreno 14. h) La profundidad del nivel superior (h) es h= a a h = 0,20m Modelamiento para el terreno 15 a) En la Figura A.0.30 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 147,80Ω · m y ρ2 = 176,15Ω · m ρ2 /ρ1 = 1,19Ω · m ρa /ρ1 = 1,14, es seleccionado de la Figura A.0.29. a h = 3,5 117 ρa del terreno 15 Figura A.0.29: Gráca de Sunde del terreno 15. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 168,49Ω · m Se selecciona el valor de separación a = 1,56m de la curva en la Figura A.0.30. 118 Figura A.0.30: Curva de resistividad aparente del terreno 15. h) La profundidad del nivel superior (h) es h= a a h = 0,45m Modelamiento para el terreno 16 a) En la Figura A.0.32 se observa la curva de resistividad aparente b) Se estiman los valores de c) Se calcula d) El valor de e) Se observa que el valor de ρ1 = 155,75Ω · m y ρ2 = 190,50Ω · m ρ2 /ρ1 = 1,22Ω · m ρa /ρ1 = 1,16, es seleccionado de la Figura A.0.31. a h = 3,5 119 ρa del terreno 16 Figura A.0.31: Gráca de Sunde del terreno 16. f) El valor de la resistividad aparente (ρa ) es: ρa = g) ρa ρ1 ∗ ρ1 = 180,67Ω · m Se selecciona el valor de separación a = 2,00m de la curva en la Figura A.0.32. 120 Figura A.0.32: Curva de resistividad aparente del terreno 16. h) La profundidad del nivel superior (h) es h= a a h = 0,57m 121 Anexo B MÉTODO DE INSTALACIÓN DEL ELECTRODO QUÍMICO 122 Tabla B.1: Método de instalación del Electrodo Químico [2]. 123 Anexo C TABLAS 124 Tabla C.1: Fórmulas para calcular la resistencia de puesta a tierra de distintas conguraciones [11]. 125 Tabla C.2: Propiedades de los conductores [9]. 126 Tabla C.3: Diagrama de bloques del procedimiento del diseño según el estándar IEEE 80-2013 [8]. 127 Anexo D MEDICIÓN DE LA RESISTENCIA POR EL MÉTODO DE CAÍDA DE POTENCIAL 128 Para la medición de la resistencia de puesta a tierra mediante el método de la caída de potencial (62 %), se seleccionan unos valores estándar para la colocación de las picas auxiliares para medir todos los diseños. Tomando en cuenta de que la pica de corriente se encuentre al menos 5 veces la longitud del electrodo bajo prueba, y la pica de tensión se encuentra al 62 % de la distancia ”D” como se observa en la Figura 1.5.4. En las siguientes tablas se da a conocer los resultados de resistencia para cada medición, seleccionando un diseño de cada terreno. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T1.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 7.20 20 12.4 7.23 15 9.3 7.22 Resistencia promedio 7.22 Tabla D.1: Medición de la resistencia a tierra del diseño T1.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T2.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 7.00 20 12.4 6.95 15 9.3 6.91 Resistencia promedio 6.95 Tabla D.2: Medición de la resistencia a tierra del diseño T2.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T3.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 10.09 20 12.4 10.02 15 9.3 10.00 Resistencia promedio 10.04 Tabla D.3: Medición de la resistencia a tierra del diseño T3.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T4.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 14.05 20 12.4 14.05 9.3 13.84 15 Resistencia promedio 13.98 Tabla D.4: Medición de la resistencia a tierra del diseño T4.1 por el método del 62 %. 129 En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T5.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 13.21 20 12.4 13.20 15 9.3 13.20 Resistencia promedio 13.20 Tabla D.5: Medición de la resistencia a tierra del diseño T5.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T6.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 10.45 20 12.4 10.46 15 9.3 Resistencia promedio 9.70 10.20 Tabla D.6: Medición de la resistencia a tierra del diseño T6.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T7.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 10.59 20 12.4 10.57 15 9.3 10.48 Resistencia promedio 10.55 Tabla D.7: Medición de la resistencia a tierra del diseño T7.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T8.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 21.60 20 12.4 21.80 15 9.3 22.00 Resistencia promedio 21.80 Tabla D.8: Medición de la resistencia a tierra del diseño T8.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T9.1. 130 Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 26.30 20 12.4 26.20 15 9.3 26.60 Resistencia promedio 26.37 Tabla D.9: Medición de la resistencia a tierra del diseño T9.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T10.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 28.00 20 12.4 28.00 15 9.3 28.10 Resistencia promedio 28.03 Tabla D.10: Medición de la resistencia a tierra del diseño T10.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T11.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 43.60 20 12.4 43.40 15 9.3 43.20 Resistencia promedio 43.40 Tabla D.11: Medición de la resistencia a tierra del diseño T11.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T12.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 48.60 20 12.4 48.00 15 9.3 47.50 Resistencia promedio 48.03 Tabla D.12: Medición de la resistencia a tierra del diseño T12.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T13.1. 131 Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 47.30 20 12.4 47.50 15 9.3 48.10 Resistencia promedio 47.63 Tabla D.13: Medición de la resistencia a tierra del diseño T13.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T14.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 57.80 20 12.4 57.30 15 9.3 57.10 Resistencia promedio 57.40 Tabla D.14: Medición de la resistencia a tierra del diseño T14.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T15.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 70.70 20 12.4 70.70 15 9.3 70.50 Resistencia promedio 70.63 Tabla D.15: Medición de la resistencia a tierra del diseño T15.1 por el método del 62 %. En la Tabla D, se muestra los resultados obtenidos mediante el método de caída de potencial del diseño T16.1. Posición de la pica de corriente (CP ) Posición de la pica de (P P ) [m] tensión [m] Resistencia [Ω] 25 15.5 143.80 20 12.4 143.50 15 9.3 143.40 Resistencia promedio 143.57 Tabla D.16: Medición de la resistencia a tierra del diseño T16.1 por el método del 62 %. 132 Anexo E DISEÑOS DE SISTEMAS DE PUESTA A TIERRA 133 Diseños de Sistemas de Puesta a Tierra para una resistencia de 20Ω Varilla copperweld: 1.8m x 5/8 Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 1-38 x x x 39-71 d=3[m] x x 72-85 d=5[m] x x x 86-104 d=3[m] x xx x x 105-156 d=5[m] x x x x 157-188 d=4[m] 189-218 d=5[m] 219-248 d=6[m] x x x x 249-288 d=5[m] x x Tabla E.1: Diseños recomendados para obtener una resistencia de 20 ohm usando conductor (horizontal) y varillas (vertical). 134 Diseños de Sistemas de Puesta a Tierra para una resistencia de 20Ω Varilla copperweld: 1.8m x 5/8 + GEM BenzoElectric Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 39-55 x x x 56-102 d=3[m] x x 103-122 d=5[m] x x x 123-148 d=3[m] x xx x x 149-223 d=5[m] x x x x 224-269 d=4[m] x x Tabla E.2: Diseños recomendados para obtener una resistencia de 20 ohm usando GEM BenzoElectric. 135 Diseños de Sistemas de Puesta a Tierra para una resistencia de 20Ω Varilla copperweld: 1.8m x 5/8 + GEM Cadweld Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 39-64 x x x 65-119 d=3[m] x x 120-143 d=5[m] x x x 144-173 d=3[m] x xx x x 174-260 d=5[m] x x Tabla E.3: Diseños recomendados para obtener una resistencia de 20 ohm usando GEM Cadweld. 136 Diseños de Sistemas de Puesta a Tierra para una resistencia de 10Ω Varilla copperweld: 1.8m x 5/8 Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 1-19 x x x 20-35 d=3[m] x x 36-42 d=5[m] x x x 43-52 d=3[m] x xx x x 53-78 d=5[m] x x x 79-94 d=4[m] x x 95-124 d=6[m] x x x 125-144 d=5[m] 145-165 d=6[m] 166-187 d=7[m] x x x x 188-235 d=6[m] x x 236-267 d=7[m] x x Tabla E.4: Diseños recomendados para obtener una resistencia de 10 ohm usando conductor (horizontal) y varillas (vertical). 137 Diseños de Sistemas de Puesta a Tierra para una resistencia de 10Ω Varilla copperweld: 1.8m x 5/8 + GEM BenzoElectric Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 20-27 x x x 28-51 d=3[m] x x 53-61 d=5[m] x x x 62-74 d=3[m] x xx x x 75-111 d=5[m] x x x x 112-134 d=4[m] x x 135-177 d=6[m] x x x x 178-206 d=5[m] 207-237 d=6[m] 238-267 d=7[m] x x Tabla E.5: Diseños recomendados para obtener una resistencia de 10 ohm usando GEM BenzoElectric. 138 Diseños de Sistemas de Puesta a Tierra para una resistencia de 10Ω Varilla copperweld: 1.8m x 5/8 + GEM Cadweld Conductor de cobre desnudo #2 AWG Profundidad de los conductores: Rango de resistividad Ω·m Separación (d) [m] h = 0,25m Conguración x x 19-32 x x x 33-59 d=3[m] x x 60-71 d=5[m] x x x 72-86 d=3[m] x xx x x 87-130 d=5[m] x x x 131-157 x x d=4[m] x 158-206 d=5[m] x x x 207-240 d=5[m] x x 241-276 d=6[m] x x Tabla E.6: Diseños recomendados para obtener una resistencia de 10 ohm usando GEM Cadweld. 139