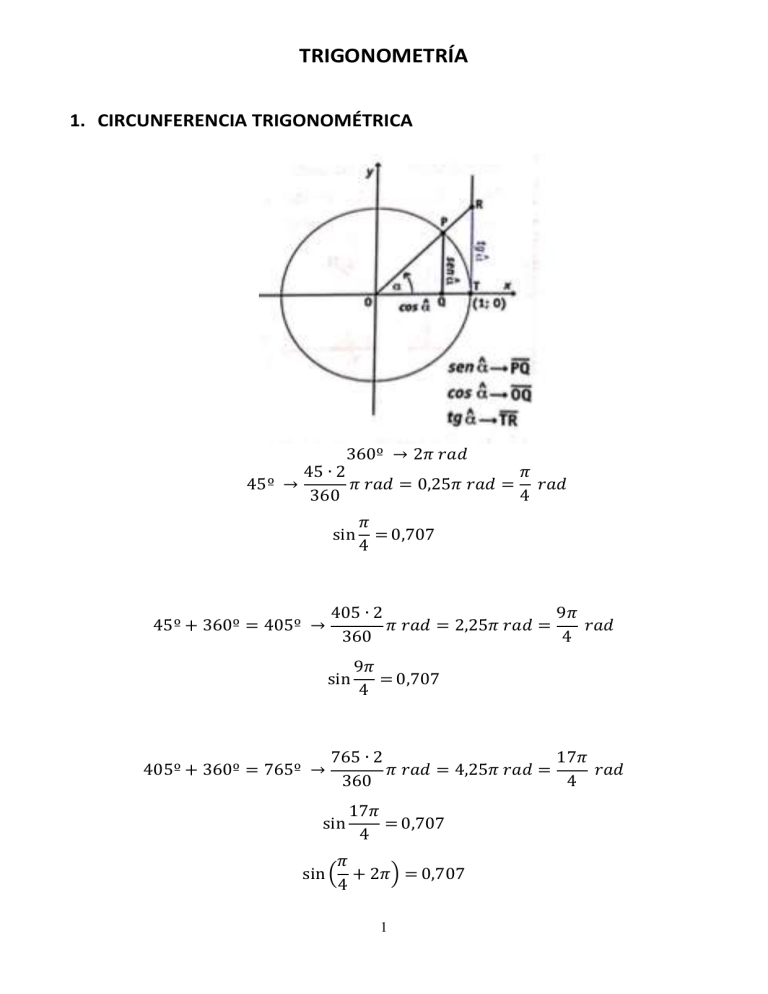
TRIGONOMETRÍA 1. CIRCUNFERENCIA TRIGONOMÉTRICA 360º → 2𝜋 𝑟𝑎𝑑 45º → 45 ∙ 2 𝜋 𝜋 𝑟𝑎𝑑 = 0,25𝜋 𝑟𝑎𝑑 = 𝑟𝑎𝑑 360 4 sin 45º + 360º = 405º → 405 ∙ 2 9𝜋 𝜋 𝑟𝑎𝑑 = 2,25𝜋 𝑟𝑎𝑑 = 𝑟𝑎𝑑 360 4 sin 405º + 360º = 765º → 𝜋 = 0,707 4 9𝜋 = 0,707 4 765 ∙ 2 17𝜋 𝜋 𝑟𝑎𝑑 = 4,25𝜋 𝑟𝑎𝑑 = 𝑟𝑎𝑑 360 4 sin 17𝜋 = 0,707 4 𝜋 sin ( + 2𝜋) = 0,707 4 1 𝜋 sin ( + 4𝜋) = 0,707 4 𝜋 sin ( + 6𝜋) = 0,707 4 𝜋 sin ( + 2𝑘𝜋) = 0,707 𝑐𝑜𝑛 𝑘 ∈ 𝑍 4 2. GRÁFICA DE SENO Para todos los ángulos que dentro de la circunferencia tienen la misma posición gráfica, el valor del seno (y del coseno) es el mismo. 𝜋 sin ( ) = 0,866 3 𝜋 7𝜋 + 2𝜋 = 3 3 sin ( 7𝜋 ) = 0,866 3 3. SIGNOS DE LAS FUNCIONES TRIGONOMÉTRICAS 2 4. VALORES CORRIENTES 3 5. EJEMPLOS a) sin 𝑥 = 1 2 1 𝑥 = 𝑎𝑟𝑐 sin ( ) 2 𝑥1 = 𝑥2 = ( 𝜋 + 2𝑘𝜋, 6 5𝜋 ) + 2𝑘𝜋, 6 𝜋 5𝜋 𝜋− = 6 6 4 𝑘∈𝑍 𝑘∈𝑍 b) cos(2𝑥) = 3 2 3 2𝑥 = 𝑎𝑟𝑐 cos ( ) 2 No podes hacerlo porque sabemos que tanto el seno como el coseno tiene una amplitud de 1, o sea varía entre 1 y -1. Por lo tanto al ser 3/2 mayor que 1, no lo reconoce. 𝑆𝑜𝑙: ∄𝑥 cos(2𝑥) = 3 2 cos 2 𝑥 − sin2 𝑥 = 3 2 3 1 − sin2 𝑥 − sin2 𝑥 = 2 3 1 − 2 sin2 𝑥 = 2 1 2 sin2 𝑥 = − 2 1 sin2 𝑥 = − 4 5 c) cos 2 𝑥 − sin2 𝑥 = 1 (1 − sin2 𝑥) − sin2 𝑥 = 1 1 − 2 sin2 𝑥 = 1 2 sin2 𝑥 = 0 sin2 𝑥 = 0 sin 𝑥 = 0 𝑥1 = 0 + 2𝑘𝜋, 𝑘∈𝑍 𝑥2 = 𝜋 + 2𝑘𝜋, 𝑥2 = (2𝑘 + 1)𝜋, 𝑘∈𝑍 𝑘∈𝑍 d) cos 2 𝑥 + sin2 𝑥 = 1 1 − sin2 𝑥 + sin2 𝑥 = 1 1=1 𝑠𝑜𝑙: ∀𝑥 ∈ 𝑅 Para todo valor de x que pertenece a los reales e) sin(2𝑥) = 2 sin(2𝑥) cos(𝑥) 2 sin 𝑥 cos 𝑥 = 2 ∙ 2 sin 𝑥 cos 𝑥 ∙ cos 𝑥 2 sin 𝑥 cos 𝑥 = 4 sin 𝑥 cos 𝑥 ∙ cos 𝑥 2 = 4 cos 𝑥 cos 𝑥 = 1 2 𝑥1 = 𝜋 + 2𝑘𝜋, 3 𝑘∈𝑍 𝑥2 = 5𝜋 + 2𝑘𝜋, 3 𝑘∈𝑍 6 f) 𝜋 √2 (cos 𝑥 − sin 𝑥) cos (𝑥 + ) = 4 2 𝜋 𝜋 √2 √2 cos 𝑥 ∙ cos − sin 𝑥 ∙ sin = cos 𝑥 − sin 𝑥 4 4 2 2 cos 𝑥 ∙ √2 √2 √2 √2 − sin 𝑥 ∙ = cos 𝑥 − sin 𝑥 2 2 2 2 √2 √2 √2 √2 cos 𝑥 − sin 𝑥 = cos 𝑥 − sin 𝑥 2 2 2 2 0=0 𝑠𝑜𝑙: ∀𝑥 ∈ 𝑅 7

![Transforma la integral / (x2 " y2) dx ] dy a coordenadas polares y](http://s2.studylib.es/store/data/005336881_1-38107913b0406391f278007c215c7e11-300x300.png)







