Lógica y Lenguajes formales
Anuncio
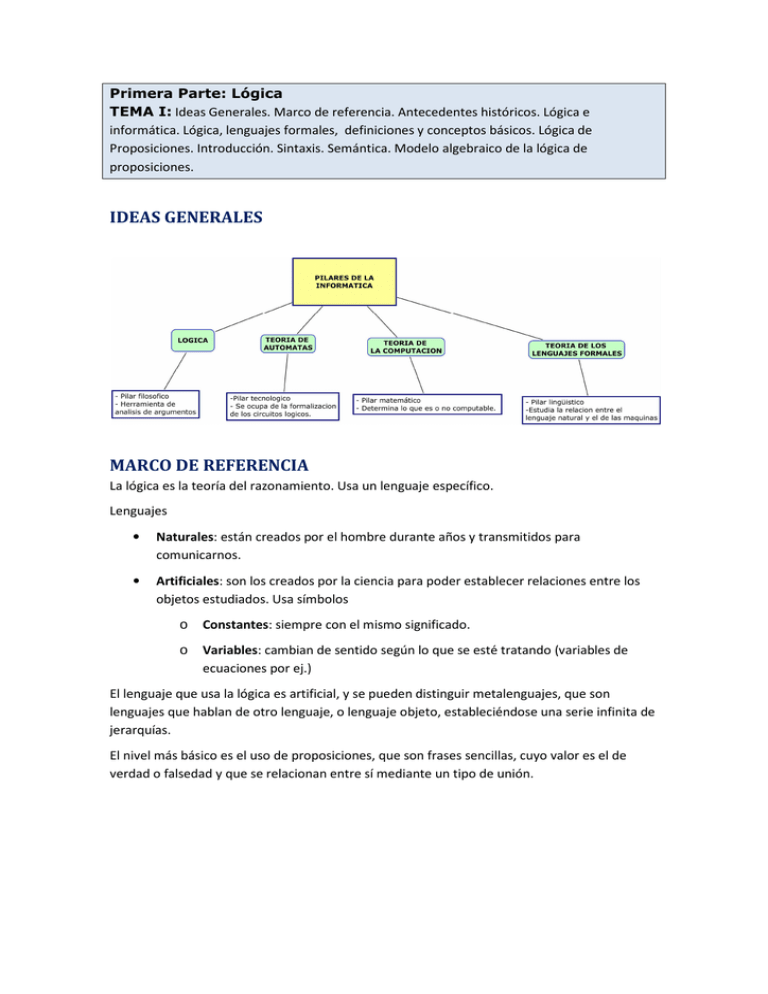
Primera Parte: Lógica TEMA I: Ideas Generales. Marco de referencia. Antecedentes históricos. Lógica e informática. Lógica, lenguajes formales, definiciones y conceptos básicos. Lógica de Proposiciones. Introducción. Sintaxis. Semántica. Modelo algebraico de la lógica de proposiciones. IDEAS GENERALES MARCO DE REFERENCIA La lógica es la teoría del razonamiento. Usa un lenguaje específico. Lenguajes • Naturales: están creados por el hombre durante años y transmitidos para comunicarnos. • Artificiales: son los creados por la ciencia para poder establecer relaciones entre los objetos estudiados. Usa símbolos o Constantes: siempre con el mismo significado. o Variables: cambian de sentido según lo que se esté tratando (variables de ecuaciones por ej.) El lenguaje que usa la lógica es artificial, y se pueden distinguir metalenguajes, que son lenguajes que hablan de otro lenguaje, o lenguaje objeto, estableciéndose una serie infinita de jerarquías. El nivel más básico es el uso de proposiciones, que son frases sencillas, cuyo valor es el de verdad o falsedad y que se relacionan entre sí mediante un tipo de unión. ANTENCEDENTES HISTORICOS 1º ETAPA 2º ETAPA 3º ETAPA •S.IV S.IV AC, Aristoteles usa la logica de predicados, o logica clasica , para identificar y utillizar las formas del razonamiento humano. •S. S. XII, S. Tomás de Aquino utiliza esto para discusiones teologicas. •S. S. XVI, Leibniz aplica la logica a las matematicas para probar teoremas, pero sin exito hasta 120 años despues. S. XIX, Boole modelo algebraico de la logica de proposiciones, Frege concepto de cuantificador. •S. •Morgan, Morgan, leyes para la conjuncion y disyuncion. •Russell, Russell, aritmetica relacionada con la logica, y axiomas. •Aparicion Aparicion de los ordenadores mitad del siglo XX. •Se Se usan en el procesamiento automatico de inferencias, estrategias de programacion, lenguajes, probabilidades. EL LENGUAJE DE LA LÓGICA DE PROPOSICIONES Semántica Es el estudio del significado. Ahora se le asigna a cada proposición un valor de verdad. Hay varias asignaciones, y cada resultado es una interpretación. La tabla de verdad es el conjunto de todas las interpretaciones posibles de una sentencia. La tabla siguiente es la de las relaciones más usadas. p V V F F q V F V F no p F F V V pyq V F F F poq V V V F p⨁ ⨁q F V V F p→ →q V F V V p↔ ↔q V F F V Dos sentencias son equivalentes si tienen la misma tabla de verdad. Se establece una relación de equivalencia que cumple las propiedades reflexiva, simétrica y transitiva, y agrupa las sentencias en clases de equivalencia según la tabla de verdad que represente. Para dos variables, existen 16 clases, siendo la C0 la tautología, y la C15 la contradicción.











