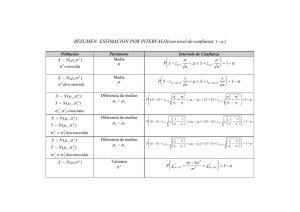
BIOESTADISTICA I UNIDAD: INFERENCIA ESTADISTICA EJERCICIOS Y PROBLEMAS 2016 I- INFERENCIA ESTADISTICA La Teoría de la Inferencia Estadística puede definirse como aquellos métodos que permiten hacer inferencias o generalizaciones sobre una población a partir de una muestra. Existen dos métodos para estimar parámetros de la población : El Método Clásico y Método Bayesiano. El Método Clásico .- Se basa estrictamente en la información obtenida en una muestra aleatoria tomada de una población. • El Método Bayesiano.- Utiliza el conocimiento subjetivo previo acerca de la distribución de probabilidades de los parámetros desconocidos junto con la información proporcionada por los datos de la muestra. La Inferencia Estadística puede dividirse en dos áreas principales : • Estimación y Prueba de Hipótesis. 2.1 ESTIMACION La Estimación se ocupa del estudio de parámetros de la población y consiste en encontrar o determinar una estadística que constituya una buena estimación del valor de un parámetro desconocido . A esta estadística se le llama estimador del parámetro desconocido . Estudiaremos la estimación puntual y la estimación por intervalos . 2.1.1 ESTIMACIÓN PUNTUAL La Estimación Puntual de algún parámetro de la población es un valor simple de una estadística tomada de la muestra. Por ejemplo, si el valor de x es la estadística calculada a partir de una muestra de tamaño n, entonces x es una estimación puntual de media población, es decir ˆ = x y =. La Estadística que se emplea para obtener una estimación puntual recibe el nombre de “Estimador “. PROPIEDADES DESEABLES DE LOS ESTIMADORES PUNTUALES a) Estimador insesgado Si tenemos un gran número de muestras de tamaño n y obtenemos el valor del estimador en cada una de ellas, sería deseable que la media de todas estas estimaciones coincidiera con el valor de μ . Se dice que un estimador es insesgado si su esperanza matemática coincide con el valor del parámetro a estimar. E ˆ b) Estimador eficiente Se dice que los estimadores son eficientes cuando generan una distribución muestral con el mínimo error estándar ,es decir, entre dos estimadores insesgados de un parámetro dado es má.s eficiente el de menor varianza Es decir si ˆ1 y ˆ2 son dos estimadores de , si V( ˆ1 ) V (ˆ2 ) entonces ˆ1 será más eficiente que 2 c) Estimador consistente Un estimador se dice consistente cuando su valor tiende hacia el verdadero valor del parámetro a medida que aumenta el tamaño de la muestra . Es decir, la probabilidad de que la estimación sea el verdadero valor del parámetro tiende a 1. d) Estimador suficiente Se dice de un estimador que es suficiente cuando es capaz de extraer de los datos toda la información importante sobre el parámetro. Ejemplo: • Los siguientes datos corresponden a los valores de una muestra de la actividad (micro moles por minuto por gramo de tejido) de cierta enzima medida en el tejido gástrico normal de 35 pacientes con carcinoma gástrico. .350 1.827 .372 .610 .521 .614 .411 1.189 .537 .898 .3.19 .603 .374 .406 .533 .788 .449 .348 .413 .662 .273 .262 1.925 .767 1.177 2.464 .448 .550 .385 .307 .571 .971 .622 .774 1.499 Determinar: a) b) c) d) La estimación de la media poblacional La estimación de la varianza poblacional Cual es la desviación estándar de la muestra Cual es la estimación del error estándar para la media muestral e) La proporción de pacientes que tienen por debajo del .600 de la actividad de la enzima medida en tejido gástrico normal. f) Estime el total de enzima que tienen esta enfermedad si se tiene una población de 4800 Pacientes en la población. 1.2 ESTIMACION POR INTERVALOS E n vez de estimar el parámetro a partir de un valor ( estimación puntual ) ahora se trata de estimar un intervalo [ a, b ] llamado intervalo de confianza que debe contener al parámetro con una probabilidad dada 1 - llamado nivel de confianza , en base a una muestra aleatoria y la correspondiente estadística ; esto es : P ( a b) = 1 - 2.2.1 ) INTERVALOS CONFIDENCIALES PARA LA MEDIA POBLACIONAL a1 ) Cuando es conocida o n > 30 Sea x ( , 2n ) Z = (x - ) / ( n ) P ( - Z 2 < ( (x - ) / ( n ) < Z 2 ) = 1 - P ( x – Z n < < x + Z n ) = 1 - Por lo tanto [x – Z n ] Donde : x : media muestral Z : se encuentra en la tabla Z n. : tamaño de la muestra : desviación estándar conocida : nivel de significación NOTA.-Cuando n 30 y no se conoce 2 se reemplaza por s2 de la muestra Ejemplo Se ha calculado que la media y desviación estándar de una muestra aleatoria de 36 mediciones del contenido de arsénico del agua del reservorio de la Ciudad Universitaria son respectivamente 2.6 y 0.3 …. ¿Encuentre el intervalo de confianza al 95% y al 99% para la media de arsénico de todo el reservorio ?. Solución: x = 2.6 s = 0.3 /2 = 0.025 Z = 1.96 P ( 2.6 – 1.96 (0.3/36) 2.6 + 1.96 (0.3/36) ) = 95% De donde P( 2.5 < < 2.7 ) = 95% La probabilidad de que la medición promedio del contenido de arsénico se encuentre entre 2.5 y 2.7 es de 95% . a2) Cuando es desconocido n 30 Cuando no se conoce la varianza poblacional 2 y es imposible obtener una muestra n 30 pues el costo es un factor que limita el mayor tamaño de muestra. En la medida que la población se distribuye normalmente entonces podemos usar la distribución t. t = (x - )/ ( s/ n) El procedimiento es el mismo que en el caso anterior excepto que se usa la distribución T en lugar de la normal, luego se puede afirmar: P ( - t/2 P ( x <t< t/2 ) - t/2 s /n < < x + t/2 s/n ) = 1 - Por lo tanto x donde t/2 = 1- t/2 s/n es el valor de t con n – 1 grados de libertad Ejemplo 1 • Lloyd y Mailloux informaron los siguientes datos acerca del peso de la glándula pituitaria en una muestra de 4 ratas de Wistar Furth • Media = 9.0 mg error estándar para la media =3 • Determinar: • La desviación estándar para la muestra • Construya un intervalo de confianza de 95% para el peso medio de las glándulas pituitarias para una población similar de ratas . Ejemplo Los contenidos de ácido sulfúrico en siete recipientes similares son : 9.8 , 10.2 , 10.4 , 9.8 , 10.0 , 10.2 y 9.6 litros. Encuentre un intervalo de confianza al 95% para la media del contenido de todos los recipientes. Suponiendo una distribución aproximadamente normal. Solución: x = 10 ; s = 0.283 ; t/2 luego : x t/2 s/n 10.0 ( 2.447 ) ( 0.283)/ 7 10.0 0.26 P ( 9.74 < < 10.26 ) = 95 % = t (0.025) (6) = 2.447 B) INTERVALOS DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS Si se tiene una población con medias 1 , 2 y varianzas 12 , 22 respectivamente y si se toma muestras n1 y n2 respectivamente, entonces se puede obtener intervalos confidenciales para la diferencia de medias. b1) Si 12 , 22 son conocidas y n 1 30 y n2 30 entonces un intervalo confidencial para 1 - 2 es: P [( x1 --x2 ) - Z (12 / n1 + 22 /n2 ) 1 - 2 (x1 -x2 ) + Z (12 / n1 + 22 /n2 ) ] = 1 - por lo tanto ( 1 - 2 ) [( x1 --x2 ) Z (12 / n1 + 22 /n2 )] Donde x1 ,x2 son las medias muestras aleatorias independientes de tamaño n1 , n2 , tomadas de poblaciones con varianzas conocidas 12 , 22 respectivamente, y - Z es el valor de la distribución normal estándar. Ejemplo : 50 Mujeres y 76 hombres se presentaron a un examen de admisión para ocupar un cargo : las mujeres obtienen una calificación promedio de 76 puntos con una desviación estándar de 6 , mientras que los hombres obtienen una calificación promedio de 82 puntos con una desviación estándar de 8. Encuentre un intervalo de confianza del 96% para la diferencia de medias. SOLUCI0N n1 = 50 n2 = 75 , x1 = 76 y x2 = 82 Como n1 , n2 > 30 s1 = 1 y s 2 = 2 , s1 = 6 y s2 = 8 Z(0.98)= Se aplica P [( x1 --x2 ) - Z (12 / n1 + 22 /n2 ) 1 - 2 (x1 -x2 ) + Z (12 / n1 + 22 /n2 ) ] = 1 - P [( -6 ) –2.054 36/ 50 + 64/75 ) 1 - 2 (-6 ) +-2.054 (36/ 50 + 64 /75 ) ] = 1 - Remplazando datos se obtiene : P ( -8.57 ) 1 - 2 - 3.42 ) = 95 % b2 ) Si 12 , 22 son desconocidas y n 1 y n2 30 Donde las medias y varianzas de muestras independientes pequeñas de tamaños n1 y n2 son tomadas de distribuciones aproximadamente normales y t es el valor de la distribución t con n1 + n2 - 2 grados de libertad: P [( x1 --x2 ) - t (s12 / n1 + s22 /n2 ) 1 - 2 (x1 -x2 ) + t (s12 / n1 + s22 /n2 ) ] = 1 - por lo tanto ( 1 - 2 ) [( x1 --x2 ) t (s12 / n1 + s22 /n2 )] Ejemplo: Los registros de los últimos 15 años muestran que la precipitación fluvial promedio. durante el mes de mayo es de 4.93 cm. con una desviación estándar 1.14 cm. en Perú, en Chile la precipitación fluvial promedio fue de 2.64 con una desviación estándar de 0.66 durante los 10 años pasados. Encuentre un intervalo confidencial del 95% para la diferencia verdadera de las precipitaciones fluviales promedio en estos países, suponiendo que las muestras se han tomado de poblaciones normales con variancias diferentes. Solución: Perú x = 4.93 Chile x = 2.64 .t( 0.025 ) ( 15+10 –2 ) s = 1.14 n = 15 s = 0.66 n = 10 = 2.069. Remplazando en la fórmula se tiene : P [( 2.29 – 2.069 ) (1.142 / 15 + 0.662 /10 ) 1 - 2 2.29 + 2.069 (1.142 / 15 + 0.662 /10 ) ] = 1 - P( 1.544 1 - 2 3.036 ) = 0 95 % Significa que si se tiene una confianza del 95% de que el intervalo de 1.544 a 3.036 contenga el verdadero valor de la diferencia de medias de la precipitación fluvial real. OBS. Si el el intervalo confidencial contiene al cero enteoces no puede concluirse que existe diferencia significativa entre las medias- C) I NTERVALOS CONFIDENCIALES PARA LAS PROPORCIONES Si la estadística p = x /n es la proporción de éxitos en una muestra de tamaño n extraída de. una distribución binomial en la que P es la proporción de éxitos en la población los límites de confianza para P, cuando n se tiene que : E(p) = P , V(p) = PQ /n por lo tanto también se tiene: P ( - Z 2 < Z < Z 2 ) = 1 - Z = (p – P)/ ( PQ /n ) por lo tanto P [ p - Z 2 ( PQ /n ) < P < p +Z 2 ( PQ /n ) ] = 1 - Luego P [ p Z 2 ( PQ /n ) ] Ejemplo: En una muestra aleatoria de n = 500 familias de cierta ciudad que poseen televisores, se observó que 340 poseían TV a color. Encuentre un intervalo de confianza del 95% para la proporción real de las familias en dicha ciudad con TV a color. Solución: p = 340/500 = 0.68 Z( 0.025) = 1.96 Usando la fórmula : P [ p - Z 2 ( PQ /n ) < P < p +Z 2 ( PQ /n ) ] = 1 - P[ 0.68 – 1.96 ( 0.68*0.32) /500 < P < 0.68 + 1.96 ( 0.68*0.32) /500 ] = 95% Por lo tanto P ( 0.64 < P < 0.72 ) = 95 % D) INTERVALOS DE CONFIANZA PARA LA DIFERENCIA DE PROPORCIONES Dada dos poblaciones binomiales de las cuales se extrae dos muestras aleatorias independientes de tamaños n1, n2 se puede encontrar un intervalo de confianza para la verdadera diferencia de proporciones, es decir P1 , P 2 mediante : P [( p1 - p2 ) - Z/2 ( p1 q1 /n1 + p2 q2 /n2) < P1 – P2 < ( p1 - p2 ) + Z/2 ( p1 q1 /n1 + p2 q2 /n2)] Por lo tanto (P1 – P2 ) [ ( p1 - p2 ) Z/2 ( p1 q1 /n1 + p2 q2 /n2) ] Ejemplo: En el proceso de fabricación de cierto componente se considera un cambio con el objeto de determinar si el nuevo procedimiento es mejor. Se toma muestras del procedimiento existente y del nuevo si se detecta que 75 de 1500 componentes tomados del procedimiento existente fueron defectuosos, así como 80 de 2000 del nuevo procedimiento fueron defectuosos. Encuentre un intervalo de confianza al 90% para la diferencia real de proporción de componentes defectuosos. Solución: p1 = 75/1500 = 0.05 p2 = 80/2000 = 0.04 Según fórmula 0.01 n1 = 1500 n2 = 2000 Z/2 = 1.645 : 1.645 ( 0.05*0.95/1500 + 0.04*0.96/2000 ) P ( -0.0017 < P1– P2 < 0.0217 ) = 90 % Como el intervalo contiene el valor 0 no hay razones, que el nuevo componente produzca una disminución significativa en la proporción de componentes defectuosos con respecto al método existente. ) INTERVALOS CONFIDENCIALES PARA LA VARIANZA E Supongamos que tenemos una muestra aleatoria x1 ,x2 , x3, ... xn de una distribución de media y una varianza 2 , ambas desconocidas luego: n ( xi - x ) 2 = (n –1 ) s2 i=1 2 2 Tiene una distribución 2 con n-1 grados de libertad cuando las muestras se escogen de una población normal entonces : P (2 /2 2 (2 1- /2 ) = 2 P( ( n –1 ) s 2 1- /2 2 P ( /2 (n –1 ) s2 (2 1- /2 ) = 2 (n –1 ) s2 ) = 1 - 2 /2 1- 2 2 es la varianza de la 2 2 Donde s muestra aleatoria n, /2 y 1- /2 2 son valores de la distribución con n – 1 grados de libertad hacia la derecha. Ejemplo Un experimentador quiere verificar la variabilidad de un equipo diseñado para medir el volumen de una fuente de audio frecuencia. Tres mediciones independientes registraron con este equipo fueron 4.1 , 5.2 y 10.2. Estime 2 con un coeficiente de confianza de 0.9. Solución Si se supone normalidad en las mediciones registradas por este equipo, se puede aplicar el intervalos de confianza desarrollado anteriormente . Para los datos ofrecidos, s2 = 10.57 2 P( ( n –1 ) s 2 1- /2 2 (n –1 ) s2 ) = 1 - 2 /2 P ( 3.53 2 205.24 ) = 0.90 Obsérvese que este intervalo para muy pequeño . 2 es muy amplio, básicamente porque n es Ejemplo propuesto: Los siguientes valores son los pesos en decigramos de 10 paquetes de semilla distribuidos por cierta compañia : 46.4 , 46.1 , 45.8 , 47.0 , 46.1 , 45.9 , 45.8 , 46.8 , 45.2 y 46.0. Encuentre un intervalo de confianza al 95% para la varianza de dichos paquetes de semilla distribuidos por esta compañia.