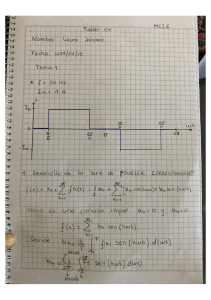
Distorsión en Amplificadores de Audio: Análisis y Medición
Anuncio

DISTORSIÓN Introducción. Distorsiones medibles. Mecanismos de audición. INTRODUCCIÓN. Existen varios tipos de distorsión. La más conocida y usada como spec es la distorsión armónica total, normalmente unida al nivel de ruido. En este caso, la distorsión producida al recortarse una onda, o al producirse una onda triangular por un slew-rate bajo puede medirse perfectamente con este parámetro. El nivel de ruido se puede considerar como una distorsión, aunque completamente diferente de la distorsión armónica. El mayor problema es que siempre hay un cierto nivel de ruido en la línea y se amplifica, llegando a ser audible. La amplificación diferencial es una buena solución para ese problema. Hay otro tipo de distorsión, poco conocida y difícil de medir, que parece ser exclusiva del campo del audio, por sus grandes ganancias y su necesidad de baja distorsión armónica, llamada transient intermodulation. En amplificación de pequeña señal, no se produce excesiva distorsión por tres motivos: Ganancias moderadas. Amplitud del voltaje reducida. Intensidad de colector(drenador) con muy pequeñas variaciones. Ninguno de estos puntos se suele cumplir en la amplificación de potencia, y la consecuencia en grandes señales es: Gran amplitud de voltaje: o distorsión por el efecto Early (en BJT y MOS). o En los mosfet: las altas capacidades CGD y CGS hacen que se reduzca el ancho de banda notablemente (aunque esto no sea propiamente una distorsión) Intensidad en el transistor: Intensidad de colector con grandes variaciones: o Variaciones muy grandes de beta o Variación de la impedancia de salida hoe o Variación de la impedancia de entrada hie o Variación de Vbe En el caso de los mosfet, intensidad de drenador con grandes variaciones: gm es variable con respecto de ID. Cuando ID es pequeña, se produce un comportamiento marcadamente alineal en todos los mosfet. Variación de la impedancia de salida Rs Variación de ID supone variación de VGS, y esto implica la carga y descarga de la capacidad equivalente de entrada Cjss Grandes ganancias: Aparición del efecto Miller. En el caso de los mosfet de potencia, cuya capacidad de entrada es alta(200pF), el problema es aún mayor. Con pequeñas ganancias, el efecto de las anteriores causas de distorsión es mínimo, pero en grandes ganancias, sus consecuencias son muy notables. inicio DISTORSIONES MEDIBLES La tendencia de las etapas de muy alta gama, ya asentadas en el mercado y con un buen número de seguidores incondicionales es reducir el factor de realimentación negativa, incluso a costa de una mayor "distorsión". Lógicamente ellos se lo pueden permitir... ¿o no? Entre un Technics con un 0,01% THD y un Gryphon con un 0,01%, ¿usted no elegiría el Gryphon? Luego algo debe haber aparte de THD. THD+N La más antigua y más básica de las distorsiones, pero la más engañosa. Consiste en una suma de la energía de cada armónico, y no indica nada sobre el orden de ellos. Como veremos, el orden de éstos armónicos es tan importante como su valor. También, a baja amplitud, el ruido se mide como otro armónico más (siendo que no está relacionado con ella) y eso no da una idea precisa de la "distorsión". Se corrige mediante la realimentación, el uso de corrientes más altas en las etapas, el uso de etapas simétricas y se genera muy especialmente en la etapa de salida. Desgraciadamente, el método que más la corrige es el que más problemas temporales crea. Desde un punto de vista teórico, THD+N es perfecta en tiempo, la distorsión es completamente paralela en el tiempo a la onda inicial, y la respuesta temporal del armónico fundamental permanece inalterada salvo por retrasos de propagación en la etapa. También desde un punto de vista teórico puede ser de lo más nocivo para el sonido o de lo menos. y lo realmente importante es cómo se genera y el orden de los armónicos. En la gráfica de la derecha podemos observar el análisis de frecuencias de una onda distorsionada (3%) procedente de un amplificador simétrico, que tienden a cancelar los armónicos de orden par Según el Teorema de Fourier cualquier función continua en un intervalo es representable mediante una serie de senos y cosenos, sin que importe que tenga escalones o que no sea derivable, lo que viene a querer decir que cualquier función por extraña que sea se puede representar mediante una suma de frecuencias puras. Arriba a la derecha, una onda cuya THD es del 38%, y es suma de simplemente tres componentes. Vemos que se producen picos curiosos y que aparentemente no hay ninguna fución que genere esa onda. A la derecha, el análisis de Fourier de la onda, donde se comprueba la existencia de sólo tres armónicos. Y en cómo se produce esta suma se basa THD, habiendo varios conceptos básicos: La distorsión armónica sólo crea armónicos de frecuencias superiores al armónico fundamental Los armónicos de orden impar tienen unos determinados efectos psicoacústicos y crea distorsiones simétricas respecto del eje X; los pares tienen otros efectos psicoacústicos y la onda resultante es asimétrica respecto del eje X THD representa cualquier distorsión, excepto las llamadas "de memoria" (térmicas y absorciones dieléctricas). Pero no todos los fenómenos que causan distorsiones armónicas causan el mismo efecto psicoacústico. Es sumamente diferente las distorsiones de orden bajo y par creada en una etapa de ganancia en voltaje, donde un 1% puede pasar inadvertido por nuestros mecanismos de audición mientras que un recorte (clipping) del 1% es sumamente molesto. Y esto es innegable, se puede comprobar fácilmente. THD se puede usar como test válido para comparar etapas, pero debe tenerse claro cual es el espectro armónico y el origen, si la etapa de salida, las de ganancia en voltaje o las sobrecargas internas de las etapas. IMD SMTPE El test SMTPE es uno de los más antiguos para esta distorsión. Existe una relación muy cercana entre THD de bajo orden e IMD ya que se suelen generar de la misma manera. A la derecha se puede ver la onda de prueba, una de 60Hz sumada a otra de 7000 Hz de un valor 4 veces menor. Pero es una representación de lo que ocurre cuando se ·"generaliza" la distorsión armónica para varias ondas, ya que en todos los casos el mecanismo de generación de THD genera también IMD. Concretamente, esta cifra se mueve en: IMD=A*THD, siendo A un número entre 3 y 4. IMD se incrementa con las variaciones bruscas en la ganancia (recorte, saturaciones, cruce por cero...) y disminuye con las funciones de transferencia suaves, por lo que esta ley no es universal, pero sí una buena aproximación. A ambos lados de la onda de más frecuencia aparecen dos ondas de +-f y nuestra percepción las enmascara, dependiendo de nuestros umbrales y de su amplitud. Pero tiene una característica: el número de armónicos creados crece al cuadrado con el número de componentes de la onda inicial. A pesar de ello es una distorsión también perfecta desde el punto de vista temporal, no explica por sí sola el barullo generado en orquestas, aunque indudablemente es una de las causas más importantes. Es una medida de cómo depende la señal del punto de operación. Todo lo que dependa del punto de operación causará IMD. Esto quiere decir que la distorsión de cruce por cero causa IMD, ya que las ondas dependen del punto de operación que generan otras. También la variación de la corriente de colector causada por el punto de operación en una etapa clase A crea IMD, poca, y un recorte crea una cantidad de IMD altísima. Al menos es útil para detectar sobrecargas. Cuanto más violenta es la variación del estado en el punto de operación más IMD se causa, es una primera aproximación a la correlación entre audición y medición. A pesar de que se genere por los mismos métodos que THD, es posible reducirla o anularla separando las bandas a amplificar, mediante la multiamplificación. CCIF El test CCIF es más apropiado para medir este fenómeno en audio. Consiste en aplicar una señal de 14kHz y 15kHz (ó 18kHz y 19kHz) y crea componentes de IMD en 1, 2, 3, 4, 5kHz... Es una medida que tiene relación con THD por que también señala una dependencia del punto de operación, es decir, una no linealidad, pero también tiene relación con la velocidad del amplificador, ya que en el punto de máxima variación de tensión se produce el doble de distorsión (también medible mediante análisis de Fourier) que THD, la cual no nos revelaría este comportamiento, si se produce. También es un test que tiene una mayor relación con la audición. Ésta distorsión está causada por errores en tiempo, a lo que somos extremadamente más sensibles que a THD de 2º orden. En el ejemplo se puede ver un análisis utilizando esta técnica. Se trata de una etapa de gran velocidad, y muy bajo factor de realimentación. En ella se puede apreciar que las componentes más distantes (1,2,3kHZ) están muy por debajo de las dos ondas de prueba, mientras que las que se pueden medir por SMTPE son más notables. THD de esta etapa es de 0,03%, lo que se corresponde con los resultados SMPTE (0,1%) y da una idea de que no se producen grandes limitaciones de velocidad, ya que la componente de 1kHz está en 0,03% Distorsiones temporales.TIM (SID) Otala, el descubridor de ésta distorsión llegó a justificar cambios audibles en base a una distorsión que hasta entonces no se había tenido en cuenta. Un ejemplo de algo que puede pasar, que bajo ciertos criterios técnicos no tenga cabida pero sí los tenga a nivel de oído. Esta distorsión se produce por la carga de corriente de uno de los condensadores más importantes en un amplificador, el de compensación en frecuencia, necesario para que un sistema realimentado funcione sin oscilar. A la derecha podemos observar un esquema de un amplificador básico: etapa diferencial con fuente de corriente y carga pasiva, etapa en clase A con carga activa y una etapa de salida push-pull en clase A (por polarización, 77mA). En la práctica el transistor usado no admite una disipación de potencia tan alta pero Spice puede ser permisivo. En la gráfica de fase y ganancia frente a frecuencia podemos ver que es estable para ganancia 10 (+20dB), que su ancho de banda es de 144kHz (-3dB) y que su margen de fase es de 93º. Podemos pensar "ningún problema". Pero no, estas cifras sólo son la punta de un iceberg. Si reproducimos una onda senoidal de 10V de 10kHz (dentro del rango audible) veremos que se produce una cantidad importante de distorsión (si es visible en una pantalla suele superar el 1%) y una desviación importante en tiempo del picos. Se ha añadido una onda senoidal de 10kHz con un desfase de -4º para poder corroborar el siguiente punto. A nivel teórico el desfase a 10kHz es de 4º y es ese el desfase medido en el armónico fundamental de la salida. No es gran cosa comparado con la distorsión que posee. Veámoslo en el análisis de frecuencias de la salida: Nº frecuencia Amplitud 1 2 3 4 5 1.000E+04 9.539E+00 2.000E+04 3.000E+04 4.000E+04 5.000E+04 2.672E-01 3.581E-01 1.153E-01 2.122E-01 Amplitud normalizada 1.000E+00 2.801E-02 3.754E-02 1.209E-02 2.225E-02 TOTAL HARMONIC DISTORTION = 5.324501E+00 PERCENT Efectivamente, un 5% de distorsión armónica es una cifra alta En las etapas diferenciales la corriente de polarización la produce una fuente constante, por lo que esta etapa nunca podrá proporcionar a ese condensador más corriente de lo que hay. En estos gráficos podemos ver los caminos de carga y descarga del condensador de Miller. Existe una relación directa entre el valor de éste condensador, la ganancia total, y la corriente de polarización. El caso es que para variaciones muy bruscas de la tensión, el condensador se carga a través de una fuente de corriente, lo que limita la tasa de variación de su voltaje. Éste es el motivo de construir amplificadores con un gran ancho de banda, no para que nuestro can oiga música supersónica, como muchas veces se ha sugerido por desconocedores de un fenómeno científico probado y relacionado con la audición, sino para que no tenga lugar ésta limitación. Esta velocidad supone cómo de rápido se va a corregir sus propios errores la etapa. Personalmente no veo necesario aumentar el ancho de banda por encima de 50kHz para que podamos oírlo, porque no podemos, pero sí veo necesario aumentarlo por encima de 100, incluso de 500kHz para poder atender a las bruscas variaciones de tensión que produce la música. En las válvulas, el transformador de salida limita el ancho de banda a 40kHz en los mejores casos, pero no produce una limitación en la tasa de variación, de ahí que sus agudos se mantengan cristalinos y que la música tenga dinamismo. Sobrecargas en los nodos internos (hard TIM) Otro de los descubrimientos de Otala, y empleado desde los albores de los tiempos por su compañía, Electrocompaniet, el concepto de TIM free. La compensación habitual y los retrasos temporales hacen que la realimentación tarde un tiempo en producirse, y cuando ésta llega, se ha amplificado una tensión que no es la adecuada. Con las grandísimas ganancias y que cuanto mayor sea el retraso, más se amplifica el error, se pueden producir (y se producen) sobrecargas en los nodos internos, saturaciones en los transistores que producen una salida de la saturación lenta. La diferencia entre la lógica digital TTL y la ECL es que en los ECL no llegan a saturar el transistor, el transistor siempre está en activa, porque salir de una saturación profunda es lento, y estos errores agravan el fenómeno. Da lugar al "grano" en el sonido, fenómeno auditivo perfectamente conocido (si tiene nombre...), pero que no se trata con la suficiente atención. Incluso hoy día, etapas consideradas de "altas prestaciones" por tener THD=0,001% tienen el polo dominante a menos de 1 Hz. Esto quiere decir que a partir de 10 Hertzios se va a producir un desfase 90º que retrasará la señal y producirá sobrecargas. Se ha aplicado la misma solución que se empleó en su día con la lógica S-TTL (TTL-Schottky), que es colocar un diodo Schottky o ultra-fast entre la base y el colector, para mejorar el tiempo de recuperación en inversa del diodo base-colector y para impedir (por su menor tensión en directa que el diodo BC) que el transistor entre en saturación profunda. Yo no puedo estar de acuerdo con esta técnica cuando lo que hay que hacer es eliminar la saturación, en vez de aliviarla. Cuando el polo dominante se pone fuera del ancho de banda útil y audible, éste fenómeno no tiene lugar en esa banda. Los problemas que causará, a pesar de existir, estarán fuera del rango audible y serán corregidos mucho más rápido, a pesar de que la inclusión de diodos BC se pueda seguir manteniendo. Curioso que un fenómeno tan nocivo y estudiado se siga manteniendo y todos los op-amp (bien de señal, bien de potencia ó gainclone) estén compensados para frecuencias siempre inferiores a 100Hz. Reducir la ganancia y aumentar el ancho de banda es la solución más viable para evitar éste fenómeno, muy difícil de medir porque prácticamente sólo ocurre en el plano temporal (sus componentes armónicas ocurren a frecuencias muy altas), que no sucede bajo condiciones periódicas y quizás por eso ignorado. Pero que causa cambios audibles. Distorsiones térmicas Existir existen, se puede comprobar en op-amp de potencia que a baja frecuencia se genera distorsión armónica que decrece con una pendiente de 6dB/oct a medida que aumenta la frecuencia. Es una causa de IMD, pero cuya acción es sumamente lenta y con gran diferencia entre las frecuencias. Puede generar componentes armónicas de IMD que afectan a frecuencias mucho mayores. Por mis experiencias puedo decir que es audible, pero difícilmente medible mediante los test convencionales. Aunque no haya podido encontrar una relación causa efecto obvia más que en etapas con grandes derivas térmicas, me baso en que cuando una etapa requiere compensación térmica (las de salida), la tonalidad no alcanza el nivel esperado hasta que no se ha producido la estabilidad térmica. Este tipo de distorsión se agrava en los integrados, donde las modulaciones térmicas en el punto de operación de las etapas se ven afectadas por la proximidad física. También es obvio que una resistencia tiene un cierto coeficiente térmico y esto varía su valor, siendo habitualmente causa de variaciones en la ganancia total y punto de operación de las etapas restantes. Además, ésta modulación es amplificada. inicio MECANISMOS DE AUDICIÓN Resulta curioso como los ciertos amplificadores de válvulas clase A con cifras altas de distorsión parecen y pueden sonar mejor y con más potencia que otro con salida en clase AB de la misma potencia. No todos los armónicos crean la misma sensación en el oyente, y tampoco se pueden ignorar las distorsiones temporales. Por esto hacemos una breve introducción a estos efectos. A la derecha vemos una curva de enmascaramiento. Según las investigaciones de la psicoacústica todo lo que queda por debajo de ciertos niveles no es audible Se puede comprobar rápidamente que toleraremos mejor los armónicos de orden bajo que los de orden alto. Utilizaremos esta notación: f0 es el armónico fundamental, y fn será el múltiplo n-ésimo de ese armónico. A n se le denomina orden del armónico. Efectos de la distorsión: timbre. El timbre resultante de una distorsión armónica tiene una estrecha relación entre su estructura de armónicos y la de un instrumento que crea una secuencia semejante. La división más sencilla es viento, cuerda y percusión. Los instrumentos de viento crean armónicos de orden 2n+1. El material del instrumento influye decisivamente en la absorción de los armónicos de orden superior. El sonido de un oboe o un clarinete (madera) es claramente diferente al de una trompeta o un flautín (metal). El módulo de Young de la madera es muy inferior al de un metal y esto influye en la velocidad a la que se propaga el sonido por el material. Por la ley de Snell, esto influye en el ángulo de refracción y en el ángulo límite entre la refracción y la reflexión. Las pérdidas de potencia acústica en un material poco rígido son mayores que en uno más rígido. Ejemplo: una copa de cristal. Además de la absorción de las ondas del material, en él también se pueden crear armónicos, que son de orden 2n. Esto ocurre principalmente en trompetas y trompas, con paredes más delgadas, y no en el flautín, con paredes más gruesas. El sonido resultante también es diferente. Las trompetas son más estridentes, aparte de que la carga espacial genera armónicos de orden par. Los instrumentos de cuerda crean principalmente armónicos de orden 2n. La diferencia del timbre la produce principalmente la tensión de la cuerda y las pérdidas que su tensión produce, y sobre todo: la caja de resonancia asociada al instrumento. A la derecha se pueden observar la onda en una cuerda sujeta por los extremos y los armónicos creados. En las cajas, el modo de creación de armónicos es semejante al de los instrumentos de viento, con unas dimensiones notablemente mayores que crean sonido por resonancia en presencia de armónicos de más baja frecuencia. Aquí sí influye el material, como en el caso del característico sonido del banjo. Los instrumentos de percusión son más complejos, ya que la creación de ondas no es igual en un xilófono que en un bombo. Las membranas (bombo, platillos, gong,..) crean armónicos de orden 2n y en los demás, como el caso de triángulos, la creación puede ser muy compleja. El material influye en el timbre, y este es el caso en el que más se manifiesta. En el caso de las campanas influye incluso la aleación. De esto se deduce en gran parte que cada instrumento tiene su timbre, y que la adición de timbre no es inocua ni mucho menos, pero en muchos casos puede pasar desapercibida o resultar beneficiosa con valores de hasta el 5% THD. En instrumentos de cuerda, la adición de armónicos de 2º y 4º orden por parte de la electrónica contribuirá a enfatizar el timbre, puede hacer que los violines suenen con más presencia, pero no será lo mismo para instrumentos de viento, donde el timbre se verá falseado. Uno de los "síntomas" de este fenómeno es que es más dificil distinguir "a oído" un instrumento de otro, en solos, un bajo de un contrabajo, ... Efectos de la distorsión: psicoacústica. Una vez superados los niveles de enmascaramiento (cosa que evidentemente ocurre, porque si no todos los amplificadores nos "sonarían" igual), y ahora que ya se han definido las clases de instrumentos y los armónicos que producen, y el número de éstos que producen dependiendo del material se puede empezar a definir el efecto de una distorsión armónica basándose en las sensaciones producidas. La caracterización del sonido está provocada principalmente por los primeros armónicos. Éstos por sí solos no aportan nada, es la combinación entre ellos los que aportan el timbre. Para empezar a clasificar, puede decirse que lo ideal es que no halla distorsión. Un amplificador no debe crear armónicos, eso lo hacen los instrumentos, pero aceptando que se crea distorsión, algún tipo puede ser más o menos molesta. En una proporción muy baja, los armónicos dan un tipo de carácter al sonido que no tiene porque ser molestos (es subjetivo), pero cuando sobrepasan un cierto nivel es cuando se convierten en un problema. En una primera clasificación, los armónicos de orden 2n crean una sensación de más vivacidad y más potencia sonora (aunque sea la misma RMS) Los armónicos de orden 2n+1 tienden a lo contrario. En los amplificadores, la distorsión creada es principalmente de segundo (f2) y tercer orden (f3), aunque también hay más. Sus efectos son: 2º: Es una octava más alto que el armónico fundamental, y es prácticamente inaudible, pero la sensación que crea es un refuerzo del sonido. Una combinación de f2 y f3 tiende a anular los efectos del f3 por separado y refuerza el sonido. 3º: Es una doceava más alto que f0, también es difícil de detectar, y tiende a debilitar el sonido. Al añadir un armónico f5 crea una sensación de instrumento de viento, de sonido sordo. A medida que crecen esos 2 últimos, la sensación se hace molesta y el sonido muy chillón. La sensación al añadir el f4 al f3 es semejante, pero esta vez con un tono de trompeta, más estridente. Los armónicos de alto orden con muy baja potencia tienden a dar un tono brillante y metálico, de gran impacto a la música, pero en el momento que crecen en amplitud, se "detectan" no como sonido separado sino como distorsión, ya que es oído humano tiene una gran sensibilidad ante tal diferencia entre las frecuencias. Uno de los efectos de esta distorsión es lo que se conoce como "grano". A partir de un cierto orden, (7º, 9º, 11º)los armónicos dejan de percibirse como relacionados con el sonido y tienden a percibirse como un ruido sucio (harsh sound, grano), como falta de consistencia con el resto del sonido, y esta sensación de incoherencia se acrecienta ante los habituales errores de fase producidos por los altavoces entre frecuencias muy distintas. Efectos de la distorsión: tipos de componente. Cada circuito tiene un tipo de distorsión característica. Las etapas clase A, suelen tener distorsión de 2º orden, por eso parecen sonar más altos los amplificadores clase A singleended. Las etapas push-pull tienden a cancelar el 2º armónico y hacen que el predominante sea el 3º, dando una sensación de sonido poco hiriente. Además, cada tipo de componente tiene un tipo de distorsión característica y predominante. En las válvulas es la de 2º orden, en transistores es 2º y 3º orden (no simétricos) y en operacionales monolíticos sólo 3º. Un armónico f7 que cree una THD de un 0,1% es audible y molesto, pero una distorsión de 2º orden con la misma THD puede no serlo. Por este motivo, un nivel de distorsión armónica de un 1% de 2º orden (como en muchos amplificadores a válvulas) puede pasar desapercibida. En conclusión, no todas las distorsiones son iguales, y aceptando que la distorsión no puede ser 0, lo mejor es que sea de 2º orden. Ganancia de un amplificador Vamos a ver, en la práctica, de dónde sale la distorsión. Tened en cuenta que los resultados y gráficos del Spice están basados en un modelo, que puede estar más o menos simplificado. Este es nuestro circuito: El transistor BC547 es un NPN muy utilizado. Lo polarizamos en emisor común de la forma más sencilla posible: Una fuente de alimentación de 10V colector-emisor. Una resistencia limitadora, R1, que calculamos para que la corriente de colector no supere 100mA. Una fuente de señal en la base, que podemos variar a voluntad. Cuando variemos Vin, hará variar la tensión de salida: Pasamos por las tres zonas características de un transistor bipolar: A la izquierda, el valor de Vin es demasiado bajo para activar la unión B-E y el transistor permanece inactivo, en corte. En el centro, la región activa. Como es un amplificador inversor la tensión de salida va bajando a medida que incrementamos la de entrada. A la derecha, el transistor ya está completamente abierto y la corriente de colector sólo está limitada por la resistencia R1. Ha llegado al valor máximo y apenas va a aumentar por mucho que aumente la corriente de base. Es la región de saturación. ¿Véis súbitamente cómo deja de amplificar? Nos interesa saber cómo varía la ganancia durante todo el recorrido anterior. Para eso representamos el cociente entre la tensión de salida y la de entrada. Decíamos que para que un amplificador no tuviera distorsión la ganancia tendría que ser la misma para todos los valores de entrada. Es evidente que no igual en todo el recorrido. Varía y mucho, luego nuestro amplificador va a distorsionar. La ganancia también puede variar con la temperatura o con el punto de trabajo... y esto en continua, pues en alterna depende también de la frecuencia; sin contar las capacidades parásitas o el efecto Early... si queréis indagar más sobre efectos no lineales os recomiendo este artículo: El transistor, ese gran desconocido. Salida con distorsión Aplicamos a la entrada una señal sinusoidal de 1000 Hz, centrada en 660 mV con una amplitud de 60 mV (es decir que irá desde los 600 mV a 720 mV). Según el gráfico anterior la tensión de salida es: Al menor valor de entrada, 600 mV -línea verde-, le corresponde una tensión de salida de casi 10 V. Es una amplificación de aproximadamente x16 (mirad la gráfica de la ganancia). Al mayor valor de entrada, 720 mV -línea roja- le corresponden 7 V. Una amplificación de algo menos de x10. Ahora viene lo bueno, si el máximo son 10 V y el mínimo 7 V, el valor medio es 8.5 V. Que debería corresponder con el valor medio de la entrada de 660 mV. Eso es lo que sucedería en un amplificador lineal bien diseñado. Pero NO en este. Al valor medio de la entrada le corresponden 9.5V -línea gris-. Está desplazado porque las amplitudes no se amplifican por igual. Por ese motivo aunque la entrada puede ser una sinusoidal (en rojo), la salida (en verde) podrá ser cualquier cosa: Electrónicamente ya hemos visto por qué se ha deformado la onda. Pero matemáticamente se podría explicar de esta forma: 1. La ganancia no era constante sino una función de la amplitud. 2. Cualquier función suave se puede aproximar por una serie de potencias al cuadrado, cubo, etc. 3. La señal de entrada -que era un seno- ha resultado multiplicada por un factor de amplificación y además elevada a distintas potencias. 4. Como ya hemos visto, elevar el seno a una potencia produce frecuencias múltiplos de la original: armónicos. 5. Los armónicos presentes a la salida deforman la onda (distorsionan). Y por supuesto tales frecuencias indeseadas se ven claramente en el espectro: Medida de la distorsión: la THD La Distorsión Armónica Total (DAT o más conocida como THD por sus siglas en inglés) es una magnitud que sirve para representar la calidad de un amplificador o de un oscilador. Mide la cantidad de armónicos no deseados presentes en la salida. Es decir si la señal de salida se parece mucho a la de entrada si es un amplificador, o a la que debería ser en caso de un oscilador (sinusoidal, cuadrada, etc). Se calcula aplicando a la entrada una señal de frecuencia y amplitud conocidas. Se suma la potencia de salida de todos los armónicos (basta con los diez primeros) y se divide la suma entre la potencia de salida de la frecuencia fundamental. El resultado se expresa casi siempre en porcentaje pero en ocasiones también podéis verlo en decibelios. Siempre que se da el dato de la THD, se debe indicar también para qué frecuencia y amplitud de entrada. Con LTSpice analizamos los diez primeros armónicos del circuito simple -gráfica anterior- y este es el resultado: Fourier components of V(out) DC component:8.97524 Harmonic Number 1 2 3 4 5 6 7 8 9 Frequency [Hz] 1.000e+03 2.000e+03 3.000e+03 4.000e+03 5.000e+03 6.000e+03 7.000e+03 8.000e+03 9.000e+03 Fourier Component 1.355e+00 4.667e-01 1.000e-01 2.281e-02 1.703e-02 1.488e-02 6.020e-03 8.213e-03 7.057e-03 Normalized Component 1.000e+00 3.445e-01 7.381e-02 1.684e-02 1.257e-02 1.098e-02 4.443e-03 6.062e-03 5.209e-03 Total Harmonic Distortion: 35.325777% Quiere decir que, un 35% de la potencia de salida se desperdicia en frecuencias no deseadas, distorsión. De toda la potencia entregada a la salida, sólo el 65% corresponde a la señal que queremos amplificar. Dicho de otra forma, la señal de salida sólo se parece en un 65% a la de entrada. Además, tiene una fuerte componente continua, de casi 9V que deberíamos filtrar. Tomemos ahora un amplificador bien diseñado como este preamplificador que viene de ejemplo en el LTSpice (se llama HandFreePreamp por si queréis buscarlo). Este esquema me gusta porque da muchas otras especificaciones técnicas que caracterizan un amplificador: La THD, indicando la frecuencia y la amplitud para la que se mide. En este caso 0.05% para 1 kHz con 0.4 Vpp de amplitud. El consumo y la tensión de alimentación. 1.9 mA. Una batería de 9 V tiene entre 400 y 570 mAh, así que 370 h de duración es aproximado y no para uso continuo. La ganancia en decibelios, así como la banda pasante a -3 dB. Este amplificador tiene una ganancia de 26.4 dB (x20) y se puede usar entre 38 Hz y 12 kHz. Más que suficiente para la voz. Para la música se queda un tanto corto en los agudos. La impedancia de salida y la frecuencia para la que se refiere. 387 Ω a 1 kHz. Es normal que no proporcionen la potencia de salida. Es un preamplificador, no lo olvidemos, y está pensado para conectarlo a un amplificador final de potencia. El ruido referido a la entrada. Un parámetro que no suelen darnos. Significa que en un amplificador exactamente igual sólo que sin ruido -ideal-, tendríamos que aplicar un ruido de 1.2 µV a la entrada para tener a la salida el mismo nivel de ruido que tenemos en silencio en el circuito real. El número de componentes de cada tipo. Si hacemos la misma gráfica que con el otro parece que no hay más frecuencias que la de entrada: Veamos qué sale en el análisis de Fourier: Fourier components of V(out) DC component:-0.000718343 Harmonic Number 1 2 3 4 5 6 7 8 9 Frequency [Hz] 1.000e+03 2.000e+03 3.000e+03 4.000e+03 5.000e+03 6.000e+03 7.000e+03 8.000e+03 9.000e+03 Fourier Component 2.017e-01 9.592e-05 2.369e-05 1.868e-05 1.495e-05 1.245e-05 1.067e-05 9.325e-06 8.283e-06 Normalized Component 1.000e+00 4.755e-04 1.174e-04 9.260e-05 7.410e-05 6.172e-05 5.287e-05 4.623e-05 4.106e-05 Total Harmonic Distortion: 0.051420% La THD es mucho mejor, un 0.05%. Evidentemente el 35% del otro circuito es una barbaridad. Como cabe esperar, en un amplificador bien diseñado la salida está centrada en cero, y los armónicos no son tan pronunciados como en el otro. En un gráfico con escala lineal como el de arriba no se aprecian pero sí en uno logarítmico. Mirad como el siguiente armónico, que es el tercero, está 25dB por debajo de la fundamental. Su amplitud es unas 20 veces menor.