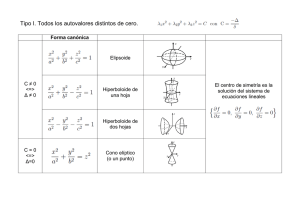
Paraboloide elíptico
Es la superficie que se ha creado al deslizar
una parábola vertical con la concavidad hacia
abajo a lo largo de la otra, perpendicular a la
primera. Las secciones horizontales de la
figura son elipses, mientras que las verticales
son parábolas.
Definición
Se denomina paraboloide elíptico a la superficie que en un sistema de coordenadas
cartesianas que se determina por la ecuación:
𝑥2 𝑦2
+
=𝑧
𝑎2 𝑏2
Las secciones de la cual son parabólicas o elípticas. El caso de revolución se obtiene
haciendo girar una parábola alrededor de su eje de simetría y resulta ser el lugar
geométrico de los centros de las esferas que pasan por un punto y son tangentes a
un plano.
Caracteristicas
El punto que coincide con el origen de coordenadas se llama vértice del paraboloide.
Si la figura no coincide con el origen de coordenadas en el vértice entonces la
ecuación es:
Las secciones que se obtienen al cortar la figura por planos con el eje Oz son
parábolas. Las secciones que se obtiene al corta la figura por planos con el eje Oz
son elipses.
Cuando a= b el paraboloide elíptico es un Paraboloide en Revolución.
Aplicación
Tiene la forma de las llamadas antenas parabólicas. Entre otros usos de origen
cotidiano. Tiene la propiedad de reflejar (en caso de tener una superficie reflactante)
la luz hacia un punto.
Procedimiento
Nuestra ecuación es igual a: 𝑧 = 𝑥 2 + 𝑦 2 − 16 por lo tanto es una paraboloide en
revolución.
𝑧 = 𝑥 2 + 𝑦 2 − 16
Z se convierte en 0
0 = 𝑥 2 + 𝑦 2 − 16
El radio al cuadrado es igual a x cuadrado más y cuadrado
𝑟2 = 𝑥 2 + 𝑦 2
Por lo tanto, nuestro radio será de:
𝑥 2 + 𝑦 2 = 16
𝑟 2 = 16
√𝑟 2 = √16
𝑟=4
Entonces el dominio de nuestra función es igual a:
Dominio= {x, y ≤ 4}
Y el rango serio:
Rango=z|-16≤ z ≤ ∞
Curvas de nivel
Ec1: 0 = 𝑥 2 + 𝑦 2
Ec9: 16 = 𝑥 2 + 𝑦 2
Ec2: 2 = 𝑥 2 + 𝑦 2
Ec10: 18 = 𝑥 2 + 𝑦 2
Ec3: 4 = 𝑥 2 + 𝑦 2
Ec11: 20 = 𝑥 2 + 𝑦 2
Ec4: 6 = 𝑥 2 + 𝑦 2
Ec12: 21 = 𝑥 2 + 𝑦 2
Ec5: 8 = 𝑥 2 + 𝑦 2
Ec6: 10 = 𝑥 2 + 𝑦 2
Ec7: 12 = 𝑥 2 + 𝑦 2
Ec8: 14 = 𝑥 2 + 𝑦 2