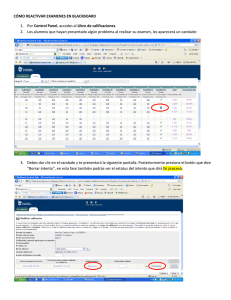
2 2 2 om Fig. 1: 1 + 2 + 3 = 14 2 2 2 2 Fig. 2: 1 + 2 + 3 + 4 = 30 2 2 2 2 2 Fig. 3: 1 + 2 + 3 + 4 + 5 = 55 2 2 2 2 2 2 Fig. 4: 1 + 2 + 3 + 4 + 5 + 6 = 55 + 36 = 91 2 2 2 2 2 2 2 Fig. 5: 1 + 2 + 3 + 4 + 5 + 6 + 7 = 91 + 49 = 140 --------------------------------------------PROBLEMA EXAMEN 2007 22. La policía detuvo a tres sospechosos del robo de un paquete. Al ser interrogados respondieron. Andrés: Bruno se llevó el paquete Bruno: Lo que dice Andrés es verdad Carlos: Yo no me llevé el paquete Si al menos uno de ellos mentía y al menos uno decía la verdad. ¿Quién robó el paquete? A. Carlos B. Andrés C. Bruno D. No se pudo determinar --------------------------------------------SOLUCION 22. RESPUESTA: B Analizando: Andrés: Bruno se llevó el paquete Bruno: Lo que dice Andrés es verdad Carlos: Yo no me llevé el paquete. Las afirmaciones de Andres y Bruno estan relacionadas, es decir no entran en contradicción si se dice la verdad. Si Andres dice la verdad: Andrés: Bruno se llevó el paquete (V) Bruno Lo que afirma deberia ser Verdadero (V) Carlos Si Bruno robo, Carlos estaria diciendo la verdad Como uno miente, no es posible que Andres diga la verdad. Entonces: Andres miente. Andrés: Bruno se llevó el paquete (F) Entonces Bruno "no se llevo el paquete" Bruno: Lo que dice Andrés es verdad (F) Como es falso: Bruno no robo. Carlos: Yo no me llevé el paquete. (V) Por lo menos uno dice la verdad. Como: Bruno no robo y Carlos no robo. La unica posibilidad es que robo: Andres. --------------------------------------------PROBLEMA EXAMEN 2007 w w w .M at em at 23. Hay 70 bolitas en una caja: 20 de ellas son rojas, 20 son verdes, 20 son amarillas y de las restantes algunas son negras y otras son blancas. Al menos ¿cuántas bolitas debemos sacar de la caja, sin mirarlas para tener la seguridad de que entre estas habrá 10 bolitas del mismo color? A) 35 B) 36 C) 37 D) 38 E) 39 --------------------------------------------SOLUCION 23. RESPUESTA: D En este tipo de problemas para tener la certeza de obtener lo que se busca se debe asumir el peor de los casos. En la bolsa hay: 20 rojas, 20 verdes, 20 amarillas y 10 (negras y blancas) Casos: 9 rojas + 1 verde 9 rojas + 9 verdes + 9 amarillas 9 rojas + 9 verdes + 9 amarillas + 10 (negras y blancas) En este caso si sacamos una bolita mas esta debe ser necesariamente de color: rojo, verde o amarillo. Nota: Las bolitas negras o blancas nunca llegan a completar 10 del mismo color. Para obtener 10 bolitas del mismo color: 9 rojas + 9 verdes + 9 amarillas + 10 (negras y blancas) + 1 = = 38 bolitas Al sacar 38 bolitas hay la seguridad que 10 sean del mismo color. --------------------------------------------PROBLEMA EXAMEN 2006 .c --------------------------------------------PROBLEMA EXAMEN 2006 a1 DE LA CARRERA PUBLICA MAGISTERIAL A) 100 B) 91 C) 204 D) 140 E) 271 --------------------------------------------SOLUCION 34. RESPUESTA: D Se observa, que las bases son cubitos que forman un 2 cuadrado de lados (n)(n) = n : ic PROBLEMAS DE RAZONAMIENTO LOGICO 28. Un libro de lenguaje y uno de matematica cuestan en total S/. 28. Además se sabe que tres libros de rnatemática cuestan lo mismo que cuatro libros de lenguaje. ¿Cuánto costará un libro de lenguaje? A) S/.18 B) S/. 16 C) S/.12 D) S/. 14 E) S/.10 --------------------------------------------SOLUCION 28. RESPUESTA: C Se sabe que tres libros de rnatemática cuestan lo mismo que cuatro libros de lenguaje: 3 M = 4 L Si un libro de lenguaje cuesta "3x" entonces un libro de matematica cuesta: "4x". En total un libro de lenguaje y uno de matematica cuestan 28 soles, entonces: 3x + 4x = 28 7x = 28 28 x= 7 x=4 Un libro de Lenguaje cuesta 3x = 3(4) = 12 soles --------------------------------------------PROBLEMA EXAMEN 2006 34. Las figuras muestras una secuencia de sólidos formados pr cubos siguiendo la misma secuencia ¿cuántos cubos tendría el solido de la figura 5? 24. Un testigo de un asalto, informó a la policia que el auto utilizado por los ladrones para la fuga tenía una placa de 4 símbolos: los dos primeros eran vocales y los dos últimos eran dígitos mayores que seis. ¿Cuántos autos deberá investigar la policía? A) 16 B) 125 C) 225 D) 400 --------------------------------------------SOLUCION 24. RESPUESTA: C Las vocales pueden ser: A; E; I; O; U Los digitos mayores que 6 son: 7; 8 y 9 Por teoria de combinaciones: 32) Se tiene cuatro candados A, B, C y D; y dos llaves X e Y. Si cada llave abre solo un candado, ¿cual es el número de veces que las llaves deben insertarse en los candados para saber con certeza cual es la llave que abre cada candado? A. 5 B. 6 C. 7 D. 8 --------------------------------------------SOLUCION 32. RESPUESTA: A Analizando en el caso de 2 candados y 1 llave, solo es necesario probar una sola vez, puesto que si no abre en el Intento 1, la llave pertenece al segundo candado. Intento 1 Descartado --------------------------------------------PROBLEMA EXAMEN 2007 25. Al elaborar pastelillos, el 5% de la fruta comprada se desperdícia. Si para un pedido de pasteles se necesita 190 kg. netos de fruta, ¿cuántos kg. se debe comprar? Candado 2 Candado 2 Candado 3 co m Candado 1 ic a1 . Para el problema tenemos: 4 candados y 2 llaves. Analizamos el peor de los casos con la llave "X": Intento 1 Intento 2 Intento 3 Descartado w w .M at em at A) 199,5 B) 190,5 c C) 195 D) 200 --------------------------------------------SOLUCION 25. RESPUESTA: D Método 1: Sea "x" el total de fruta comprada x = (desperdicio) + (consumo neto) x = 5%(x) + 190 5 ( x ) + 190 x= 100 5 x( x ) = 190 100 100 x 5 x = 190 100 95 x (190 )(100 ) = 190 x = = 200 kg 100 95 Método 2: Si se desperdicia el 5% se utiliza el 95% neto de la fruta. 190 kg = 95% (Total de fruta) 95 (Total de fruta) 190 kg = 100 (190 )(100 ) (Total de fruta) = kg 95 (190 )(100 ) Total de fruta = kg 95 Total de fruta = 200 kg --------------------------------------------PROBLEMA EXAMEN 2007 Candado 1 En el caso de 3 candados, solo es necesario hacer 2 intentos, puesto que si no abre en el segundo intento la llave por descarte pertenece al tercer candado. Intento 1 Intento 2 Descartado w Candado 1 Candado 2 Candado 3 Candado 4 Si en el intento 3, la llave "X" no abre el candado 3, la llave "X" por descarte debe de abrir el candado 4, no es necesario intentar abrir. Solo se hace 3 intentos. Ahora nos queda probar 3 candados con la llave Y: Intento 1 Intento 2 Descartado 31. Martina tiene varias cuentas de ahorro en distintos bancos de la ciudad. Si deposita S/. 200 en cada una de tres de ellas y retira S/. 120 de cada una de cinco de sus cuentas, ¿En cuántos soles varió su capital?. A) Aumentó en 80 nuevos soles B) Disminuyó en 80 nuevos soles C) Aumentó en 20 nuevos soles D) No varió --------------------------------------------SOLUCION 31. RESPUESTA: D Deposita: (200)(3) = 600 soles Retira: (120)(5) = 600 soles Deposito = Retiro No varió Nota: Como hay 5 cuentas se supone que en un banco "puede" tener 2 o mas cuentas; ejemplo: si en un banco deposita 200; en este banco puede tener 2 cuentas una de 120 y otra de 80. --------------------------------------------PROBLEMA EXAMEN 2007 - 22 ENERO Candado 1 Candado 2 Candado 3 En el peor de los casos se hace 2 intentos, si la llave "Y" no abre el candado 2 por descarte la llave "Y" debe de abrir el candado 3. Se hace 2 intentos. En total se hace 3 + 2 = 5 intentos --------------------------------------------PROBLEMA EXAMEN 2007 - 22 ENERO 36) El sólido mostrado esta formado por 27 cubitos de 3 1cm , si se pintan de rojo cinco caras de este sólido, ¿cuantos cubitos tendrán solo una cara pintada? A. 5 B: 8 C: 6 D. 9 2 --------------------------------------------SOLUCION 36. RESPUESTA: Como el cubo tiene 6 caras y se pintan 5, quedaria una cara sin pintar, distinguimos los cubitos con una cara pintada y con dos caras pintadas: --------------------------------------------SOLUCION 31. RESPUESTA: C Se observa que todas las filas y columnas tienen siempre una combinacion de tres figuras en la parte central: triangulo, cuadrado y circulo. En la cara que queda sin pintar reconocemos 4 cubitos que tienen solo una cara pintada: a1 ic w .M at em at En cada cara pintada reconocemos un cubito pintado una sola cara que corresponde al cubito central, como son 5 caras pintadas hay 5 cubitos más: .c om Además observamos (por filas y columnas) que la suma de puntos que lleva las figuras con cuadrado y circulo resulta la cantidad de puntos que lleva la figura con triangulo. Fila 1: w w Puntos en la figura con cuadrado: 3 Puntos en la figura con círculo: 2 Suma: 3 + 2 = 5 Puntos en la figura con triangulo: 5 Nota: 2 figuras tienen los puntos dentro del círculo y 1 figura los puntos fuera del círculo. Fila 2: Total: 4 + 5 = 9 --------------------------------------------PROBLEMA EXAMEN 2008 - 9 MARZO 31. Indicar la figura que falta: Puntos en la figura con cuadrado: 1 Puntos en la figura con círculo: 2 Suma: 1 + 2 = 3 Puntos en la figura con triangulo: 3 Nota: 2 figuras tienen los puntos dentro del círculo y 1 figura los puntos fuera del círculo. Fila 3: Puntos en la figura con cuadrado: 3 Puntos en la figura con círculo: 0 Suma: 3 + 0 = 3 Puntos en la figura con triangulo: 3 Nota: 2 figuras tienen los puntos dentro del círculo, la figura que sigue debe tener los puntos fuera del círculo. 3 SOLUCION La figura que debe seguir es una que tenga en la parte central un triangulo con 3 puntos y estos puntos deben estar fuera del círculo. 49. RESPUESTA: B Del dato: Dividiendo entre 2: 6 2 = 4 2 Multiplicando por 5: 6 3 5(3 =4 =2 ) = 5(2 15 = 10 Del segundo dato: 5 =4 Multiplicando por 2: 2(5 ) = 2(4 10 =8 Sigue C: De () y (): ic a1 .c om --------------------------------------------PROBLEMA EXAMEN 2010 - 8 AGOSTO w w w .M at em at --------------------------------------------27. RESPUESTA: A Se completa con A: --------------------------------------------PROBLEMA EXAMEN 2010 - 8 AGOSTO --------------------------------------------32. RESPUESTA: D (5)(4)+1 = 21 ; (6)(2)+1 = 13 ; (3)(7)+1 = 22 --------------------------------------------PROBLEMA EXAMEN 2010 - 22 AGOSTO A.10 B.8 C.6 D.9 --------------------------------------------- 4 15 = 10 =8 ) .....................() ) ....................()