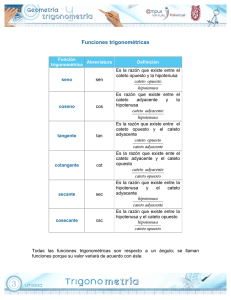
Matemáticas II ACTIVIDADES SEMANA 2 TEMA 1. TRIANGULOS OBLICUANGULOS Para medir una distancia o la altura de un objeto, como por ejemplo, medir la altura de un árbol a partir del ancho de la carretera y con dos ángulos de elevación conocidos, como se muestra en la figura 8.4, es necesario recurrir a las leyes de senos y cosenos. Otra de las aplicaciones de estas dos leyes es en la construcción, específicamente en la topografía, cuando se está midiendo el perímetro de un terreno de forma irregular, el ancho de un río, la altura de una barranca y no es posible la medición de forma directa. En estos casos podemos emplear triángulos oblicuángulos para hallar la medida de forma indirecta. Ley de senos La ley de senos es una relación de tres igualdades que siempre se cumplen entre los lados y ángulos de un triángulo oblicuángulo cualquiera. Esta ley es la razón entre la longitud de cada lado y el seno del ángulo opuesto a él. ACTIVIDAD 1- Realiza un ejemplo de ley de senos, aplicando la formula, triangulo y su desarrollo. TEMA 2. APLICACIÓN EN LA VIDA COTIDIANA DE SENOS Y COSENOS. Producto de aprendizaje: construcción de una maqueta: determinación de la distancia entre dos barcos por el vigía del faro Instrucciones: Los faros marítimos son puntos estratégicos en las costas de los océanos y mares. Tienen la tarea de prevenir accidentes con los barcos, por una parte para que no choquen contra los arrecifes y, por otra para, que no choquen entre ellos por las noches. Construye una maqueta en donde representen un faro (punto de observación del vigía), el mar, así como la posición relativa de dos barcos. Demuestra cómo el vigía puede determinar la distancia entre los barcos aplicando la ley de senos o cosenos. Determinen la distancia a cada uno de ellos y el ángulo de separación entre los barcos desde el faro. Finalmente, escribe en media hoja una reflexión con sus propias palabras sobre la importancia de usar la ley de los senos o cosenos en el contexto laboral. Cuida que tus ideas sean coherentes y escribe sin errores ortográficos. Utiliza cualquier tipo de material que tengas en casa. TEMA 3. IDENTIDADES TRIGONOMETRICAS Las identidades trigonométricas son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones. Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas utilizaremos estas técnicas en conjunto con las identidades trigonométricas. ACTIVIDAD 3- RESPONDE A LAS SIGUIENTES PREGUNTAS. 1. Las funciones trigonométricas vienen del estudio de un triángulo rectángulo, y cada una de las razones a saber de dicho estudio dependen del valor de: a) Las medidas de sus lados b) Los ángulos del triángulo.. c) La distancia hacia el lado opuesto d) La longitud de la hipotenusa 2 . EL SENO en un triángulo rectángulo e define como: a) La longitud del cateto opuesto al ángulo entre la longitud de la hipotenusa.. b) La longitud del cateto adyacente al ángulo entre la hipotenusa c) La longitud del cateto opuesto entre la longitud del cateto contiguo d) La longitud de la hipotenusa entre el cateto opuesto. 3 La razón inversa de la SECANTE de un ángulo es: a) La tangente del ángulo b) El coseno del ángulo c) El seno del ángulo.. d) La cosecante del ángulo 4 En un triángulo rectángulo al dividir el cateto opuesto y la adyacente nos daría la función de: SUSTENTE a. La cosecante del ángulo b. El coseno del ángulo c. El seno del ángulo d. La tangente del ángulo.. 5 La circunferencia que tiene su centro e el origen de las coordenadas y su radio es la unidad y además los ejes de coordenadas delimitan cuatro cuadrantes se llama: SUSTENTE a. Radiométrica b. Circunmétrica c. Goniométrica.. d. Geométrica 6 Si el ángulo de elevación del sol es de 31 grado, la longitud de la sombra proyectada por un hombre que tiene 180 cm de estatura es de: SUSTENTE a. 3. Metros…. b. 4. metros c. 2. metros. d. 5. Metros 7 . Al calcular el ´área de un dodecágono regular cuyo lado mide 6 cm se obtiene: SUSTENTE a. 408.13 cm b. 403.13 cm.. c. 413.53 cm d. 453.53 cm 8 Sabemos que en un triangulo rectángulo un cateto mide 10 cm y el ángulo opuesto a dicho cateto tiene coseno de 0.4 al calcular la longitud del otro cateto y la hipotenusa el resultado es: SUSTENTE a. Cateto 5,36 cm hipotenusa 12.91 cm² b. Cateto 3.36 cm.. hipotenusa 11.11 cm² c. Cateto 4,36 cm hipotenusa 10.91 cm².. d. Cateto2.36 cm.. hipotenusa 9,91 cm² BIBLIOGRAFIA: https://www.dgb.sep.gob.mx/servicios-educativos/telebachillerato/LIBROS/2-semestre2016/Matematicas-II.pdf http://richardiny.blogspot.com/2012/08/cuestionario-funciones-trigonometricas.html Telebachillerato Comunitario Segundo Semestre Matemáticas II Secretaría de Educación Pública Aurelio Nuño Mayer Subsecretaría de Educación Media Superior Rodolfo Tuirán Gutiérrez Dirección General del Bachillerato Carlos Santos Ancira