FUNCIONES TRIGONOMÉTRICAS Determinación de las

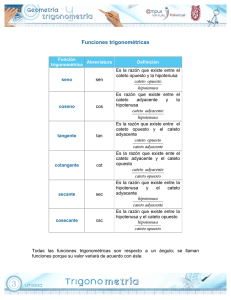
FUNCIONES TRIGONOMÉTRICAS
Determinación de las funciones seno, coseno y tangente de los ángulos de 30° y
60°
Para las funciones de los ángulos de 30° y 60° Part imos de un triángulo equilátero
de de lado 1.
30°
1
1
1
1
90°
1
1
2
60°
1
2
Muy bien ahora tenemos dos triángulos rectángulos, analicemos uno de ellos.
sen..x =
cateto..opuesto
hipotenusa
tan ..x =
cos ..x =
cateto..adyascente
hipotenusa
cateto..opuesto
cateto..adyascente
Para el ángulo de 30° el cateto opuesto mide
1
, el cateto adyacente es igual a la
2
altura del triángulo y la hipotenusa mide 1.
Determinemos la altura del triángulo:
2
1
Por teorema de Pitágoras la altura será a = c − b , es decir a = 1 −   ,
2
2
haciendo operaciones nos queda: a = 1 −
3
3
=
4
2
1
=
4
2
2
3
, es decir la altura mide:
4
FUNCIONES TRIGONOMÉTRICAS
Continuamos con las funciones trigonométricas.
3
cos ..30° = 4 =
1
1
1
Entonces sen..30° = 2 =
1 2
1
1
1
tan .30° = 2 = 2 =
3
3
3
4
2
3
3
=
4
2
Para el ángulo de 60°, el cateto opuesto mide la al tura del triángulo
adyacente mide
Entonces:
3
, el cateto
4
1
y la hipotenusa mide 1
2
3
sen..60° = 4 =
1
3
3
=
4
2
1
1
cos ..60° = 2 =
1 2
3
3
3 1
3
tan ..60° = 4 = 2 =
÷ =
= 3
1
1
2 2
1
2
2
Estos los valores exactos de las funciones trigonométricas de los ángulos vistos.
30°
60°
Seno
1
2
3
3
=
4
2
Coseno
3
3
=
4
2
1
2
Tangente
1
3
3
Valores aproximados, obtenidos mediante tablas o con calculadora.
Seno
30° 0.5
60° 0.5
Coseno
0.866
0.5
Tangente
0.5773
1.7320
Mtro. Marco Antonio Serrano Moreno