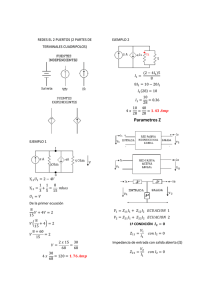
PROBLEMA Se tiene el circuito mostrado de la figura, se conoce que la impedancia equivalente total es 20/3 ohmios puramente resistiva, evaluar los valores de X C y XL para que el circuito cumpla en ser puramente resistivo. Calcularemos los valores de XC y XL a través de las ecuaciones de admitancias. En primer lugar juntaremos en una sola admitancia los valores de las impedancias que no sean variables: 1 1 5 J 5 J 20 1 J YF 10 20 La admitancia equivalente es: YF Y EQ Y F Y C Y L …(α) Ahora por dato: Y EQ 30º 20 Ahora trabajando en (α): 30º 2 1 1 1 …(β) J 20 20 JX C 10 JX L 20 Luego si trabajamos en el gráfico de las admitancias: En el grafico elegimos un caso particular de resonancia ya que no nos dan los valores de “L” ni “C”, pero nos dan el valor de la admitancia total, entonces si trabajamos con esa condición el grafico seria el siguiente: Ahora si reemplazamos estos nuevos datos a la ecuación β, por lo tanto los valores de XC y XL son: 1 1 X C 10 X C 10 1 1 1 J 10 JX L 20 20 20 10 1 J XL X L 10 J Problema.- A dos ramas paralelas se le aplican 120 voltios a cero grados Z1 1590 y Z 2 consiste en una resistencia de 5 ohmios en serie con una reactancia capacitiva que varía de cero al infinito, encontrar (solo aceptable análisis gráfico), la corriente mínima y el f.d.p correspondiente…. Y el f.d.p mínimo para la corriente en adelanto. (Ver figura). SOLUCION: En la resolución de este problema hay que trabajar a escala por lo tanto hay que ser muy minuciosos en la solución: Análisis matemático: YT Y1 Y2 YT 1 1 J 15 (5 JX C ) YT Racionalizando tenemos: 5 JX C J 15 (25 X C 2 ) YT XC 5 1 ( )J 2 2 (25 X C ) 25 X C 15 Para que existirá resonancia en el circuito tendríamos la parte imaginaria a cero de lo cual hallaremos para que valores existe dicha resonancia : Im a _ YT 0 ( XC 1 )0 2 25 X C 15 X C 15 X C 25 0 2 X C1 1.909 y Hallando obtenemos: X C 2 13.095 Por lo tanto afirmamos que para estos valores de reactancia de la capacitancia el circuito resuena. Ahora bien trabajemos con las corrientes: Tenemos: V I1 X L I1 1200 8 90 15 J Para I 2 hacemos que X C 0 por lo tanto la corriente será máxima. 1200 240 Por lo tanto concluimos que la corriente I 2 variara de 5 acuerdo a X C y el lugar geométrico descrito será una media circunferencia así: I2 I T min ima IT max ima Fig. (Sin escala) Del gráfico: tan 8 8 33.69 tan 18.43 12 24 Por cálculos tenemos: Para hallar ITmin hallamos I2min para lo cual mediante ley de cosenos tenemos: X 2 12 2 12 2 2(12)(12) cos(33.69) X 2 48.369 X 6.954 Luego la corriente I2 seria I 2min 6.95473.155 I Tmin I 1 I 2 min 8 90 6.95473.155 2.4224 33.708 El f.d.p viene dado por: cos( 33.708) 0.83187 Para la segunda pregunta donde nos indica que la corriente adelanta (respecto a la tensión) y el f.d.p mínimo para resolver analizamos el lugar geométrico a escala para tener mayor precisión en los datos. I1 8 90 I 2 240......Cuando.. X c 0 FIG (CON ESCALA 1:1) 14 ,12 ° 54 22° 21° 45° 50° ° 54 ° 57 ° 60 ° 68 ° 69 1 97 , 6 34 22, Para estos valores mostrados en la gráfica hacemos una tabla y hay q ver cuales el f.d.p mínimo. item 1 2 3 4 5 6 7 8 21° 35° 45° 50° 52° 54° 57° 60° I T (Corriente...total) K 20.8560.016 18.2377.673 12.64818.433 10.63721.091 9.82021.898 8.97722.414 7.62722.163 6.43521.572 f .d . p cos( ) 0.9910 0.99104 0.94869 0.93301 0.92784 0.92445 0.92611 0.92995 Como observamos el f.d.p mínimo es (0.92445) cuando la corriente es: I 2 14.1254 para que la corriente este en adelanto.