000125726

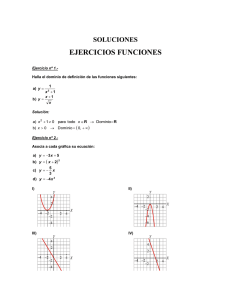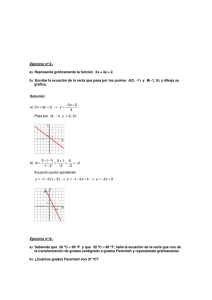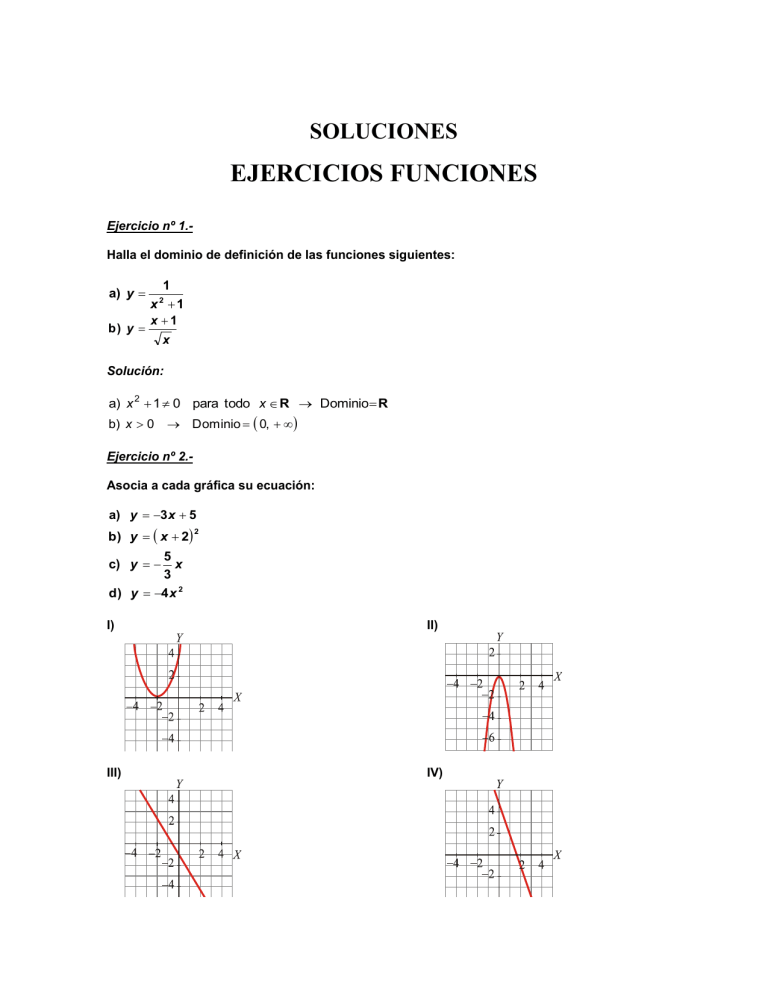
SOLUCIONES
EJERCICIOS FUNCIONES
Ejercicio nº 1.Halla el dominio de definición de las funciones siguientes:
a) y 
b) y 
1
x 1
x 1
2
x
Solución:
a) x 2  1  0 para todo x  R  Dominio R
b) x  0
 Dominio   0,   
Ejercicio nº 2.Asocia a cada gráfica su ecuación:
a) y  3 x  5
b) y   x  2
2
5
x
3
d) y  4 x 2
c) y  
I)
II)
III)
IV)
Solución:
a)
b)
c)
d)
IV
I
III
II
Ejercicio nº 3.Representa la gráfica de la siguiente función:
y 
3
x 1
5
Solución:
Ejercicio nº 4.Halla la expresión analítica de la recta cuya gráfica es:
Solución:
Observ amosque la rectapasa por los puntos  0, 20 y
m
80  20 60 6


50  0
50 5
Por tanto, su ecuación es:
y
6
x  20
5
 50, 80. Su pendiente será:
Ejercicio nº 5.Representa la gráfica de la siguiente función:
y  x 2  4
Solución:
 El v érticede la parábola está en
 0, 4 .
 Puntos de corte con los ejes:
2
Con el eje X  y  0   x  4  0

x2  4

 x   4   2  Puntos   2, 0 y  2, 0
Con el eje Y 
x0

y 4
 Punto  0, 4
 Hallamos algún otro punto:
 La gráfica es
Ejercicio nº 6.Representa gráficamente:
 2 x  1 si x  1
y  2
si x  1
x  2
Solución:
Si x  1, tenemosun trozo de recta.
Si x  1, es un trozo de parábola.
La gráfica es:
Ejercicio nº 7.Con 200 metros de valla queremos acotar un recinto rectangular aprovechando una pared:
a) Llama x a uno de los lados de la valla. ¿Cuánto valen los otros dos lados?
b) Construye la función que nos da el área del recinto.
Solución:
a)
b) Área  x200  2x   200x  2x 2
Ejercicio nº 8.Haz la gráfica de la función:
y  0,5x  3,5
Solución:
Ejercicio nº 9.-
Hallala ecuaciónde la recta quepasa por  1, 2 y cuya pendientees 
Solución:
Escribimos la ecuación puntopendiente:
1
.
3
y 
1
x  1  2
3
Operando, llegamos a:
1
1
1
5
x 2
x
3
3
3
3
1
5
y 
x
3
3
y 
Ejercicio nº 10.Representa gráficamente la siguiente función:
f x   2 x 2  4 x
Solución:
 El vértice de la parábola es:
x
b 4

1 
2a  4
y 2

Punto  1, 2
 Puntos de corte con los ejes:
Con el eje X  y  0  2x 2  4x  0  x  2x  4  0
x  0

 2 x  4  0
Con el eje Y 
x 0

 Hallamos algún otro punto:
 La gráfica es:


y 0
Punto  0, 0 
x  2  Punto  2, 0 
 Punto  0, 0
Ejercicio nº 11.Dibuja la gráfica de la función:
 x  1/2
y 
2
 x
si x  1
si x  1
Solución:
Si x ≤ -1, es un trozo de recta.
Si x > -1, es un trozo de parábola.
La gráfica es:
Ejercicio nº 12.Un cántaro vacío con capacidad para 20 litros pesa 2550 gramos. Escribe la función que nos
da el peso total del cántaro según la cantidad de agua, en litros, que contiene.
Solución:
El peso del cántaro vacío es de 2,55 kg. Si echamos x litros de agua, pesará x kg más, es decir,
la función que buscamos es:
y  2,55  x
donde x e y están en kilos. Además, x varía entre 0 y 20, es decir, 0  x  20.
Ejercicio nº 13.Halla el dominio de definición de las siguientes funciones:
a) y 
1
x 9
2
b) y  x  2
Solución:
a) x 2  9  0 
b) x  2  0

x2  9 
x2
x   9  3  Dominio  R   3, 3
 Dominio  2,  
Ejercicio nº 14.Obtén la gráfica de la función:
f x  
x2
 2x  1
2
Solución:
 Hallamos el vértice de la parábola:
b 2
  2  y  1  Punto  2,  1
2a 1
 Puntos de corte con los ejes:
x2
Con el eje X  y  0 
 2x  1  0 
2
x
x
Con el eje Y 
4  16  8
2
x0


 x  3,41


x  0,59

Punto  3,41; 0

Punto  0,59 ; 0
y  1  Punto  0, 1
 Hallamos algún otro punto:
 La gráfica es:
f (x) 
x2
 2x  1
2
Ejercicio nº 15.Representa la siguiente función:
 2
y  2 x
2 x  4
si
si
Solución:
Si x < -1, tenemos un trozo de parábola.
Si x ≥ -1, tenemos un trozo de recta.
La gráfica es:
x 2  4x  2  0
x  1
x  1
Ejercicio nº 16.El perímetro de un rectángulo es de 30 cm. Obtén la función que nos dé el área del
rectángulo en función de la longitud de la base.
Solución:
Llamamos x a la longitud de la base.
Si el perímetro es de 30 cm, la altura será 15  x.
Por tanto, el área es:
A  x 15  x   15x  x 2
Ejercicio nº 17.Halla el dominio de definición de las funciones:
a) y 
2x
x2
b) y  3 x  1
Solución:
a) x 2  0

b) 3 x  1  0
x0

 Dominio  R   0
3x  1 
x 
1
3

1

Dominio   ,   
3


Ejercicio nº 18.Dibuja la gráfica de la siguiente función:
si x  1
 x 2
y 

x

1
2
si x  1

Solución:
Son dos trozos de recta.
La gráfica es:
Ejercicio nº 19.El precio por establecimiento de llamada en cierta tarifa telefónica es de 0,12 euros. Si
hablamos durante 5 minutos, la llamada nos cuesta 0,87 euros en total. Halla la función que
nos da el precio total de la llamada según los minutos que estemos hablando.
Solución:
La función que buscamos será de la forma:
y  0,12  m · x,
donde x son los minutos que estamos hablando.
Para hallar el valor de m tenemos en cuenta que:
x  5  0,87  0,12  m  5
Así, la función es:

m  0,15
y  0,12  0,15x
Ejercicio nº 20Averigua cuál es el dominio de definición de las siguientes funciones:
a) y 
1
3x  x 2
b) y  x 2  1
Solución:
a) 3 x  x 2  0

x  0
x 3  x   0 
 Dominio  R  0, 3
x  3
b) x 2  1  0  Dominio   ,1  1,
Ejercicio nº 21.Asocia a cada una de estas gráficas una de las siguientes expresiones analíticas:
 3x 2
a) y 
4
3 x
b) y 
4
c) y  2 x 2  2
d) y  2 x  2
I)
II)
III)
IV)
Solución:
a)
b)
c)
d)
II
I
IV
III
Ejercicio nº 22.Representa gráficamente la función:
y  x 2  4x  1
Solución:
 Hallamos el vértice:
b 4

2  y 3
2a  2
 Puntos de corte con los ejes:
x
 Punto  2, 3.
Con el eje X  y  0   x 2  4x  1  0 

Con el eje Y 
 4  12  x  0,27

2
 x  3,73
x0

 Hallamos algún otro punto:


x
 4  16  4

2
Punto  0,27 ; 0
Punto  3,73 ; 0 
y  1  Punto  0,  1
 La gráfica es:
Ejercicio nº 23.Representa gráficamente la siguiente función:
 2
y   x  1 si
si
3
x 2
x 2
Solución:
Si x ≤ 2, es un trozo de parábola.
Si x > 2, es un trozo de recta horizontal.
La gráfica es:
Ejercicio nº 24.En algunos países se utiliza un sistema de medición de la temperatura distinto a los grados
centígrados que son los grados Farenheit. Sabiendo que 10 C  50 F y que 60 C  140 F,
obtén la ecuación que nos permita traducir temperaturas de C a F.
Solución:
Llamamos x a la temperatura en grados centígrados e y a la temperatura en grados Farenheit.
La función que buscamos pasa por los puntos (10, 50) y (60, 140). Será una recta con pendiente:
m
140  50 90 9


60  10
50 5
La ecuación es:
9
x  10  50  9 x  18  50  9 x  32
5
5
5
9
y  x  32
5
y 