Unidad4 act15 Excendete del consumidor y del productor MaricruzLandeta

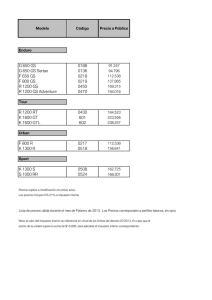
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE COMERCIO Y ADMINISTRACIÓN
UNIDAD SANTO TOMÁS
MATEMÁTICAS PARA NEGOCIOS
Asesor: Ing. Leopoldo Javier Hernández
Portafolio de evidencias
Alumna: Landeta Ortega Maricruz
Grupo: 1RX14
Actividad 15: Excedente del consumidor y del productor.
Problema.
Se conocen las funciones:
𝑝 = 1200 − 1.5𝑥 2
𝑝 = 200 + 𝑥 2
Se pide:



Calcular el punto de equilibrio.
Calcular el excedente del productor.
Calcular el excedente del consumidor.
Solución:
a. Calculando el punto de equilibrio (𝑞0 , 𝑝0 ), igualaremos ambas funciones para
despejar x:
1200 − 1.5𝑥 2 = 200 + 𝑥 2
2.5𝑥 2 = 1000
𝑥2 =
1000
2.5
𝑥 = √400 = 20 𝑠𝑒𝑟á𝑛 𝑙𝑎𝑠 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠 𝑝𝑟𝑜𝑑𝑢𝑐𝑖𝑑𝑎𝑠
Sustituimos x en cualquiera de las dos funciones:
𝑝 = 200 + 𝑥 2 = 200 + (20)2 = 200 + 400 = 600 𝑠𝑒𝑟á 𝑒𝑙 𝑝𝑟𝑒𝑐𝑖𝑜
El punto de equilibrio es (20,600)
*Comprobación*
𝑝 = 1200 − 1.5(20)2 = 1200 − 1.5(400) = 1200 − 600 = 600
𝑝 = 200 + 𝑥 2 = 200 + (20)2 = 200 + 400 = 600
Adaptamos q en lugar de x en ambas funciones:
𝑑(𝑞) = 1200 − 1.5𝑞 2
𝑓(𝑞) = 200 + 𝑞 2
b. Calcular el excedente del productor.
Usando la fórmula:
𝑞0
𝑒𝑝 = 𝑝0 𝑞0 − ∫ 𝑓(𝑞)𝑑𝑞
0
20
20
𝑒𝑝 = (20)(600) − ∫ (200 + 𝑞
2 )𝑑𝑞
0
= 12000 − 4000 −
𝑞3
= 12000 − [200𝑞 + ]
3 0
8000
8000
= 8000 −
3
3
𝑒𝑝 = 5333.33 𝑠𝑒𝑟á 𝑒𝑙 𝑒𝑥𝑐𝑒𝑛𝑑𝑒𝑛𝑡𝑒 𝑑𝑒𝑙 𝑝𝑟𝑜𝑑𝑢𝑐𝑡𝑜𝑟
c. Calcular el excedente del consumidor.
Usando la fórmula:
𝑞0
𝑒𝑐 = −𝑝0 𝑞0 + ∫ 𝑑(𝑞)𝑑𝑞
0
20
𝑒𝑐 = −(20 ∙ 600) + ∫ (1200 − 1.5𝑞 2 )𝑑𝑞 = −12000 + [1200𝑞 − 0.5𝑞 3 ]20
0
0
𝑒𝑐 = −12000 + 24000 − 4000 = 8000 𝑠𝑒𝑟á 𝑒𝑙 𝑒𝑥𝑐𝑒𝑑𝑒𝑛𝑡𝑒 𝑑𝑒𝑙 𝑐𝑜𝑛𝑠𝑢𝑚𝑖𝑑𝑜𝑟