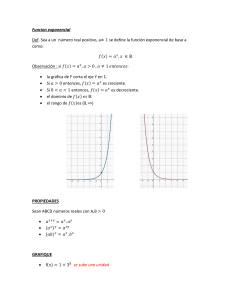
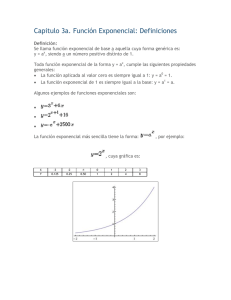
UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL FUNCION EXPONENCIAL Las funciones exponenciales son funciones en las cuales la variable independiente está en la posición del exponente. DEFINICIÓN: Sea x cualquier número real. La función exponencial base a es una función de la forma 𝑓(𝑥) = 𝑎 𝑥 , donde a es un número real positivo (𝑎 > 0) 𝑦 𝑎 ≠ 0. OBSERVACIÓN: No se incluye la base a = 1, porque si a = 1 entonces tendríamos la función constante 𝑓(𝑥) = 1𝑥 = 1 CUIDADO: Es importante distinguir entre la función 𝑓(𝑥) = 𝑥 2 , la cual es una función polinomial de grado 2 y la función 𝑔(𝑥) = 2𝑥 , la cual es una función exponencial de base 2. En una función polinomial, la base es una variable y el exponente es una constante. En una función exponencial, la base es una constante y el exponente es una variable. GRÁFICAS DE FUNCIONES EXPONENCIALES Para graficar este tipo de funciones tenemos que tener en cuenta que el dominio es el conjunto de números reales. Este tipo de funciones solo presenta una asíntota del tipo horizontal. ASÍNTOTA HORIZONTAL La asíntota horizontal es una recta horizontal a la cual la gráfica de la función se va acercando cuando los valores en el dominio de la función aumentan o disminuyen. Si la gráfica de la función tiene esta asíntota, entonces ella nos describe el comportamiento al final de la gráfica. Las asíntotas ayudaran en la construcción de la gráfica, la trazaremos con una línea discontinua. APLICACIÓN DE UNA FUNCION EXPONENCIAL La función exponencial se presenta en multitud de fenómenos de crecimiento animal, vegetal, económico, etc. En todos ellos la variable es el tiempo. En el crecimiento exponencial, cada valor de y se obtiene multiplicando el valor anterior por una cantidad constante a. Donde k es el valor inicial (para t=0), t es el tiempo transcurrido y a es el factor por el que se Página Si 0<a<1 se trata de un decrecimiento exponencial. 1 multiplica en cada unidad de tiempo. UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL La función exponencial sirve para describir cualquier proceso que evolucione de modo que el aumento (o disminución) en un pequeño intervalo de tiempo sea proporcional a lo que había al comienzo del mismo. A continuación, se ven tres aplicaciones: • Crecimiento de poblaciones. • Interés del dinero acumulado. • Desintegración radioactiva. Esta función seria la protagonista para describir lo que ha sucedido con el crecimiento exponencial de pacientes en esta pandemia COVID 19. Si consideramos una función exponencial genérica: 𝑓(𝑥) = 𝑎 𝑥+𝑏 + 𝑐 La base ¨𝑎¨, nos indicara que tipo de gráfica vamos a obtener dependiendo de su valor: 𝒇(𝒙) = 𝒂𝒙+𝒃 + 𝒄 Si 𝟎 < 𝒂 < 𝟏 Si 𝒂 > 𝟏 Página Asíntota horizontal: 𝒚 = 𝒄 2 Como se mencionó anteriormente estas funciones presentan asíntotas horizontales, las mismas estarán definidas por el valor de ¨c¨: 𝑓(𝑥) = 𝑎 𝑥+𝑏 + 𝒄. Página 3 UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL Página 4 UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL Página 5 UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL Página 6 UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL Página 7 UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL Página 8 UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL Página 9 UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL Página 10 UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL UNCO- ANALISIS MATEMATICO I- FUNCION EXPONENCIAL ACTIVIDAD Represente gráficamente las siguientes funciones y determine dominio, imagen, asíntotas, intersección con ejes, máximo/ mínimo, intervalo de crecimiento y decrecimiento: 1. 𝑓(𝑥) = 2𝑥−2 − 6 2. 𝑓(𝑥) = 3𝑥 − 1 3. 𝑓(𝑥) = 2𝑥+4 − 2 4. 𝑓(𝑥) = 3𝑥+1 − 3 5. 𝑓(𝑥) = 2𝑥−2 + 1 6. 𝑓(𝑥) = 𝑒 𝑥+3 − 2 7. 𝑓(𝑥) = 𝑒 𝑥+1 + 3 +3 11 1 𝑥−2 9. 𝑓(𝑥) = (3) −1 Página 1 𝑥+3 8. 𝑓(𝑥) = (2)