UNIVERSIDAD TECNOLÓGICA DE PANAMÁ
CENTRO REGIONAL DE CHIRIQUÍ
FACULTAD DE INGENIERÍA DE SISTEMAS COMPUTACIONALES
DEPARTAMENTO DE COMPUTACIÓN Y SIMULACIÓN DE COMPUTADORAS
GUÍA DE LABORATORIO N°4
Facilitadora: Licda. Gabriela Caballero de Hislop, M.Sc.
Fecha: 31 – 10 – 2021
Estudiante(s): DILAN SOBENIS
Asignatura: Herramientas de Computación Gráfica
Grupo: 2IL131
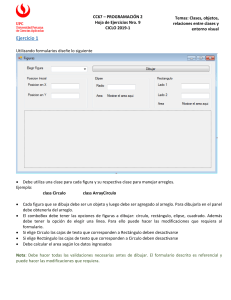
A. TÍTUL0 DE LA EXPERIENCIA: Algoritmos de discretización de primitivas geométricas
B. TEMAS: Esta es una asignación introductoria correspondiente al punto 2 del Módulo II del curso.
2. Algoritmos de discretización de primitivas geométricas.
2.1. Algoritmo DDA
2.2. Algoritmo de Bresenham
2.3. Algoritmo del punto medio para círculos
2.4. Algoritmo del punto medio para elipses
C. OBJETIVOS:
Objetivo General:
Implementar un algoritmo para la generación de círculos utilizando Visual C++ con OpenGL.
Objetivos Específicos:
Comprender los pasos que sigue el algoritmo del punto medio para la generación de círculos.
Crear un proyecto en Visual C++ que permita implementar el algoritmo del punto medio para la
generación de círculos con OpenGL.
D. METODOLOGÍA: La asignación es individual y se debe desarrollar durante la sesión de clases.
E. PROCEDIMIENTO O ENUNCIADO DE LA EXPERIENCIA:
Identifica los objetivos de la actividad.
Lee con atención las indicaciones en el documento que contiene el laboratorio a realizar.
Aplica el procedimiento demostrado en clases para crear proyectos Visual C++ con OpenGL.
Escribe tus observaciones sobre el desarrollo del Laboratorio al final de la rúbrica de evaluación,
detallando los logros, las dificultades y los aprendizajes.
Subir un archivo comprimido que contenga el proyecto puesto a punto y la Guía del Laboratorio. (Ver
rúbrica de evaluación del trabajo de laboratorio.)
F. RECURSOS:
Los estudiantes utilizarán los equipos computacionales disponibles en el laboratorio o en su defecto, los propios,
así como los recursos disponibles en la plataforma Moodle.
G. RESULTADOS: Es de esperar que cada estudiante:
Implemente un programa C++ con OpenGL, que cumpla con los requisitos del enunciado.
Guarde en una carpeta propia el programa creado, pues será utilizado como referencia en la tarea que
debe desarrollar aplicando el algoritmo estudiado en este laboratorio.
Complete la guía didáctica de actividad (apartado H) para esta asignación y la adjunte a los archivos
entregados.
H. CONSIDERACIONES FINALES: (Incluya en este apartado su opinión sobre el logro de los objetivos y el desarrollo de la asignación.
Cada estudiante/grupo debe subir esta guía, así como el documento escrito de su trabajo y la presentación )
Esta serie de laboratorios hasta ahora venía siendo algo complicado, sin duda, pero acá hay un punto de
inflexión donde debes pensar, probar y compilar tu algoritmo un buen par de veces para lograr el
objetivo del laboratorio. Entender el algoritmo no es lo complicado. Asignar – probar coordenadas lo es,
hacer comentarios para obviar algunas líneas y compilar también. Después de un buen tiempo lo
conseguí. Hay que destacar que una vez logras esta tarea, el algoritmo de elipse será mucho mas sencillo.
Muy buena asignación.
J. BIBLIOGRAFIA: (Pueden ampliar los recursos bibliográficos. Anótenlos en esta sección.)
1. Hearn, Donald y Pauline Baker. Gráficos por Computadora con OpenGL. Editorial Pearson/Prentice
Hall, 2006.
K. RÚBRICAS:
Evaluación:
Archivo del proyecto
Guía de la actividad completa
Total
40 puntos
10 puntos
50 puntos
Usaremos la rúbrica de evaluación presentada a continuación para evaluar la realización eficiente de este
Laboratorio.
RÚBRICA PARA EVALUAR TAREAS/LABORATORIOS PROGRAMADOS INDIVIDUALMENTE
PRESENTACIÓN
Criterios de
Evaluación
Excelente
4
1. Puntualidad
Entrega en la fecha
y hora señalada
2. Organización
En el programa se
identifican
adecuadamente los
procedimientos y se
describe su función
mediante
comentarios
3. Ortografía
Mantiene buena
ortografía.
Criterios de
Evaluación
1. Solución del
problema
(Eficiencia)
2. Estructura de
la solución
planteada
Bueno
3
Regular
2
Entrega en la
Entrega con un
fecha, pero no a
día de atraso.
la hora señalada
En el programa se En el programa se
identifican
identifican
adecuadamente
adecuadamente
la mayoría de los
la mayoría de los
procedimientos y
procedimientos y
se describe su
se describe su
función mediante función mediante
comentarios
comentarios
Presenta uno o
Presenta tres o
dos errores
cuatro errores
ortográficos.
ortográficos.
DESARROLLO
Deficiente
1
Ineficiente
0
Entrega con dos
días de atraso.
Entrega con tres
días de atraso.
En el programa
no se identifican
la mayoría de los
procedimientos y
no se describe su
función mediante
comentarios
El programa no
identifica los
procedimientos y
no describe su
función mediante
comentarios
Presenta cinco o
seis errores
ortográficos.
Presenta muchos
errores
ortográficos.
Excelente
Bueno
Regular
Deficiente
Ineficiente
La ejecución del
proyecto cumple al
100% con lo que se
solicita en el
enunciado.
20
El proyecto
muestra una muy
buena estructura
que permite la
legibilidad y
comprensión de
este.
8
La ejecución del
proyecto cumple
con 80% de lo
que se solicita en
el enunciado.
15
El proyecto posee
una buena
estructura,
aunque no facilita
mucho la
legibilidad y
comprensión de
este.
6
La ejecución del
proyecto cumple
con 60% de lo
que se solicita en
el enunciado.
10
El proyecto no
posee una buena
estructura, y no
facilita mucho la
legibilidad y
comprensión de
este.
La ejecución del
proyecto cumple
con 40% de lo
que se solicita en
el enunciado.
5
El proyecto no
posee una buena
estructura, lo que
dificulta la
legibilidad y
comprensión de
este.
4
2
La ejecución del
proyecto no
cumple con lo
que se solicita en
el enunciado.
0
El proyecto no
posee una
estructura
identificable, lo
que dificulta la
legibilidad y
comprensión de
este.
0
UNIVERSIDAD TECNOLÓGICA DE PANAMÁ
FACULTAD DE INGENIERÍA DE SISTEMAS COMPUTACIONALES
DEPARTAMENTO DE COMPUTACIÓN Y SIMULACIÓN
HERRAMIENTAS DE COMPUTACIÓN GRÁFICA
Laboratorio No. 4
Tema: Algoritmo del punto medio para la generación de círculos
Descripción de la actividad:
En este laboratorio deberá crear un programa con C++ y OpenGL. Utilice como base la estructura del
programa visto en el laboratorio anterior.
El objetivo es implementar el algoritmo del punto medio para la generación de círculos, por lo tanto,
asegúrese de que comprende las instrucciones de este. Es fundamental entender qué hace cada una de
las funciones del programa y de las líneas de instrucción que las conforman. Lea detenidamente los
comentarios que acompañan al segmento de código que corresponde al algoritmo y pregunte a la
docente si tiene dudas.
Algoritmo del punto medio para la generación de círculos:
Como en el algoritmo de líneas de Bresenham, el método del
punto medio calcula las posiciones de los píxeles a lo largo de la
circunferencia utilizando sumas y restas enteras, suponiendo
que los parámetros del círculo estén especificados en
coordenadas enteras de pantalla.
Como en cualquiera de los métodos de generación de círculos,
se reducen los cálculos considerando la simetría que los círculos
presentan. La forma del círculo es similar para cada uno de los
cuadrantes e inclusive, para cada uno de los octantes. Por lo
tanto, si se determinan las posiciones de la curva en el primer
cuadrante (que es el primer octante también) podemos generar simultáneamente cada una de las
secciones circulares de cada cuadrante.
El siguiente segmento de código ilustra los procedimientos que podrían emplearse para implementar el
algoritmo del punto medio para generación de círculos. Al procedimiento circleMidpoint hay que
pasarle el valor del radio del círculo y las coordenadas del centro del círculo. Entonces, se calcula una
posición de píxel dentro del primer octante de la trayectoria circular y se pasa dicha posición al
procedimiento circlePlotPoints. Este procedimiento almacena el color correspondiente al círculo en el
búfer de imagen para todas las posiciones simétricas dentro del círculo, efectuando llamadas repetidas
a las rutinas setPixel, que está implementada con las funciones de dibujo de puntos OpenGL.
/**************************
* Usaremos como referencia para este algoritmo el código que se incluye en las
* páginas 110-111 del libro de Hearn y Baker, cuya bibliografía aparece
* en el documento Guía de Laboratorio.
**************************/
class screenPt
{
private:
GLint x, y;
public:
/*Constructor predeterminado: inicializa las coordenadas a (0,0). */
screenPt( ) {
x = y = 0;
}
void setCoords (GLint xCoordValue, GLint yCoordValue) {
x = xCoordValue;
y = yCoordValue;
}
GLint getx ( ) const {
return x;
}
GLint gety ( ) const {
return y;
}
void incrementx ( ) {
x++;
}
void decrementy ( ) {
y--;
}
};
void setPixel (GLint xCoord, GLint yCoord)
{
glBegin (GL_POINTS);
glVertex2i (xCoord, yCoord);
glEnd ( );
}
void circleMidpoint (GLint xc, GLint yc, GLint radius)
{
screenPt circPt;
GLint p = 1 – radius; //Valor inicial para el parámetro de punto medio.
circPt.setCoords (0, radius); //Establece las coordenadas para punto superior del círculo.
void circlePlotPoints (GLint, GLint, screenPt);
/* Dibujar el punto inicial en cada cuadrante del círculo. */
circlePlotPoints (xc, yc, circPt);
/* Calcular el siguiente punto y dibujarlo en cada octante. */
while (circPt.getx ( ) < circPt.gety ( )) {
circPt.incrementx ( );
if (p < 0)
p += 2 * circPt.getx ( ) + 1;
else {
circPt.decrementy ( );
p += 2 * (circPt.getx ( ) – circPt.gety ( ))+ 1;
}
circlePlotPoints (xc, yc, circPt);
}
}
void circlePlotPoints (GLint
{
setPixel (xc + circPt.getx
setPixel (xc - circPt.getx
setPixel (xc + circPt.getx
setPixel (xc - circPt.getx
setPixel (xc + circPt.gety
setPixel (xc - circPt.gety
setPixel (xc + circPt.gety
setPixel (xc - circPt.gety
xc, GLint yc, screenPt circPt)
(
(
(
(
(
(
(
(
),
),
),
),
),
),
),
),
yc
yc
yc
yc
yc
yc
yc
yc
+
+
+
+
-
circPt.gety
circPt.gety
circPt.gety
circPt.gety
circPt.getx
circPt.getx
circPt.getx
circPt.getx
(
(
(
(
(
(
(
(
));
));
));
));
));
));
));
));
}
. . . . . . . .
Una vez puesto a punto el programa que genera el círculo, guárdelo. Haga una copia de ese programa y
modifíquelo para que genere la siguiente salida:
UNIVERSIDAD TECNOLÓGICA DE PANAMÁ
CENTRO REGIONAL DE CHIRIQUÍ
FACULTAD DE INGENIERÍA DE SISTEMAS COMPUTACIONALES
DEPARTAMENTO DE COMPUTACIÓN Y SIMULACIÓN DE COMPUTADORAS
CUADRO DE CALIFICACIÓN PARA EVALUAR TAREAS/LABORATORIOS DE PROGRAMACIÓN
GUÍA DEL ESTUDIANTE
TAREA/LABORATORIO No.: 4
TEMA: ALGORITMO DE PUNTO MEDIO PARA LA GENERACIÓN DE CIRCULOS.
Estudiantes: DILAN SOBENIS
Cédula: 4 – 810 – 1474
Criterios de evaluación de la actividad. (Puntos totales 40)
Presentación
Desarrollo
Elemento a Evaluar
Puntaje máximo
1. Puntualidad
4
2. Organización
4
3. Ortografía
4
1. Solución del problema
(Eficiencia)
2. Estructura de la solución
planteada
Entregó la guía de la Actividad completa
Puntaje obtenido
20
8
10
Total
Fecha: 31 – 10 – 2021
Observaciones del estudiante (detalle logros, dificultades y aprendizajes )
Este es uno de los laboratorios donde más he tardado en poder conseguir el resultado. Todo se basa en
numerosas pruebas de escritorio. Una vez que estructuré el programa e hice el primer llamado con los
3 parámetros de inicio, pude visualizar la circunferencia, pero luego tuve que tomar apuntes sobre que
hacia la función circlePlotPoint. Eso fue fácil, sin embargo, ahora aparecía una pregunta clave: ¿Como
dibujo todos esos trazos de circulo y llamo la función circlePlotPoint que debe tener diferentes setPixel
activos? No se si lo hice de la manera correcta o más eficiente, pero asigné una copia de esas dos
funciones (circulo, pot) con modificaciones en el nombre para cada trazo de circulo y luego las llamé con
unas coordenadas y unos colores diferentes para cada trazo.
#include<stdio.h>
#include<GL/glut.h>
#include<math.h>
void myinit(void)
{
glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, 640.0, 0.0, 480.0);
}
class screenPt
{
private:
GLint x, y;
public:
/*Constructor predeterminado: inicializa las coordenadas a (0,0). */
screenPt() {
x = y = 0;
}
void setCoords(GLint xCoordValue, GLint yCoordValue) {
x = xCoordValue;
y = yCoordValue;
}
GLint getx() const {
return x;
}
GLint gety() const {
return y;
}
void incrementx() {
x++;
}
void decrementy() {
y--;
}
};
void setPixel(GLint xCoord, GLint yCoord)
{
glBegin(GL_POINTS);
glVertex2i(xCoord, yCoord);
glEnd();
}
void circleMidpoint(GLint xc, GLint yc, GLint radius)
{
screenPt circPt;
GLint p = 1 - radius; //Valor inicial para el parámetro de punto medio.
circPt.setCoords(0, radius); //Establece las coordenadas para punto superior del círculo.
void circlePlotPoints(GLint, GLint, screenPt);
/* Dibujar el punto inicial en cada cuadrante del círculo. */
circlePlotPoints(xc, yc, circPt);
/* Calcular el siguiente punto y dibujarlo en cada octante. */
while (circPt.getx() < circPt.gety()) {
circPt.incrementx();
if (p < 0)
p += 2 * circPt.getx() + 1;
else {
circPt.decrementy();
p += 2 * (circPt.getx() - circPt.gety()) + 1;
}
circlePlotPoints(xc, yc, circPt);
}
}
void circlePlotPoints(GLint xc, GLint yc, screenPt circPt)
{
setPixel(xc + circPt.getx(), yc + circPt.gety());
setPixel(xc - circPt.getx(), yc + circPt.gety());
setPixel(xc + circPt.getx(), yc - circPt.gety());
setPixel(xc - circPt.getx(), yc - circPt.gety());
setPixel(xc + circPt.gety(), yc + circPt.getx());
setPixel(xc - circPt.gety(), yc + circPt.getx());
setPixel(xc + circPt.gety(), yc - circPt.getx());
setPixel(xc - circPt.gety(), yc - circPt.getx());
}
void dibuja(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0f, 0.1f, 0.0f);
circleMidpoint(150, 250, 100);
glFlush();
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitWindowSize(640, 480);
glutInitWindowPosition(0, 0);
glutCreateWindow("LINE DDA");
myinit();
glutDisplayFunc(dibuja);
glutMainLoop();
return 0;
}
El otro código, por lo extenso que es lo incluyo en un bloc de notas adjunto y acá solo muestro el
resultado que “conseguí”.