FugacidadMatiasKoppP.

See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/334284806
Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro
vapor – líquido en mezclas.
Preprint · July 2019
DOI: 10.13140/RG.2.2.16776.57601/1
CITATIONS
READS
0
17,991
1 author:
Matias Kopp Pailañir
Universidad de La Frontera
4 PUBLICATIONS 14 CITATIONS
SEE PROFILE
Some of the authors of this publication are also working on these related projects:
Solución a problemas en Ingeniería Química View project
All content following this page was uploaded by Matias Kopp Pailañir on 12 July 2019.
The user has requested enhancement of the downloaded file.
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
Fugacidad, Coeficiente de fugacidad y método
Gamma/Phi para el equilibro vapor – líquido en
mezclas.
M.Koppa
a
Departamento de Ingeniería Química. Universidad
de La Frontera. Francisco Salazar 01145, Temuco,
Chile.
Palabras claves: Fugacidad, Coeficiente de
fugacidad, Equilibrio vapor – liquido, Formulación
Gamma/Phi.
1. Resumen
La fugacidad como herramienta de trabajo logra
suplir las inexactitudes que se generan a partir del
cálculo de propiedades y la idealización de
sistemas termodinámicos. En ingeniería química
el equilibrio vapor – líquido (EVL) en mezclas
multicomponentes generan gran interés ya que
aportan información importante para el diseño de
equipos de separación y especialmente de
destilación. Este artículo tiene como finalidad
conocer el concepto de fugacidad, formular
ecuaciones para la determinación de esta
propiedad e introducir al concepto EVL a partir
de la formulación Gamma/Phi.
2. Introducción
La fugacidad es una medida del potencial
químico. Si consideramos un sistema bifásico de
una sustancia en condiciones de no equilibrio, la
pregunta que destaca y que otorga sentido físico
a la fugacidad es ¿en qué sentido la transferencia
de masa ocurrirá? Cuando las fugacidades de una
sustancia que está en contacto su fase líquida y
vapor son desiguales, la sustancia se
redistribuirá, con una transferencia de materia
neta desde la fase de mayor fugacidad a la de
menor fugacidad. Cuando las fugacidades son
iguales, la transferencia neta es cero y existe el
equilibrio (Murphy, 2015).
El equilibrio en termodinámica define un estado
de balance. En un estado de equilibrio no hay
potenciales
desbalanceados
(o
fuerzas
1
impulsoras) dentro del sistema, y éste no
experimenta cambios cuando es aislado de sus
alrededores (Çengel & Boles, 2009). Para hablar
de fugacidad debemos considerar el potencial
químico ya que ambos tienen una estrecha
relación tanto en el estudio EVL, como lo es en
la
teoría
de
soluciones.
Inicialmente
introduciremos el potencial químico de una
sustancia pura y, como caso concreto, el
potencial químico de un gas ideal. Su definición
fija las bases para la introducción del potencial
químico de una sustancia en una mezcla, que es
un concepto más general y potente (Atkins,
2006).
El estudio de EVL de mezclas a bajos puntos de
ebullición se aplican a muchos procesos
químicos como en industrias de petróleo y gas.
Recientemente, debido al papel de gases de
efecto invernadero el aumento de la temperatura
global a generado un creciente interés por
desarrollar tecnologías para la separación de
gases producto de la combustión. Por lo tanto, se
precisa la necesidad de modelos termodinámicos
EVL de mezclas como CH4 / CO2 para separar el
CO2 en la mezcla (Espanani et al., 2016). Por este
motivo el estudio de la fugacidad servirá como
inicio al complejo modelaje de soluciones.
Aplicando el concepto de fugacidad para los
componentes en mezcla, y utilizándolo
respectivamente para fase líquida y fase vapor, se
obtiene en el equilibrio una expresión que
relaciona ambas fases en términos de los
coeficientes Gamma para el líquido y Phi para el
vapor. Se presenta las bases para el cálculo de los
coeficientes de fugacidad en la fase vapor y se
desarrolla una expresión para evaluar las
condiciones del EVL (Salazar, 2011).
m.kopp01@ufromail.cl (M. Kopp.)
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
1
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
3. Potencial químico y equilibrio de fase
El potencial químico, µ, de una sustancia pura se
define como:
µ=#
𝜕𝐺
'
𝜕𝑛 (,*
(1)
El cambio en la energía de Gibbs total para el
sistema de dos fases es la suma de dichas
ecuaciones. Ya que el sistema de dos fases es
cerrado. La comparación de las ecuaciones
muestra que, en equilibrio:
9 µ2/ 𝑑𝑛/2 + 9 µ;/ 𝑑𝑛/; = 0
/
Es decir, el potencial químico muestra como
varia la energía de Gibbs de un sistema cuando se
añade una sustancia. Para una sustancia pura, la
energía de Gibbs es simplemente:
(5)
/
La conservación de la masa requiere que:
𝑑𝑛/2 = −𝑑𝑛/;
(6)
Por lo tanto:
𝜕(𝑛𝐺)
µ/ = #
' = 𝐺
𝜕𝑛/ (,*
(2)
9(µ2/ − µ;/ )𝑑𝑛/2 = 0
Para un sistema cerrado que consta de dos fases
en equilibrio, cada fase individual es un sistema
abierto con respecto a la otra, y es posible
producir transferencia de masa entre las mismas
(Demirel, 2014). Para cada fase es posible
escribir la ecuación:
𝑑𝐺 2 = 𝑉 2 𝑑𝑃 − 𝑆 2 𝑑𝑇 + 9 µ2/ 𝑑𝑛/2
(3)
/
𝑑𝐺 ; = 𝑉 ; 𝑑𝑃 − 𝑆 ; 𝑑𝑇 + 9 µ;/ 𝑑𝑛/;
(4)
/
Donde a y b identifican las fases. En este caso la
suposición es que el equilibrio implica
uniformidad en T y P en todas partes del sistema.
Las Ecs. (3) y (4) son las ecuaciones clave de la
termodinámica química. Esta ecuación se cumple
durante una reacción química irreversible y
durante el transporte de masa (Levine, 2004).
(7)
/
Esto solo se cumple para:
µ2/ = µ;/ (𝑖 = 1,2, … . , 𝑁)
(8)
En estos términos, fases múltiples con valores
iguales de T y P se hallan en equilibrio cuando el
potencial químico de cada especie es el mismo en
todas las fases.
“La materia fluye espontáneamente de una región
de alto potencial químico a una de menor
potencial químico. Otro nombre que suele darse
a el potencial es tendencia de escape. si el
potencial químico de un componente es alto, éste
tiene gran tendencia al escape” (Lewis, 1901).
4. Fugacidad de un gas
A partir de la Ec. (8), resulta claro que el
potencial químico proporciona el criterio para el
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
2
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
equilibrio de fases. No obstante, presenta
características que desalientan su uso. La energía
de Gibbs, y por lo tanto el potencial químico, se
definen con relación a la energía interna y
entropía. Por lo que se desconocen los valores
absolutos de la energía interna, también se
desconocen para el potencial químico. Por otra
parte, se conoce que el potencial químico se
aproxima hacia el infinito negativo cuando su
presión o composición se aproximan a cero
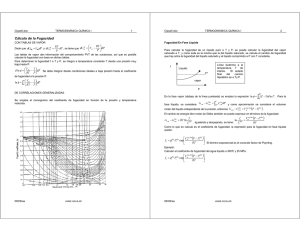
(Figura 1). Aunque esto no impide el uso de los
potenciales químicos, la aplicación del criterio de
equilibrio se facilita mediante la introducción de
fugacidad (Smith et al, 2007).
Para un gas ideal se tiene entonces:
G 𝑑𝐺 /H = 𝑅𝑇 G 𝑑𝑙𝑛 𝑃
(11)
Integrando se obtiene:
𝐺 /H = Ґ(𝑇) + 𝑅𝑇 𝑙𝑛 𝑃
(12)
Donde:
Ґ(𝑇): Constante de integración dependiente
exclusivamente de la temperatura.
La ley del gas ideal se puede usar para describir
el comportamiento de un gas real si la presión
mecánica es reemplazada por la presión efectiva
denominada fugacidad. esta al igual que el
potencial químico describe la tendencia al escape
de una sustancia (Lewis, 1901).
El origen del concepto de fugacidad reside en la
Ec. (12), la cual es válida solo para la especie
pura en estado de gas ideal. Para un fluido real se
escribe una ecuación análoga que defina ƒ como
la fugacidad de la especie.
Figura 1. Diagrama µ vs P.
/H
Consideremos desde un principio la ecuación
fundamental de Gibbs:
𝑑𝐺 = 𝑉𝑑𝑃 − 𝑆𝑑𝑇
(9)
Considerando un sistema a temperatura y
composición constante:
𝑑𝐺 = 𝑉𝑑𝑃
𝐺/ = Ґ/ (𝑇) + 𝑅𝑇 𝑙𝑛 𝑓/
(13)
La aproximación de la fugacidad a un gas real se
estima mediante propiedades residuales
termodinámicas donde, según definición para la
energía libre de Gibbs es G - Gig, donde el índice
ig representa un gas ideal (Smith, 2013; Kyle,
2015).
(10)
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
3
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
𝐺/M = 𝑅𝑇 𝑙𝑛
𝑓/
𝑃
variando los parámetros establecidos para cada
EOS (Lawal et al, 1993; Olivera, 1991).
(14)
Donde la relación adimensional ƒ/P se define
como el coeficiente de fugacidad, representado
por el símbolo Ø:
Ø/ =
𝑓/
𝑃
(15)
Donde β, q, I son factores para las diferentes EOS
a T y P determinadas y previamente calculadas
para componentes puros (Smith et al, 2007; Hu
et al, 2008).
A partir de la Ec (17) La ecuación virial truncada
al segundo término tiene el coeficiente B que es
función exclusiva de la temperatura. Así se puede
obtener una relación sencilla para la
determinación de la fugacidad:
Y que cumple con la siguiente definición:
ln Ø =
𝑓/
lim # ' = 1
*→S 𝑃
B(T): Constante dependiente de la temperatura
en la ecuación virial truncada al segundo término.
La determinación de los coeficientes de
fugacidad y por lo tanto de la fugacidad se
establece mediante distintos tipos ecuaciones
cúbicas de estados (EOS). En sus casos
especiales se le relaciona con la ecuación virial
donde se incluye el factor de compresibilidad y
una
ecuación
genérica
de
estado
respectivamente:
*
S
(19)
(16)
Es decir, a bajas presiones la fugacidad es la
misma que la presión (Ott & Boerio-Goates,
2000; Elliott, 1999).
ln Ø/ = G (𝑍/ − 1)
𝐵𝑃
𝑅𝑇
𝑑𝑃
𝑃
𝑇 𝑐𝑡𝑒
ln Ø/ = (𝑍/ − 1) − ln(𝑍/ − 𝛽/ ) − 𝑞/ 𝐼/
(17)
(18)
De esta forma para una EOS ya sea Ecuacion
virial, Van Der Waals, Redlich/Kwong,
Soave/Redlich/Kwong y de Peng/Robinson, se
puede calcular el coeficiente de fugacidad
5. Equilibrio vapor/liquido (EVL)
Un sistema aislado que consta de las fases en
contacto estrecho líquida y vapor, con el tiempo
alcanza un estado final en donde no existe
tendencia para que suceda un cambio dentro del
mismo. La temperatura, la presión las
composiciones de fase logran los valores finales
que en adelante permanecen fijos. El sistema se
halla en equilibrio (Kyle, 2015).
La Ec. (13) Que define la fugacidad nos indica
que es posible escribir esta relación en un vapor
saturado y en un líquido saturado a la misma
temperatura. De esta manera se establece que:
𝑓/] = 𝑓/^ = 𝑓/_2` = Ø/_2` 𝑃/_2`
(20)
“Para una especie pura, que coexiste en las fases
de líquido y de vapor están en equilibrio cuando
tienen la misma temperatura, presión y
fugacidad” (Smith et al, 2007).
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
4
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
la presión de vapor (Michelsen & Mollerup,
2004).
6. Fugacidad en líquidos
La fugacidad de un componente liquido puro es
aproximadamente idéntica a la fugacidad en la
fase vapor, a la presión de trabajo. Asumiendo
que el líquido es incompresible y al combinar las
ecuaciones, e integrando a temperatura constante
entre la presión de saturación y la presión del
sistema, obtenemos la relación (Minal, 2003):
𝑓b
𝑅𝑇 ln a b,c2` d = 𝑉 b (𝑃 − 𝑃 c2` )
𝑓
(21)
𝑉 b es el volumen molar del líquido puede
considerarse igual al volumen de líquido en
condiciones de saturación 𝑃 c2` , reemplazando:
f 𝐋,𝐒𝐚𝐭 = Ø𝐒𝐚𝐭 P 𝐒𝐚𝐭 se obtiene la ecuación para
poder obtener la fugacidad en la fase condensada.
𝑓 b = Øc2` 𝑃 c2` 𝑒
k l m*n* opq r
M(
(22)
La Ec. (20) Establece que en el equilibrio los
componentes de la fugacidad en el líquido y
vapor deben ser iguales, es importante poder
calcular los coeficientes mediante alguna EOS, la
cual otorgará el mismo valor tanto como para la
fase condensada como vapor. Esto se puede
demostrar calculando las fugacidades en la fase
vapor y liquida en un intervalo de temperaturas
menor a la crítica para una sustancia y graficando
nuestros resultados.
En la Figura 2. se puede apreciar que la
temperatura de equilibrio para el sistema esta
aproximadamente a los 27.2 °C, la fugacidad del
vapor muestra poca variación aproximadamente
a 1 mientras que en el líquido la no idealidad es
obvia. Por lo cual la fugacidad del líquido varia
fuertemente con la temperatura, al igual que con
Figura 2. Gráfico coeficiente de fugacidad vs
temperatura para propano a una presión de 10
bar.
7. Fugacidad en mezclas
El cálculo de la fugacidad en mezclas sigue el
mismo procedimiento conceptual que para
especies puras, pero con una notable diferencia:
Es necesario tomar en cuenta la influencia de la
composición. Este aspecto nos lleva a considerar
las reglas de mezclado para los parámetros de las
EOS. Si consideramos la Ec. (17) aplicada a una
solución debemos de escribir los términos
asociados a la composición de la respectiva
mezcla, por este motivo la ecuación virial
truncada al segundo término es exactamente la
misma que para un componente puro. Sin
embargo, ahora el parámetro B no solo es función
de la temperatura si no, también de la
composición. Esta fórmula puede ser demostrada
mediante mecánica estadística siguiendo las
reglas de mezclado aplicadas (Minal, 2003;
Smith et al, 2007; Lu et al., 2000):
𝐵s = 9 9 𝑦/ 𝑦u 𝐵/u
/
(23)
u
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
5
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
Donde yi designa la composición molar y Bm
caracteriza las interacciones biomoleculares. Se
puede relacionar los coeficientes viriales y la
fugacidad mediante la siguiente relación:
v/ =
ln Ø
𝑃 𝜕(𝑛𝐵)
w
x
𝑅𝑇 𝜕𝑛/ (,y
(24)
z
Y finalmente la expresión que se puede utilizar
es la siguiente:
v/ =
ln Ø
𝑃
{2 9 𝑦u 𝐵/u − 𝐵s |
𝑅𝑇
u
La ley de Raoult modificada incluye el
coeficiente de actividad para explicar las
desviaciones de la fase liquida, pero se encuentra
limitada por la suposición de la idealidad en la
fase vapor. esto último se supera introduciendo el
coeficiente de fugacidad de la fase vapor (Smith
et al, 2007). para la especie i en una mezcla de
vapor, la ecuación se escribe como:
(25)
]
v
𝑓•
~ = 𝑦/ Ø/ 𝑃
(27)
𝑓v~^ = 𝑥/ 𝛶/ 𝑓/
(28)
(,yz
Donde el coeficiente de fugacidad para la mezcla:
𝑓}
v/ = /
Ø
𝑦/ 𝑃
aproximaciones a los datos obtenido de
experimentos se implementa la formulación
Gamma/Phi.
Tomando las consideraciones de la Ec. (20)
v / 𝑃 = 𝑥/ 𝛶/ 𝑓/
𝑦/ Ø
(29)
(26)
Esta ecuación incluye los valores para las
especies puras Bii y Bjj también para Bij que
pueden ser calculadas para las especies puras
según alguna base de datos (McLaughlin &
Wisniak, 2014).
Donde:
v / : Coeficiente de fugacidad.
Ø
𝛶/ : Coeficiente de actividad.
𝑥/ : Fracción en la fase liquida.
𝑦/ : Fracción en la fase vapor.
8. Formulación Gamma/Phi y aplicaciones de la
fugacidad
Una vez revisado los conceptos teóricos de la
fugacidad y el cálculo de esta propiedad podemos
introducir a un método de aplicación utilizado en
la formulación real de sistemas en equilibrio
termodinámico. El EVL se estudia usualmente en
condiciones ideales, condiciones las cuales
entregan soluciones aproximadas a sistemas
complejos mediante ecuaciones de Raoult y
Henry a presiones moderadas. Así con la
necesidad
de
encontrar
las
mejores
Al reemplazar la Ec. (22) en la Ec. (29) por la
fugacidad y despreciando el factor de Poynting
(termino exponencial) y utilizando la relación:
𝛷/ =
v/
Ø
v _2`
Ø
/
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
6
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
Se obtiene deesta manera la formulación
Gamma/Phi para un sistema real esta dada por la
expresión:
𝑦/ 𝛷/ 𝑃 = 𝑥/ 𝛶/ 𝑃/_2`
(30)
soluciones. La regla de mezclado para la
ecuación Redlich-Kwong-Soave (RKS) es un
ejemplo:
𝑎s = 9 9 𝑥/ 𝑥u •𝑎/ 𝑎u (1 − 𝑘/u )
/
Ya llegados a este punto la aplicación sistemática
de estas ecuaciones depende de la disponibilidad
de correlaciones de la información a partir de las
cuales se pueden obtener valores para 𝑃/_2` , 𝛶/ ,
𝛷/ . La presión de vapor de una especie pura se
conoce de manera mas general por la ecuación de
Antoine. La forma de calcular el coeficiente de
actividad viene dada por diferentes métodos entre
los más conocidos está: Wilson, NRTL y el
método
UNIQUAC
(Minal,
2003;
Dadmohammadi, 2016).
A presiones moderadas en las que el
planteamiento Gamma/Phi es apropiado para el
EVL, los coeficientes de actividad se consideran
independientes de la presión. La necesidad de
iterar es evidente (Salazar, 2011). Por ejemplo,
un cálculo BUBL P (Calculo yi y P conocida xi y
T, requiere de valores para Φi, los cuales son a su
vez funciones de P y yi .En general para el cálculo
del punto de burbuja y roció se tienen las
siguientes ecuaciones respectivamente (Smith et
al, 2007; Elliott, 1999; Kyle, 2015):
𝑃 = ∑/
„… †… *…‡pq
ˆ…
(31) y 𝑃 = ∑
‰
‡pq
… Š… ˆ… /†… *…
(32)
Por lo tanto, se va a ilustrar como se obtiene la
curva de equilibrio vapor – líquido para una serie
de mezclas no ideales a partir de EOS, la
obtención del coeficiente de fugacidad y sus
respectivo gráfico.
(33)
u
𝑏s = 9 𝑥/ 𝑏/
(34)
/
Donde la fugacidad de la mezcla se calcula
mediante la ecuación:
∞
v r = G wa
𝑅𝑇𝑙𝑛mØ
𝑖
𝑉
𝜕𝑃 𝑅𝑇
− dx 𝑑𝑉 − 𝑅𝑇𝑙𝑛(𝑍𝑚 ) (35)
𝜕𝑛𝑖 𝑉
Para así obtener una ecuación similar a Ec. (18)
variando los parámetros β, q e I y considerando
las reglas de mezclado:
1
𝜕𝑛 𝑏
v r=
𝑙𝑛mØ
’ 𝑡 𝑚 “ (𝑍𝑚 − 1) − 𝑙𝑛m𝑍𝑚 − 𝑏𝑚 r +
𝑖
𝑏 𝑚 𝜕𝑛 𝑖
𝑍 +𝑐 𝑏
𝐴𝑚
1
𝜕𝑛 2 𝑎
1 𝜕𝑛 𝑏
# 𝑡 𝑚' − ’ 𝑡 𝑚 “— ln # 𝑚 2 𝑚'
–
2√2𝑏𝑚 𝑎𝑚 𝑛𝑡
𝜕𝑛 𝑖
𝑏 𝑚 𝜕𝑛 𝑖
𝑍𝑚 +𝑐1 𝑏𝑚
(36)
Esta fórmula (si bien modificada) es la utilizada
para determinar los coeficientes de fugacidad en
la mezcla, donde los parámetros fueron
estimados según las deducciones pertinentes. Se
calcularon los valores para el coeficiente de
actividad mediante el método NRTL y se procede
a realizar estimación del punto de roció y burbuja
mediante la iteración de las Ecs. (31) y (32) para
finalmente graficar los resultados obteniendo
para las curvas de equilibrio vapor – líquido a
diferentes temperaturas (Figura 5 – 8) (Espanani
et al., 2016).
Como podemos recordar el uso de una EOS
requiere una regla de mezclado usada para
obtener los parámetros para el cálculo de EVL en
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
7
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
Las Figuras 3 – 4 representan la metodología
iterativa para el calculo del punto burbuja según
los datos que sean conocidos (Salazar, 2011).
Figura 5. Curvas EVL Para CH4/CO2 a
diferentes temperaturas
Figura 3. Método iterativo para el calculo de el
punto burbuja a partir de una temperatura por la
aproximación Gamma-Phi.
Figura 4. Método iterativo para el calculo del
punto burbuja a partir de la presión por
aproximación Gamma-Phi.
Figura 6. Curva EVL para N2/CO2 con
diferentes reglas de mezclado
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
8
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
9. Conclusión
Figura 7. Grafico y1 vs x1 a diferentes
temperaturas
La fugacidad como concepto puede llegar a ser
una propiedad de difícil interpretación. Sin
embargo, se propuso simplificar el estudio y sus
expresiones otorgándole un sentido físico,
químico y matemático. comprendimos su
estrecha relación con el potencial químico y su
importancia no tan solo en la ingeniería química,
también en sistemas mas complejos como lo es el
medio ambiente. Por este motivo la realización
de aproximaciones a los datos reales fue un
desafío necesario para poder entender la
naturaleza de las cosas y encontrar soluciones a
problemas modernos como lo es la
contaminación ambiental mediante métodos más
complejos. De esta manera se abre puertas a la
estudio y compresión de sistemas reales EVL que
puede abordarse desde diferente aspecto,
considerando ambas fases como ideales o por el
contrario introducir coeficientes de fugacidad y
actividad si se consideran las fases no ideales. La
fugacidad en mezclas no ideales puede evaluarse
en termino de ecuaciones cúbicas de estado como
por ejemplo Van der Waals, para obtener
fugacidades en ambas fases. Pero para lograr
calcular estos valores se requiere de
procedimientos mucho mas elaborados desde un
aspecto de calculo matemático como es la
formulación Gamma – phi.
Queda a criterio del lector poder otorgarle uso a
esta información en diferentes tipos de
situaciones planteadas en las que se involucre
EVL sin sacrificar la inexactitud y aproximarse a
la realidad con el menor error posible.
Figura 8. Curvas EVL para N2/CO2 a
diferentes temperaturas
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
9
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
Referencias
Atkins, Peter; De Paula. (2006). Atkins' Physical
Chemistry. 8th edición., Oxford University
Press, Great Britain.
Çengel,
Y.A.
&
Boles,
M.A.
(2009). Termodinámica. 6ta Ed., McGraw-Hill,
México.
Dadmohammadi, Y., Gebreyohannes, S.,
Abudour, A. M., Neely, B. J., & Gasem, K. A. M.
(2016). Representation and Prediction of Vapor–
Liquid Equilibrium Using the Peng–Robinson
Equation of State and UNIQUAC Activity
Coefficient Model. Industrial & Engineering
Chemistry Research, 55(4), 1088–1101.
changing mixing rules of cubic equations of state.
Fluid Phase Equilibria, 95, 109–121.
Levine, I. N., Fisicoquímica, 5ª Edición, Vol I,
México, McGraw-Hill, 2004.
Lewis, G.N. (1901). The law of physicochemical change. Proceedings of the American
Academy of Arts and Sciences 37 (3): 49-69.; el
término "fugacidad" es introducido en p. 54
Lu, B.C.Y. & Peng, D.Y. (2000).
DISTILLATION | Vapour–Liquid Equilibrium:
Correlation and Prediction. Encyclopedia of
Separation Science, 1145–1159.
McLaughlin, E & Wisniak, J. (2014). Fugacity
and Fugacity Coefficient (Multicomponent).
Demirel, Y. (2014). Fundamentals of
Equilibrium Thermodynamics. Nonequilibrium
Thermodynamics, 1–74.
Michelsen, M.L. & Mollerup, J.M. (2004)
Thermodynamic models: fundamentals &
computational aspects. Tie-Line Publications,
Denmark.
Elliott, J.R. & Lira, C.T. (1999). Introductory
chemical engineering thermodynamics, Prentice
Hall PTR Upper Saddle River, NJ.
Minal, S. (2003). vapour-liquid equilibria and
infinite
dilution
activity
coefficient
measurements of systems involving diketones.
Espanani, R., Miller, A., & Jacoby, W. (2016).
Prediction of vapor–liquid equilibria for mixtures
of low boiling point compounds using Wong–
Sandler mixing rule and EOS/G E model.
Chemical Engineering Science, 152, 343–350.
Murphy, B.L (2015). Chemical Partitioning and
Transport in the Environment. Introduction to
Environmental Forensics, 167-197.
Hu, J., Wang, R., & Mao, S. (2008). Some useful
expressions for deriving component fugacity
coefficients from mixture fugacity coefficient.
Fluid Phase Equilibria, 268(1-2), 7–13.
Kyle, B.G. (2015). Chemical and Process
Thermodynamics 3a Ed., Pearson Education,
United States.
Lawal, A. S., & van der Laan, E. T. (1994). A
partial molar fugacity coefficient useful for
Olivera-Fuentes, C. (1991). Multicomponent
fugacity coefficients and residual properties from
pressure-explicit equations of state. Chemical
Engineering Science, 46(8), 2019–2029.
Ott, J. B., & Boerio-Goates, J. (2000). Summary
of Thermodynamic Relationships. Chemical
Thermodynamics: Advanced Applications, 1–42.
Salazar, F.G. (2011). Estimación del equilibrio
líquido vapor utilizando los coeficientes PhiGama.
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
10
Universidad de La Frontera
Facultad de Ingeniería y Ciencias
Departamento de Ingeniería Química
Smith, J., Van Ness, H. C., & Abbott, M. M.
(2007). Introducción a la termodinámica en
Ingeniería Química. 7a. ed., McGraw-Hill,
México.
Smith, R., Inomata, H., & Peters, C. (2013).
Underlying Thermodynamics and Practical
Expressions. Introduction to Supercritical Fluids
- A Spreadsheet-Based Approach, 275–332.
M. Kopp. Fugacidad, Coeficiente de fugacidad y método Gamma/Phi para el equilibro vapor – líquido
.
View publication stats
11