Departamento de Matemáticas y Estadísticas
ALGEBRA LINEAL
Trabajo Autónomo
UNIDAD # 2
El trabajo consiste en desarrollarlo en casa y luego subir el documento adjunto en PDF
las respuestas que se obtienen son en base a lo aprendido y desarrollado en el compendio,
clases asincrónicas, clases sincrónicas y recursos complementarios.
VECTORES EN Rn
1) Hallar el área de un triángulo formado por los vectores: 𝑢
⃗ = (3, −2,1) 𝑦 𝑣 =
(−2, −3,2)
2) Determine el volumen del paralelepípedo formado por los vectores: 𝑢
⃗ =
(−1, −1,1) ; 𝑣 = (−3, −3,4) 𝑦 𝑤
⃗⃗ = (0, −2, −4)
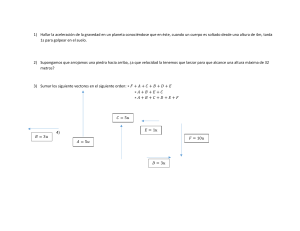
3) Sean
−2
𝑢 = ( 1 ),
−4
1
𝑢1 = (1),
1
1
𝑢2 = (0) ,
1
𝑦
1
𝑢3 = (1)
0
Entonces u es una combinación lineal de 𝑢1 , 𝑢2 , 𝑦 𝑢3 ya que la ecuación vectorial
(o sistema)
−2 = 𝑥 + 𝑦 + 𝑧
−2
1
1
1
( 1 ) = 𝑥 (1) + 𝑦 (0) + 𝑧 (1)
o
{ 1=𝑥+𝑧 }
−4 = 𝑥 + 𝑦
−4
1
1
0
a) Hallar x, y, z
b) Defina la combinación lineal: 𝑢 = 𝑥𝑢1 + 𝑦𝑢2 + 𝑧𝑢3
4) Sean 𝑢 = (4, −5, 5, −5), 𝑣 = (5, −5, 3, 2) y 𝑤 = (5, 4, 2,2). Demostrar que
pares de dichos vectores son ortogonales
5) Hallar el vector unitario de 𝑢
⃗ = (3, −2, √3)