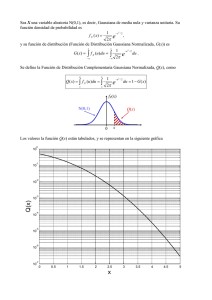
Física III Semestre de Otoño 2005 __________________________________________________________ 1 ESTUDIO DEL CAMPO ELECTRICO DE UN SISTEMA DE ESFERAS CONCÉNTRICAS CARGADAS, USANDO LA LEY DE GAUSS. a tiene una carga q 4 a 2 distribuida en su superficie, donde es la densidad superficial de carga. La región comprendida entre r a y r b se llena con una distribución volumétrica de carga con densidad radialmente uniforme, se decir, cte. El cascarón metálico comprendido entre r b y r c tiene una carga ( q ). Hallar el campo eléctrico y el potencial electrostático como La esfera metálica de radio función de r en todo el espacio. (Sugerencia: use la Ley de Gauss para el cálculo de los campos eléctricos) b c a q q r (r ) La ley de Gauss viene dada por: E dS Qneta encerrada 0 , donde Qneta encerrada significa la carga neta total encerrada dentro de la superficie gaussiana definida por nosotros mismos. Nótese que la toda la carga que pudiera haber fuera de la superficie gaussiana, no interviene para nada en el problema, porque su contribución al flujo eléctrico sobre la gaussiana es cero. En el caso de las esferas cargadas que estamos estudiando, la simetría del problema nos sugiere usar superficies gaussianas de forma esférica concéntricas con las esferas cargadas. En este caso, el campo eléctrico es siempre paralelo o anti paralelo a la diferencial de superficie en cada superficie gaussiana y por lo tanto, en este tipo de geometría siempre se cumple que E dS EdS , donde el signo más (menos) corresponde al caso en que E y dS _____________________________________________________________________ Profesores: Dr. Edmundo Lazo & Dr. Héctor Calisto Física III Semestre de Otoño 2005 __________________________________________________________ 2 son paralelos (antiparalelos). Adicionalmente sabemos que el módulo del campo eléctrico es constante sobre la superficie gaussiana de radio r fijo, ya que el campo sólo depende de su distancia al centro de simetría. Esto significa que en cada caso, la integral E dS E dS E 4 r 2 , donde S 4 r 2 es la superficie de la esfera gaussiana de radio r . Por otra parte, la carga neta encerrada en la gaussiana Qneta encerrada viene dada por r Qneta encerrada (r )dV , 0 donde (r ) es la densidad volumétrica de carga y donde dV 4 r 2 dr es el diferencial de volumen de la esfera. Nótese que el límite de integración superior llega sólo hasta la superficie gaussiana de radio r . La carga neta debe ser expresada en función del tipo de distribución de carga que nos dieron en el problema. Así, si la carga viene dada como densidad superficial (r ) , entonces r debemos escribir: Qneta encerrada (r )dS . 0 Comenzaremos aplicando la ley de Gauss a las esferas desde la de menor radio a la de mayor radio. I.- Cálculo del campo eléctrico usando Ley de Gauss. a) Caso r a . Con línea punteada se dibuja una superficie gaussiana de radio r a : Superficie gaussiana r a Dentro de esta gaussiana la carga neta es cero porque la carga q reside sólo en la superficie del conductor (en el caso estático, la carga en los metales siempre reside en sus superficies exteriores), luego 0 E dS , 0 relación que implica que: _____________________________________________________________________ Profesores: Dr. Edmundo Lazo & Dr. Héctor Calisto Física III Semestre de Otoño 2005 __________________________________________________________ E dS 0 3 E0 es decir, el campo eléctrico al interior de un conductor estático es siempre cero E 0. b) Caso a r b Con línea punteada se dibuja una superficie gaussiana de radio a r b Superficie gaussiana a r b b a q q r (r ) En este caso, la carga neta encerrada en la gaussiana es la suma de la carga q sobre la esfera metálica de radio a , más la fracción de carga contenida entre r a y el borde de la gaussiana r r , es decir, r b Qneta q dV , a dado que cte. , la carga neta encerrada vale Qneta q 4 (r 3 a 3 ) , 3 donde r es el radio de la esfera gaussiana y 4 (r 3 a 3 ) es el volumen del 3 cascarón esférico de radios a y r . Aplicando la ley de Gauss, tenemos Qneta 2 E dS EAesfera E 4 r 0 1 4 (r 3 a 3 ) E 4 r q 0 3 2 finalmente obtenemos: _____________________________________________________________________ Profesores: Dr. Edmundo Lazo & Dr. Héctor Calisto Física III Semestre de Otoño 2005 __________________________________________________________ 4 (r 3 a 3 ) q 4 . 3 4 0 r 2 Si r a , el campo eléctrico justo en la parte exterior de la superficie de la q esfera metálica de radio r a , vale E (r a ) . Este resultado es 2 0 4 0 a 1 E (r ) universal, es decir, en estado estático, justo en la parte exterior de un conductor de forma arbitraria con carga superficial , el módulo del campo eléctrico vale: . 0 Si r b , el campo eléctrico es producido por la contribución de la carga q en E la esfera metálica y de toda la carga contenida entre las superficies de radios r a y r b: E ( r b) (b 3 a 3 ) q 4 3 40 b 2 1 Antes de seguir, es muy importante calcular la carga total Q contenida entre las superficies de radios r a y r b : b Q 4 r 2 dr a 4 3 (b a 3 ) 3 c) Caso b r c Con línea punteada se dibuja una superficie gaussiana de radio b r c Superficie gaussiana b r c b c a r q (r ) q _____________________________________________________________________ Profesores: Dr. Edmundo Lazo & Dr. Héctor Calisto Física III Semestre de Otoño 2005 __________________________________________________________ 5 La aplicación de la ley de Gauss permite escribir E dS (q Q Qind ) 0 donde Qind es la carga inducida en la superficie interior del cascarón metálico de radios r b y r c . Sabemos que el campo eléctrico al interior de todo conductor es cero, E 0 , por lo tanto, la ecuación anterior queda: 0 (q Q Qind ) 0 , relación de la cual se desprende que Qind (q Q ) usando el resultado obtenido para q y para Q se escribe finalmente: 4 3 Qind q (b a 3 ) 3 Por conservación de la carga, esta misma carga inducida pero de signo contrario debe aparecer simultáneamente sobre la superficie exterior del cascarón metálico de radio r c , es decir, la carga total en r c debe ser Qc q Qind (q q Q ) Q . d) Caso r c Con línea punteada se dibuja una superficie gaussiana de radio r c Superficie gaussiana r c r q Q q La carga neta encerrada en esta gaussiana es la siguiente: Qneta q Q Qind Qc q Q (q Q ) Qc Qc pero, Qc Q , luego, Qneta Qc Q _____________________________________________________________________ Profesores: Dr. Edmundo Lazo & Dr. Héctor Calisto Física III Semestre de Otoño 2005 __________________________________________________________ 6 Al aplicar la ley de Gauss, podemos escribir: E dS E 4 r 2 Q 0 obteniendo finalmente E k Q r2 que tiene la forma del campo creado por una carga puntual Q . Este resultado es válido siempre, es decir, fuera de una esfera cargada, ya sea que se trate de una esfera de carga con distribución de carga con simetría esférica o un conductor metálico cargado, el campo eléctrico siempre tiene la forma k Qneta r2 donde Qneta es la carga total encerrada dentro de la esfera, no importa como E este distribuida, siempre que la distribución de carga tenga simetría esférica. En resumen, el campo eléctrico en función de r viene dado por: E (r ) 0 si E (r ) ra (r 3 a 3 ) q 4 si a r b 3 4 0 r 2 1 E (r ) 0 si b r c (b 3 a 3 ) E (r ) 3 0 r 2 si r c _____________________________________________________________________ Profesores: Dr. Edmundo Lazo & Dr. Héctor Calisto