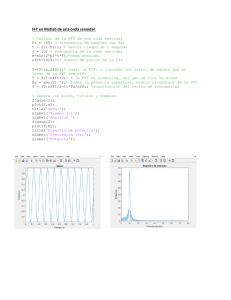
Resumen: En aplicaciones biomédicas integradas, los algoritmos de análisis de espectro, como la transformada rápida de Fourier (FFT), son cruciales para la detección de patrones y han sido el foco de una investigación continua. En sistemas profundamente integrados, como los marcapasos cardíacos, el procesamiento de señales basado en FFT generalmente se calcula mediante un circuito integrado específico de la aplicación (ASIC) para lograr un funcionamiento de baja potencia. Este informe propone un enfoque de diseño basado en datos para una solución FFT ASIC, que aprovecha el rango limitado de datos que encuentran estos sistemas integrados. Las optimizaciones propuestas en este resumen utilizan el concepto simple de hash y tabla de búsqueda para reducir efectivamente el número de operaciones aritméticas requeridas para realizar la FFT de una señal de electrocardiograma (ECG). Al reducir el consumo de energía dinámica y la huella energética general de la computación FFT, el diseño propuesto tiene como objetivo lograr una mayor duración de la batería de un marcapasos cardíaco. El diseño se sintetiza utilizando una biblioteca de células estándar de 90 nm y se simula la actividad de conmutación de nivel de puerta para obtener resultados precisos de consumo de energía. Las optimizaciones propuestas lograron un bajo consumo de energía de 27,72 nJ por FFT, que es un 14,22% más bajo que un FFT estándar de 128 puntos radix-2 cuando se probó con datos de ECG reales recopilados de PhysioNet. SECCIÓN I. Introducción La transformada de Fourier es sin duda uno de los algoritmos de procesamiento de señales más influyentes, particularmente para aplicaciones biomédicas [1] , [2] . Los avances del muestreo de señales digitales y la aparición de la transformada discreta de Fourier (DFT) permiten a los investigadores biomédicos analizar los componentes de frecuencia de las señales fisiológicas y detectar propiedades ocultas para identificar anomalías físicas. Tales métodos han sido particularmente efectivos para analizar señales fisiológicas como el electrocardiograma (ECG) [3] - [4] [5]. Una aplicación práctica del análisis de señales mencionado anteriormente se puede encontrar dentro de un marcapasos cardíaco implantable, que es un dispositivo encargado de la monitorización continua de las señales del ECG para detectar anomalías del ritmo cardíaco [6] . En caso de un ritmo intrínseco lento o falta de conducción normal del impulso, el marcapasos genera estimulaciones eléctricas para estimular el músculo cardíaco y mantener una frecuencia cardíaca adecuada. Un marcapasos tiene que funcionar en un entorno con una gran limitación de energía y puede durar un período muy largo (~ 7 a 10 años) con una sola batería [7] . Por lo tanto, el sistema integrado dentro de un marcapasos cardíaco necesita procesar la señal de ECG con la máxima eficiencia energética para garantizar una duración de batería suficientemente larga. Una arquitectura de sistema típica para un marcapasos cardíaco se muestra enFigura 1 . Figura 1. Diagrama del sistema integrado dentro de un marcapasos cardíaco. El coprocesador de señales resaltado en naranja es responsable del procesamiento continuo de los datos de ECG muestreados y es el objetivo de este informe. Ver todo Un procesador central supervisa el funcionamiento general, mientras que un coprocesador dedicado ejecuta el algoritmo de procesamiento de señales. El coprocesador de señales (resaltado en naranja en la Fig. 1 ) es responsable de calcular la transformada rápida de Fourier (FFT) o algoritmos de análisis de espectro similares [8] , [9] . Esto motiva el esfuerzo detrás de optimizar el diseño de un coprocesador FFT. Este informe presenta un método de cálculo FFT con eficiencia energética y su implementación VLSI que requiere un área de chip y hardware adicional mínima, pero logra una actividad de conmutación de circuitos y un consumo de energía dinámicos significativamente reducidos. SECCION II. Teoría y Motivación La FFT es un algoritmo eficiente para calcular la DFT y se prefiere en aplicaciones prácticas ya que tiene una complejidad de solo O ( N Iniciar sesión2norte ) [10] . Se calcula un par de muestras de señales de valor complejo utilizando una estructura de mariposa en el algoritmo FFT. En el hardware subyacente, cada mariposa realiza cuatro multiplicaciones y seis adiciones en el formato de representación numérico elegido. Los coeficientes reales e imaginarios de las variables complejas se pueden representar en representación de coma flotante, coma fija o coma flotante en bloque (BFP). Se prefiere el concepto de numeración BFP, donde se requiere precisión de cálculo y alto rango dinámico sin la complejidad añadida de implementaciones de punto flotante completo [11] . La representación BFP es atractiva para aplicaciones de procesador de señal digital (DSP), ya que puede proporcionar la precisión y el rango dinámico requeridos por algoritmos como FFT que utilizan aritmética de punto fijo [12]. A diferencia del punto flotante IEEE-754, el esquema BFP asigna un solo exponente a un conjunto de números. En esta disposición, se puede utilizar hardware de punto fijo para realizar operaciones aritméticas tales como multiplicación y suma en el bloque de mantisa. Después de cada operación, el exponente común asociado con el bloque debe escalarse para ajustarse al número más grande del conjunto de mantisas. A. Patrones de datos de ECG La detección y clasificación de anomalías en el ECG es clave para identificar varios tipos de latidos cardíacos anormales conocidos como arritmia. El proceso de clasificación requiere la extracción de ciertas características espectrales del ECG [17] , [18] . El proceso de extracción y clasificación de características basadas en FFT continúa durante todo el ciclo de vida operativo del marcapasos, consumiendo una parte significativa de la energía disponible. Por lo tanto, es muy deseable la optimización de la energía en el algoritmo FFT. Un ECG es un registro digital de los impulsos eléctricos del corazón capturados mediante electrodos sensores. La figura 2 muestra un registro de ECG digital de 11 bits trazado contra el tiempo. Los datos son casi periódicos con cada latido del corazón y muestran la conocida onda P, intervalo PR, complejo QRS, segmento ST, onda T y el período de reposo [15] . El análisis estadístico muestra que las muestras fuera del complejo QRS tienen un rango estrecho de valores (0 a 60) y una desviación estándar baja (18,3). Por lo tanto, dos muestras seleccionadas al azar fuera del complejo QRS tendrán una alta probabilidad de tener el mismo valor. Esto es válido para todos los ciclos de la señal de ECG en condiciones normales. Figura 2. Gráfico de muestras de ECG digitales de 11 bits de la base de datos de ECG a largo plazo del MIT-BIH [16] . Los marcadores indican varios segmentos de una señal de ECG. Excluyendo el complejo QRS, el rango de valores de señal está limitado entre 0 y 60. Ver todo Para este resumen, junto con una muestra de ECG normal, se recopilaron cuatro tipos de registros de ECG anormales de la base de datos de arritmias MIT-BIH [20] , [26] , que cubren los casos más comunes de arritmia. Los registros incluyen bradicardia sinusal (SBR), bloqueo AV (BAV), fibrilación auricular (AFIB) y aleteo auricular (AFL). La huella estadística de estos registros de ECG no ideales de 11 bits se resume en la Tabla I. SBR y AVB presentan una desviación estándar baja ya que el corazón no genera sus impulsos de estimulación natural en estas condiciones. Los valores de estas condiciones indican que en los casos más comunes de uso de marcapasos, los valores de muestra encontrados por el sistema tendrán una alta probabilidad de repetirse a lo largo del tiempo. Para los dos casos restantes de AFIB y AFL, la tasa de cambio es algo mayor debido a la naturaleza de las condiciones. Los valores calculados para la desviación estándar fueron 42,9 y 13,5 para AFIB y AFL, respectivamente. Aunque no se encuentra comúnmente, el análisis del rendimiento de la FFT propuesta durante el procesamiento de AFIB y AFL se suma a la robustez y escalabilidad del enfoque presentado en este resumen. TABLA I Estadísticas de los registros de ECG normales y anormales Debido a los valores repetidos observados, cuando una secuencia de entrada de cualquiera de estos registros de ECG se procesa a través de un algoritmo FFT, tiene lugar un número significativo de operaciones aritméticas redundantes. Para ilustrar la redundancia, se utilizaron muestras de todos los registros de ECG como entrada a un simulador BFP FFT de 128 puntos que utiliza el formato de datos Q15. En cada etapa de la FFT, se registraron los operandos para el paso de multiplicación dentro del cálculo de la mariposa. Se contó la aparición de combinaciones de operandos únicos y solo se tuvieron en cuenta las cinco combinaciones repetidas principales. Fig. 3muestra el porcentaje de multiplicaciones repetidas con respecto al total de multiplicaciones en cada etapa. Las cinco primeras entradas repetidas en las primeras cuatro etapas contribuyen al 38,3% de la multiplicación total en promedio. Al identificar las cinco multiplicaciones principales que ocurren en cada etapa y almacenar su resultado para futuras búsquedas, se evitará un número significativo de operaciones de multiplicación y conmutación de circuitos. Utilizando una tabla de búsqueda (LUT) relativamente pequeña de cinco entradas, este concepto de optimización se puede implementar para reducir el consumo de energía dinámica para una FFT de 128 puntos. El concepto de búsqueda de resultados en FFT ha sido posible en la implementación de software [18]basado en aritmética de punto flotante de precisión simple IEEE-754. Sin embargo, la utilización de esta técnica para BFP requiere una técnica de hash novedosa y amplía la efectividad a algoritmos FFT de conjuntos de muestras más grandes. Fig. 3. Gráfico de barras que muestra el porcentaje de multiplicaciones repetidas de las siete etapas en la FFT de 128 puntos provenientes de las cinco primeras entradas repetidas. Ver todo SECCIÓN III. Diseño propuesto El diseño del circuito integrado específico de la aplicación FFT (ASIC) se estructura en torno a una unidad de cálculo de mariposa. Un sumador con signo de 16 bits y un multiplicador con signo de 16 bits para el cálculo de BFP son los únicos bloques aritméticos en la unidad de cálculo de mariposa, controlada por una máquina de estados finitos. El diagrama del módulo de mariposa se muestra en la Fig.4. Como se indicó anteriormente, el multiplicador en la unidad de mariposa tiene acceso a una memoria de búsqueda de cinco entradas, que está diseñada para proporcionar los resultados de la multiplicación para los operandos más frecuentes. Realizar una búsqueda en la tabla requiere un algoritmo hash eficiente para generar un índice de búsqueda. En esta implementación, se utilizó una función hash XOR plegada para generar un índice para la LUT. La función hash XOR es popular por su simplicidad y excelente distribución no uniforme del valor hash para minimizar posibles conflictos [19] . Cada entrada al multiplicador se pasó a la función hash para generar un índice a la LUT. La función hash XOR calculó un valor hash de 4 bits haciendo XOR-ing los cuatro nibbles (4 bits) que existen en un número de 16 bits. El área requerida para sintetizar el multiplicador habilitado para búsqueda y la función hash fue5523 μ metro2 , simplemente un 9,7% más grande que el multiplicador de cabina estándar utilizado en un circuito FFT estándar. Figura 4. Diagrama de bloques de la unidad de mariposa. Una unidad de mariposa aritmética estándar BFP. Ver todo A. Arquitectura y rendimiento del sistema La arquitectura del FFT ASIC está diseñada alrededor del módulo de mariposa optimizado. Los principales componentes de soporte necesarios para el escalado de exponentes de BFP en cada etapa incluyen un cambiador con signo, un contador de exponente y un contador de bits iniciales. El módulo de cálculo de mariposa está diseñado para generar dos resultados complejosXI[ n ] y XI[ n + 1 ] y la variable máxima de 16 bits dentro XI[ n ] y XI[ n + 1 ] . La salida máxima de cada mariposa se almacena y se compara con los valores anteriores para encontrar la magnitud máxima generada en cada etapa de FFT. Antes del inicio de la siguiente etapa, el contador de bits principal usa esta magnitud máxima para encontrar el espacio libre que se puede usar para cambiar y escalar las variables de entrada a la siguiente etapa. El escalado mejora la precisión y permite un rango dinámico más alto en el proceso general. El valor de escala se usa para configurar la palanca de cambios para que cambie todos los datos leídos de los bancos de memoria. Con cada turno, el valor del contador de exponentes se actualiza de acuerdo con el valor de escala al final de cada etapa. La implementación se adhiere a la naturaleza "in situ" del algoritmo FFT, lo que significa que el resultado de cada etapa se volverá a escribir en la memoria para sobrescribir los datos originales. Los factores de giro necesarios para los cálculos se calculan previamente y se almacenan en dos módulos de memoria de solo lectura. La arquitectura general del sistema se da enFigura 5 . Figura 5. Diagrama de bloques simplificado de todo el coprocesador FFT. Basado en una sola unidad de mariposa, este circuito itera a través de la operación de mariposa de cada etapa secuencialmente. Ver todo Cada operación de mariposa requirió 12 ciclos de reloj para completarse. Además de la operación de mariposa, la lectura de datos de entrada, el escalado y la escritura en la memoria requirieron otros seis ciclos de reloj, lo que resultó en 18 ciclos de reloj en total. Para una FFT de 128 puntos, un total de64 × 7 = 448. se llevan a cabo operaciones de mariposas, lo que resulta en 448 × 18 = 8064. ciclos por FFT. La elección de una frecuencia de reloj máxima de 100 MHz permite que el cálculo se complete dentro de 8.064μ s , que es insignificante dentro de la ventana de acumulación de muestra. SECCION IV. Resultados y análisis Se implementaron dos diseños separados, con y sin la optimización propuesta, para la comparación. La síntesis y los diseños de los diseños se realizaron utilizando la biblioteca genérica Synopsys 90-nm [20] . Se habilitaron técnicas de bajo consumo como la sincronización del reloj y el uso de bibliotecas de vt mixtas. Se realizaron la simulación posterior a la ruta y la verificación de las reglas de diseño para garantizar la funcionalidad correcta antes de simular la lista de conexiones posterior a la ruta para estimar el consumo de energía. La actividad de conmutación durante la simulación se capturó en formato de intercambio de actividad de conmutación, que se utilizó junto con la información parasitaria utilizada en PrimeTime PX (PTPX) para determinar el consumo de energía basado en la actividad a un voltaje de funcionamiento de 1,2 V y una velocidad de reloj de 100,0 MHz. El desglose jerárquico del poder se muestra en la Tabla II.. La implementación del diseño optimizado fue posible dentro de un área de chips de 198404 μ metro2 (0,19 mm 2 ). TABLA II Desglose jerárquico del poder Para representar una carga de trabajo práctica, se utilizaron datos de ECG del mundo real para simular su funcionamiento. Se utilizaron como entradas cinco conjuntos diferentes de conjuntos de datos de ECG ideales y no ideales. El informe de análisis de potencia promedio fue informado por PTPX. El consumo de energía dinámico informado fue un 14,22% más bajo que el diseño FFT no optimizado. El tiempo requerido para terminar cada cálculo fue8,06 μ s , lo que arroja un consumo de energía promedio de 27,72 nJ para una sola FFT. El consumo de energía por FFT para diferentes conjuntos de entrada se muestra en la Fig.6 . Figura 6. Energía por FFT. El circuito FFT optimizado proporciona una solución de mayor eficiencia energética para procesar varias señales de ECG. Ver todo A. Comparación con el trabajo existente El enfoque de reducción de potencia de FFT presentado en este informe se compara con las soluciones de FFT de última generación de diferentes disciplinas y se muestra en la Tabla III . La energía de cada diseño se normaliza para eliminar el efecto de diferentes parámetros de diseño. Se utilizó una escala lineal utilizando la longitud de bits de datos, el tamaño de característica más pequeño, un número total de operaciones de mariposa y una escala exponencial del voltaje para escalar la energía por FFT de cada diseño. Los resultados normalizados destacan claramente los efectos beneficiosos de las optimizaciones frente a otros métodos de cálculo FFT. Aunque una FFT basada en eDRAM puede lograr resultados ligeramente mejores, lo hace con una mayor utilización del área y riesgo de falla de retención de memoria [23]. Ambas propiedades no son deseables en una aplicación de marcapasos compacta y crítica para la vida. TABLA III Comparación con las implementaciones de FFT de última generación B. Aplicación en dispositivos cardíacos Con un perfil de energía más pequeño, el nuevo FFT ASIC puede beneficiar a los dispositivos biomédicos implantables alimentados por batería para mantener un tiempo de ejecución más prolongado. En un marcapasos, la transformada de Fourier es uno de los cálculos principales que se ejecutan de forma continua en tiempo real. Por lo tanto, en tales aplicaciones, se espera que la reducción de energía extienda significativamente la vida útil de la batería. El sistema integrado en un marcapasos cardíaco normalmente alberga otros componentes del circuito, como un ADC, uno o más filtros analógicos, una bomba de carga para generar un voltaje más alto, un generador de pulsos para generar estimulaciones cardíacas y un DSP para calcular FFT y otras tareas de procesamiento de señales. [6] . Basado en la hoja de datos de un marcapasos moderno [7], un marcapasos normalmente consume un 67% de energía para el análisis de ECG y un 33% de energía para la estimulación durante la estimulación continua unicameral. Con base en estas distribuciones de energía y la energía FFT obtenida en este resumen, se calculan y se presentan en la Tabla IV la descomposición total de energía y la vida útil de la batería de un marcapasos . El tiempo de ejecución de la batería se calcula en función de una capacidad de batería de 3,36 Wh de [7] y una frecuencia típica de detección y operación de estimulación de 1 kHz [24]. La energía de cada operación de estimulación se utiliza para calcular el número absoluto de operaciones posibles hasta que la batería alcanza su estado de fin de servicio. Suponiendo que la detección y la estimulación continuas ocurren cada 1 ms (frecuencia de 1 kHz), se calculó que la duración de la batería para la FFT predeterminada es de 9,9 años. Los marcapasos disponibles comercialmente tienen una duración de la batería en el rango de 7 a 10 años, y varía con la gravedad del problema cardíaco y el requisito de estimulación correspondiente [7] , [25]. Usando el FFT ASIC presentado en este informe, el consumo de energía del algoritmo de detección se puede mejorar en un 14.22%, extendiendo el tiempo de ejecución general. Dado que la lógica de detección y las operaciones FFT están activas durante toda la vida útil del marcapasos, el ahorro de energía general se suma para ofrecer un tiempo de ejecución significativamente mejorado. TABLA IV Duración estimada de la batería de un marcapasos mediante el esquema de detección basado en FFT SECCIÓN V. Conclusión El procesamiento eficiente de datos biológicos, como las muestras de ECG, es una tarea desafiante en entornos con recursos limitados. Asegurar la eficiencia algorítmica y reducir el consumo de energía requiere optimizaciones específicas de la aplicación del hardware, junto con técnicas de implementación y síntesis de bajo consumo. Cuando se utiliza el conocimiento del dominio de los datos de ECG durante el desarrollo de la arquitectura del sistema, se hace posible una mayor comprensión y un diseño óptimo. En este resumen, se propuso y desarrolló una arquitectura FFT altamente eficiente analizando estadísticamente la naturaleza de FFT para calcular señales de ECG. Con base en los hallazgos, se propusieron modificaciones a la unidad de mariposa para desarrollar un ASIC FFT eficiente que minimice efectivamente su huella de energía. La reutilización de resultados aritméticos intermedios mediante el uso de LUT y operaciones BFP redujo la actividad de conmutación general y el consumo dinámico de energía en un 14,22% en varios casos de uso. La baja energía de cálculo de 27,72 nJ por 128 FFT directamente conducirá a una mayor duración de la batería en los marcapasos cardíacos en miniatura alimentados por batería.[26] del futuro. Aunque este enfoque novedoso para el cálculo de FFT se presentó para datos de ECG, el concepto de perfilar una señal y poblar las LUT apropiadas se puede aplicar a cualquier conjunto de datos que exhiba la probabilidad de muestras repetidas. Estas propiedades se observan en aplicaciones portátiles populares, como monitores de frecuencia cardíaca y rastreadores de actividad física. Otros algoritmos de procesamiento de señales estrechamente relacionados, como la transformada de Fourier de corta duración o la transformada de ondas discretas, también pueden beneficiarse de dicha optimización basada en la computación dinámica cuando se procesan señales con un rango de datos limitado y valores recurrentes. RECONOCIMIENTO El contenido es responsabilidad exclusiva de los autores y no necesariamente representa las opiniones oficiales de los Institutos Nacionales de Salud.