Galgas Extensiométricas: Guante para Control de Carro
Anuncio

Galgas Extensiométricas
1
2
3
𝐾𝑎𝑟𝑒𝑛 𝐹. 𝑉𝑖𝑙𝑙𝑎𝑟𝑟𝑎𝑔𝑎 𝐿𝑢𝑛𝑎 , 𝐾𝑒𝑣𝑖𝑛 𝐴. 𝐹𝑒𝑟𝑟𝑒𝑟 𝐶𝑜𝑟𝑟𝑒𝑎 , 𝑆𝑒𝑟𝑔𝑖𝑜 𝐴. 𝐻𝑢𝑟𝑡𝑎𝑑𝑜 𝑉𝑎𝑟𝑔𝑎𝑠
Facultad de Ciencias básicas e ingenierías
Universidad de los Llanos
Villavicencio, Colombia
1
karen.villarraga.luna@unillanos.edu.co
2
kevin.ferrer.correa@unillanos.edu.co
3
sergio.hurtado@unillanos.edu.co
Resumen— A continuación, se realiza el procedimiento para la
implementación de un guante, con galgas extensiométricas
adaptadas en cada dedo, donde según el cambio de resistencia
eléctrica es debido a la deformación aplicada, medido por las
galgas, se determina el movimiento de dos motores acoplados a
un carro casero y por ende, la forma en que éste se desplaza.
Las galgas se construyen con papel lija, lápiz y se protegen con
acetato; se realiza el procedimiento matemático de cada
circuito de acondicionamiento, donde se tiene en cuenta que el
circuito cumpla con la sensibilidad deseada. La programación
se realiza en Arduino y la comunicación por medio de
bluetooth.
Abstract—
Coming up next, the procedure for the
implementation of a glove is carried out, with strain gauges
adapted to each finger, where according to the change in
electrical resistance due to the applied deformation, measured
by the gauges, the movement of two motors coupled to a
homemade car and therefore, the way it moves. The gauges are
constructed with sandpaper, pencil and protected with acetate;
the mathematical procedure of each conditioning circuit is
carried out, where it is taken into account that the circuit
complies with the desired sensitivity. Programming is done on
Arduino and communication via bluetooth
I.
INTRODUCCIÓN
Las galgas extensométricas (strain gauges) son sensores
resistivos muy utilizados en la medida de esfuerzos
mecánicos en materiales en los que la resistencia efectiva
entre sus extremos se modifica con el esfuerzo aplicado
sobre la galga, es decir, estos sensores convierten la fuerza,
presión, tensión, peso, etc., en un cambio de la resistencia
eléctrica el cual puede ser medido.
Las aplicaciones de las galgas extensométricas pueden
clasificarse en dos grandes grupos: en primer lugar, las que
suponen la medida directa de un estado de deformación en
una superficie que permitirá conocer su estado tensional con
las restricciones ya establecidas; en segundo lugar, aquellas
en las que el estado de deformación es una variable
intermedia consecuencia de la variable que se pretende
medir. En este caso las galgas están configuradas de forma
que según su estado de deformación se conoce su estado
tensional, para luego utilizar ésta información según sea
necesario.
Como aspecto básico de todo dispositivo sensor tenemos el
circuito medida: para las galgas se usa siempre un circuito
en puente aunque se pueden incluir una, dos o -incluso-cuatro galgas activas con lo que se consigue aumentar la
sensibilidad del conjunto.
II.
OBJETIVOS
-
Realizar la aplicación del sensor resistivo, galga
extensiométrica, para la implementación de un
guante que permita controlar los movimientos de
los motores acoplados a un carro casero según la
deformación que se aplique a las galgas.
-
Comprender el principio de funcionamiento de las
galgas extensiométricas, para luego realizar la
correcta creación y aplicación de las galgas en el
circuito.
-
Acondicionar la señal de salida de las galgas como
sensor de tensión, de tal forma que la relación de la
deformación aplicada y la tensión de salida permita
determinar los movimientos finales mediante la
programación en arduino.
III.
MARCO TEÓRICO
A. Sistemas de medida.
Se denomina sistema a la combinación de dos o más
elementos, subconjuntos y partes necesarias para realizar
una o varias funciones. En los sistemas de medidas, esta
función es la asignación objetiva y empírica de un número a
una propiedad o cualidad de un objeto o evento, de tal forma
que lo describa. Es decir, el resultado de la medida debe ser:
independiente del observador (objetiva), basada en la
experimentación (empírica) y de tal forma que exista una
correspondencia entre las relaciones numéricas y las
relaciones entre las propiedades descritas. [1]
En la figura 1 se describe la estructura general de un sistema
de medida y control. En un sentido amplio, la realización de
una medida implica, pues, además de la adquisición de la
información, realizada por un elemento sensor o transductor,
también el procesamiento de dicha información y la
presentación de resultados, de forma que puedan ser
percibidos por nuestros sentidos.
C. Acondicionamiento y presentación.
Los acondicionadores de señal, adaptadores o
amplificadores, en sentido amplio, son los elementos del
sistema de medida que ofrecen, a partir de la señal de salida
de un sensor electrónico, una señal apta para ser presentada
o registrada o que simplemente permita un procesamiento
posterior mediante un equipo o instrumento estándar.
Consisten normalmente en circuitos electrónicos que
ofrecen, entre otras funciones, las siguientes: amplificación,
filtrada de impedancias y modulación o demodulación.
Si se considera, por ejemplo, el caso en que una de las
etapas de tratamiento de la señal de medida es digital, si la
salida del sensor es analógica, que es lo más frecuente, hará
falta un convertidor A/D. Éstos tienen una impedancia de
entrada limitada, exigen que la señal aplicada sea continua o
de frecuencia de variación lenta, y que su amplitud esté
entre unos límites determinados, que no suelen exceder de
10 V. Todas estas exigencias obligan a interponer un
acondicionador de señal entre el sensor, que muchas veces
ofrece señales que apenas unos milivoltios, y el convertidor
A/D.
La presentación de los resultados puede ser de forma
analógica (óptica, acústica o táctil) o numérica (óptica). El
registro puede ser magnético o sobre papel, e incluso
electrónico (memorias eléctricas), y exige siempre que la
información de entrada esté en forma eléctrica. [1]
Fig 1. Estructura general de un sistema de medida y control. [1]
Cualquiera de estas funciones puede ser local o remota,
implicando ello, en este segundo caso, la necesidad de
transmitir la información.
B. Tipos de sensores.
El número de sensores disponibles para las distintas
magnitudes físicas es tan elevado que no se puede proceder
racionalmente a su estudio sin clasificarlos previamente de
acuerdo con algún criterio.
Los sensores basados en la variación de la resistencia
eléctrica de un dispositivo son probablemente los más
abundantes. Ello se debe a que son muchas las magnitudes
físicas que afectan al valor de la resistencia eléctrica de un
material. Para la clasificación de los diversos sensores de
esta clase se toma como criterio el tipo de magnitud física
medida. [1]
Galgas extensiométricas
TABLE I
Clasificación de los sensores. [1]
Criterio
Clases
Ejemplos
Aporte de
energía
Moduladores
Generadores
Termistor
Termopar
Señal de salida
Analógicos
Digitales
Potenciómetros
Codificador de
posición
Modo de
operación
De deflexión
Acelerómetro de
deflexión
Servoacelerómetro
De comparación
D. Sensores resistivos
Las galgas extensométricas (strain gauges) son sensores
resistivos muy utilizados en la medida de esfuerzos
mecánicos en materiales en los que la resistencia efectiva
entre sus extremos se modifica con el esfuerzo aplicado
sobre la galga. [2]
Principio de funcionamiento
Supongamos un hilo de metal homogéneo de longitud l y
diámetro d sujeto entre dos puntos según se muestra en la
figura 2a.
Fig 2. Deformación de un sólido sometido a tracción: (a) situación original;
(b) modificación de la longitud y del diámetro con la fuerza de tracción
aplicada. [2]
La resistencia asociada al hilo de metal será proporcional a
su longitud e inversamente proporcional a su sección, es
decir:
𝑅 = ρ
∆ρ
ρ
=
+
∆𝑙
𝑙
𝑙
𝐾 =
2
−2
∆𝑑
𝑑
El cambio de longitud que resulta de aplicar una fuerza F a
una pieza unidimensional, siempre y cuando no se entre en
la zona de fluencia, viene dado por la ley de Hooke,
σ =
𝐹
𝐴
= 𝐸ε = 𝐸
𝑑𝑙
𝑙
donde E es la constante del material, denominada módulo de
Young, es la tensión mecánica y ε es la deformación
unitaria.
Si se considera ahora una pieza que además de la longitud l
tenga una dimensión transversal t, resulta que como
consecuencia de aplicar un esfuerzo longitudinal no sólo
cambia l sino que también lo hace t. La relación entre ambos
cambios viene dada por la ley de Poisson, de la forma
µ =
−
Dividiendo todos los términos de la expresión del cambio en
la resistencia efectiva del hilo por ∆𝐼/𝐼 y teniendo en cuenta
, se obtiene el denominado factor de galga, K
π𝑑
4
donde R es la resistencia del hilo y ρ, su resistividad.
Supongamos también que se aplica una fuerza F de tracción
a uno de los extremos con lo que el material se deformará
elásticamente (figura 2b). En principio, se modificarán las
dimensiones produciéndose un alargamiento del hilo y una
disminución de su sección que ocasionará un cambio en la
resistencia efectiva del hilo, cambio que quedará recogido
en la expresión:
∆𝑅
𝑅
Fig 3. Relación entre esfuerzos y deformaciones. La escala de la zona
elástica está muy ampliada. [1]
𝑑𝑡/𝑡
𝑑𝑙/𝑙
donde µ es el denominado cociente de Poisson y su valor
está entre 0 y 0,5.
∆𝑅/𝑅
∆𝐼/𝐼
= 1 + 2µ +
∆ρ/ρ
∆𝐼/𝐼
Este factor determina la sensibilidad de la resistencia a los
cambios en la longitud. Cuando sobre una galga se produce
una deformación por unidad de longitud de valor ∆𝐼/𝐼, el
cambio en la resistencia puede deberse a:
- El propio cambio de longitud.
- El cambio originado en la sección.
- El cambio originado en la resistividad.
Teniendo en cuenta la fuerza aplicada al hilo F, su sección
2
𝐴 = π𝑑 /4 y el módulo de Young del material E, se tiene
que las elongaciones por unidad de longitud ∆𝐼/𝐼 serán:
𝐹
𝐸𝐴
ε = ∆𝑙/𝑙 =
con lo que el cambio de resistencia resultará ser:
∆𝑅 =
𝐾𝑅
𝐸𝐴
𝐹
Así, la sensibilidad de la galga crece con el factor de galga y
el valor de la resistencia y decrece con el módulo de Young
y con la sección. Para lograr mayores cambios en ∆𝑅, será
conveniente incrementar el valor de la resistencia sin
incrementar la sección, es decir, tener mayores longitudes;
por otro lado, si lo que interesa es medir en una zona muy
concreta, el tamaño no puede ser muy grande con lo que se
impone una solución en la que el hilo se disponga en zig-zag
y se sitúe sobre una película que transmita lo mejor posible
el estado tensional al propio hilo.
Interesa que la galga mida esfuerzos en una sola dirección;
con la disposición de la figura 4b mide esfuerzos en el eje
vertical (y) mientras que los esfuerzos en el eje horizontal
(x) no debieran afectar porque la galga se pliega como un
acordeón. Sin embargo, en las zonas señaladas con círculos
en la figura 8b la dirección del cable coincide con la del
esfuerzo e introduce un error. Para reducirlo, se aumenta la
sección A en esta zona con lo que se reduce la sensibilidad
para el esfuerzo transversal en esos puntos.
En la figura 6 se presentan diversas aplicaciones relativas a
la medida de fuerza y par con elementos elásticos, en el caso
a se emplea un voladizo con una galga activa y, aparte, una
galga pasiva para compensación. En el caso b se emplean
dos galgas activas en el mismo voladizo, pero una de ellas
es transversal. En el caso c hay una célula de carga con tres
galgas activas en dirección longitudinal y otras tres en
dirección transversal. En el caso d se emplean cuatro galgas
activas, dos longitudinales y dos transversales. En el caso e
hay solo dos galgas activas; aparte hay dos gafas activas
para detectar esfuerzos de torsión, con sentidos opuestos dos
a dos. La medida de presiones, caudal, aceleraciones, etc., se
puede realizar con técnicas similares. [1]
Fig 4. Galgas extensiométricas de hilo: (a) construcción; (b) respuesta a la
fuerza. [2]
Tipos y aplicaciones
Los materiales empleados en la fabricación de galgas
extensiométricas son diversos conductores metálicos, como
las aleaciones constatan, advance, karma, isoelastic, y
también semiconductores como el silicio y el germanio. Las
galgas pueden tener o no tener soporte propio, erigiéndose
en su caso en función de la temperatura que se va a medir.
En la figura 5 se muestran diversos tipos de galgas
extensiométricas. Las galgas metálicas con soporte pueden
ser de hilo bobinado o plegado con soporte de papel, o
impresas o fotograbado. En este caso puede observarse en la
figura que se dispone de una gran variedad de
configuraciones, adaptadas a diversos tipos de esfuerzos.
Hay modelos para diafragma, para medir torsiones, para
determinar esfuerzos máximos y mínimos y sus direcciones
(rosetas múltiples), etc.
Fig 6. Diversas aplicaciones de las galgas extensiométricas a la medida de
magnitudes mecánicas. [1]
E. Medida de resistencias
A partir de variaciones de resistencia en respuesta a una
magnitud medida, se pueden obtener tensiones en un
margen útil para los convertidores analógicos-digitales o
para instrumentos de medida de magnitudes eléctricas.
El comportamiento general de un sensor basado en una
variación de resistencia z en respuesta a una variable a
medir, se puede expresar como 𝑅 = 𝑅0𝑓(𝑥) , con
Fig 5. Diversos tipos de galgas metálicas y semiconductoras, con y sin
soporte. [1]
𝑓(0) = 1. Para el caso en que la relación sea lineal se
tiene
𝑅 = 𝑅0(1 + 𝑥)
El margen de variación de x cambia mucho según el tipo de
sensor y, por supuesto, según el margen de variación de la
magnitud a medir. A efectos prácticos puede acotarse entre
a -1 para el caso de potenciómetros lineales de cursor
deslizante.
Cualquiera que sea el circuito de medida, hay dos
consideraciones con validez general para todos los sensores
resistivos. En primer lugar, todos ellos necesitan una
alimentación eléctrica para poder obtener una señal de
salida, pues la variación de resistencia en sí no genera señal
alguna. En segundo lugar, la magnitud de esta alimentación,
que influye directamente en la de la señal de salida, viene
limitada por el posible autocalentamiento del sensor, ya que
una variación de su temperatura influye también en su
resistencia.
Para la medida de resistencias se dispone de diversos
métodos, clasificados en métodos de deflexión y métodos de
comparación. En los primeros se mide la caída de tensión en
bornes de la resistencia a medir, o la corriente a su través, o
ambas cosas a la vez. Los segundos se basan en los puentes
de medida.
El método de deflexión más simple consiste en alimentar al
resistor con una fuente de tensión o corriente constante, y
medir la corriente a través del circuito o la caída de tensión
en el resistor, tal como se hace en los multímetros
analógicos y digitales, respectivamente. La aplicación de
esta técnica a los sensores resistivos viene limitada por el
hecho de que el valor máximo del cambio a medir puede ser
incluso de solo el 1%, y ello supone tener que medir
cambios de corriente o de tensión muy pequeños.
Otro método de deflexión es el de la doble lectura ( figura
7a). Consiste en disponer, en serie con el resistor
desconocido, uno de valor conocido y estable, y medir
sucesivamente la caída de tensión en este resistor y en el
desconocido, haciendo luego el cociente de ambas lecturas.
La primera lectura dará
𝑉𝑝 =
𝑉
𝑅𝑝+𝑅𝑥
𝑅𝑝
En la segunda lectura se obtendrá
𝑉𝑥 =
𝑉
𝑅𝑝+𝑅𝑥
𝑅𝑥
Si se dividen estas dos lecturas, se puede calcular 𝑅𝑥
mediante la relación
𝑅𝑥 = 𝑅𝑝
𝑉𝑥
𝑉𝑝
Si 𝑅𝑝 y 𝑅𝑥 tienen un valor similar, el error del voltímetro en
ambas medidas será prácticamente igual, cancelándose
parcialmente al hacer el cociente de las lecturas. La
utilización de un divisor de tensión es una técnica empleada
para medir resistores de valor elevado. Así, con referencia a
la la figura 7b, suponiendo que la resistencia de entrada del
voltímetro es mucho mayor que 𝑅𝑥, se tiene
𝑉𝑥 =
𝑉
𝑅𝑝+𝑅𝑥
𝑅𝑥
y de ahí se puede deducir el valor de la resistencia
desconocida,
𝑅𝑥 =
𝑉𝑥
𝑉−𝑉𝑥
𝑅𝑝
a)
b)
Fig 7. Acondicionamiento de la señal de un potenciómetro como sensor de
desplazamiento: a) esquema; b) circuito equivalente [1]
Dado que siempre es más fácil medir tensiones pequeñas
que tener una gran resolución en la medida de tensiones
grandes, el método empleado para medir cambios de
resistencia pequeños consiste en disponer otro divisor de
tensión en paralelo con aquel donde está incorporado el
sensor. Si se diseña además de forma que en reposo ambos
divisores den la misma tensión, basta medir la diferencia
entre las salidas de ambos para obtener una señal debida
solo al cambio en la variable medida. Esta estructura se
conoce como puente de Wheatstone. [1]
Mediciones con galgas extensiométricas
En la práctica, las mediciones con strain gauges raramente
involucran cantidades mayores que unos pocos milistrain
(mε). Por lo tanto, para medir esfuerzo se requiere de
máxima precisión sobre pequeños cambios de resistencia. El
factor de galga es la sensibilidad al esfuerzo de un strain
gauge. Supongamos que una pieza de prueba sufre un
esfuerzo de 500με. Una galga con un factor de galga de 2
mostrará un cambio en su resistencia eléctrica de
2*(500*10-6 ) = 0.1%. Para una galga de 120Ω, es un
cambio sólo de 0.12Ω. Para medir cambios tan pequeños de
resistencia y compensar la sensibilidad térmica, los strain
gauges son casi siempre utilizados en configuración puente
con excitación externa.
El circuito general de puente de Wheatstone, consiste en
cuatro brazos resistivos con una excitación de voltaje, Vex,
que se aplica a través del puente. El voltaje de salida del
puente, Vo, es igual a:
𝑅3
𝑉𝑜 = [ 𝑅 +𝑅 −
3
4
𝑅2
𝑅1+𝑅2
]𝑉𝐸𝑋
Fig 8. Puente de Wheatstone.[3]
De la ecuación anterior, cuando se da que R1 /R2 = R4 /R3,
el voltaje de salida Vo es nulo. Bajo estas condiciones, se
dice que el puente se encuentra balanceado.
Cualquier cambio de resistencia sobre cualquier brazo del
puente, resultará en una salida del voltaje no nula. Por lo
que si reemplazamos R4 con un strain gage activo, cualquier
cambio en la resistencia del strain gage causará el
desbalance del puente y producirá una salida no nula
proporcional al esfuerzo. [3]
F.
IV.
PROCEDIMIENTO
Para el desarrollo del laboratorio es necesaria la elaboración
de las galgas extensiométricas, las cuales son diseñadas en
papel lija número 1000 ya que este ofrece una buena
resistencia y flexibilidad, con un destornillador de pala
pequeño se raspa el camino sobre la lija y con un lápiz 6B se
rellenan estos caminos, que a su vez son cubiertas con papel
acetato para otorgar protección a los caminos de grafito
realizados, los cuales dan la resistencia característica de
cada galga dependiendo de qué tan grueso y grande sea este.
Haciendo uso de un multímetro se determina el valor de
resistencia aproximado de cada una y se tiene en cuenta que
estas sufrirán un desgaste a medida que se manipulan.
Para el montaje también se hace uso de potenciómetros de
valores entre 50k y 100k.
Lo siguiente a desarrollar se enfoca en la conexión entre el
sistema de motores, el módulo bluetooth y las galgas
extensiométricas, para tener más efectividad en el diseño del
circuito se usa la simulación de proteus donde se replica
cada una de las partes mencionadas (Figura 11).
El programa en arduino tiene como función leer la salida del
circuito
de
acondicionamiento
de
cada
galga
extensiométrica y de acuerdo a ese valor, el cual dependerá
de la elongación de la galga, se generan instrucciones
enviadas por medio de bluetooth al arduino que se conecta
al carro, es decir que al final el valor de resistencia en la
galga determina las órdenes.
Arduino
Arduino es una plataforma de electrónica "open-source"o de
código abierto cuyos principios son contar con software y
hardware fáciles de usar. Es decir, una forma sencilla de
realizar proyectos interactivos para cualquier persona. [4]
Básicamente lo que permite esta herramienta es la
generación de infinidad de tipos de microordenadores de
una sola placa, que luego pueden tener una amplia variedad
de usos según la necesidad de la persona que lo cree.
Se termina empleando para desarrollar elementos
autónomos, o bien conectarse a otros dispositivos o
interactuar con otros programas, para interactuar tanto con
el hardware como con el software, y este se puede clasificar
en dos tipos de uso:
1. Arduino es utilizado como un microcontrolador, cuando
tiene un programa descargado desde un ordenador y
funciona de forma independiente de éste, y controla y
alimenta determinados dispositivos y toma decisiones de
acuerdo al programa descargado e interactúa con el mundo
físico gracias a sensores y actuadores.
2. Arduino hace de interfaz entre un ordenador u otro
dispositivo, que ejecuta una determinada tarea, para traducir
dicha tarea en el mundo físico a una acción. Y viceversa,
gracias a sensores que están conectados a la placa Arduino
podemos hacer que el ordenador ejecute determinada
acción.
(a)
(b)
Fig 9. Código del guante en arduino
Con el fin de convertir la entrada dada en resistencia a una
señal de voltaje y con dicha señal determinar las
instrucciones que se envían, se tiene que hacer una
caracterización de las galgas.
Para dicha caracterización se toma en cuenta el rango de
variación de la resistencia cuando ésta está en reposo y
cuando se dobla sin llegar a fracturar el papel, así usando
una fuente de voltaje (suministrada por un arduino), se
obtiene una salida de variación del voltaje proporcional.
El circuito de acondicionamiento que se escogió es el
divisor de tensión, cuya resistencia conocida se determina
mediante potenciómetros de 50 kΩ y 100 kΩ.
Las entradas analógicas del arduino se caracterizan por leer
valores de tensión de 0 a 5 Voltios con una resolución de
1024 (10 bits). Si dividimos 5 entre 1024 tenemos que ser
capaz de detectar variaciones en el nivel de la señal de
entrada de casi 5 mV. Mediante la función
a=analogRead(A1) se almacena en a el valor leído, siendo
éste un valor que va de 0 a 1023 en proporción al nivel de la
señal de entrada. Para una entrada nula obtendremos el valor
0, para una entrada de 2.5 Voltios 511 (la mitad de 1023) y
para 5 Voltios 1023.
En el código de la figura 9a se leen los valores de tensión
ingresados por los pines A1, A2, A3, A4 y A5 del arduino y
mediante el comando BTserial.write(‘’) se envían por
bluetooht indicadores de la función que se ejecuta según
corresponda.
En la figura 9b se establecen los valores de tensión
correspondientes para entrar a cada instrucción, dándole
prioridad mediante la estructura del if{} a la instrucción
parar(), cuya lectura se realiza a la galga ubicada en el dedo
pulgar del guante, conectada a la entrada analógica A2 del
arduino. De manera similar, la del dedo índice determina la
instrucción adelante(), corazón atrás(), anular derecha() y
meñique izquierda().
Fig 10. Código del carro en arduino.
En el código de la figura 10, mediante el comando
dato=BTserial.read() se recibe por bluetooht la orden y se
guarda en la variable dato, para luego realizar la
comparación mediante if{}’s anidados y dirigirse a la
función que se indica desde el código del guante.
Así mismo, se dictan las direcciones en las que se mueven
los motores según la función. Arduino tiene pines de entrada
y de salida que pueden dar una pequeña cantidad de energía
que sirve por ejemplo para encender un LED, pero no
pueden alimentar a un motor. Para ello se necesita un
circuito que haga de intermediario. Este circuito toma
energía de otra fuente (corriente proveniente de un enchufe)
y siguiendo las instrucciones de Arduino hace funcionar el
motor. El básico que permite invertir el sentido de giro del
motor y graduar la velocidad de giro del motor es un puente
H.
Un motor DC cambia el sentido de giro cuando invertimos
los polos positivo y negativo en sus bornes, y este circuito
juega con una serie de interruptores para hacer ese cambio
de polaridad.
Entonces, por ejemplo, en la función adelante(), se
establecen los pines de salida A1 y B1 en LOW y A2 y B2
en HIGH; mientras que en la función atrás() A2 y B2
estarán en LOW y A1 y B1 en HIGH.
Fig 14. Conexiones del carro
En las figuras 12 a 14 se muestran los montajes finales del
carro casero y el guante con las galgas adaptadas.
Fig 11. Circuito implementado en Proteus
V.
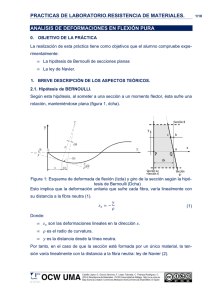
ANÁLISIS DE LOS RESULTADOS
Una galga extensiométrica es un sensor resistivo que varía
al aplicar una fuerza mecánica a ellas, la cual necesita un
circuito de acondicionamiento para obtener a su salida una
variación de voltaje.
Fig 12. Guante con las galgas indicadas
Fig 15. Acondicionamiento de señal de una galga extensiométrica por
divisor de tensión.
Para el acondicionamiento de las galgas extensiométricas, se
implementa un divisor de voltaje cuyo análisis del circuito
se plantea de la siguiente manera:
una galga extensiométrica, tiene una variación de resistencia
que se plantea como Ro (1+x) la cual está ubicada en serie
como se muestra en la figura 15, por lo que aplicando
divisor de voltaje, se tiene lo siguiente:
𝑉𝑠 =
𝑅2
𝑅1+𝑅2
𝑉𝑠(ε) =
𝑉𝑐𝑐 =
1+𝑘ε
2+𝑘ε
Fig 13. Conexiones de los divisores de tensión.
𝑉𝑐𝑐
señal de salida
𝑉𝑐𝑐
𝑉𝑠(0) =
𝑅0(1+𝑘ε)
𝑅0[1+(1+𝑘ε)]
𝑉𝑐𝑐
2
Donde:
k = factor de galga.
ε = deformación unitaria.
Vcc = entrada de alimentación
offset
La sensibilidad a la deformación está dada por:
𝑆=
𝑑𝑉𝑠
=
𝑑ε
𝑆 ≠ 𝑐𝑡𝑒,
𝑘
(2+𝑘ε)
2
𝑉𝑐𝑐
𝑘
4
𝑉𝑐𝑐
𝑆≈
Efecto de la temperatura 𝑅0𝑇 = 𝑓(𝑇)
𝑉𝑠 =
𝑅0𝑇(1+𝑘ε)
𝑅0+𝑅0𝑇(1+𝑘ε)
𝑉𝑐𝑐 (influye T)
Para el caso de un divisor con una galga ‘pasiva’ y una
galga ‘activa’, 𝑅1 = 𝑅0𝑇 y 𝑅2 = 𝑅0𝑇(1 + 𝑘ε)
𝑉𝑠(ε) =
𝑉𝑠 =
1+𝑘ε
2+𝑘ε
𝑉𝑐𝑐
(1+𝑘ε)
(2+𝑘ε)
señal de salida
Las galgas son indicadores de deformación capaces de
medir desplazamientos de hasta 土1 mm/m, son pequeñas,
livianas, flexibles de usar y tienen relativamente bajo costo,
estás características hacen que las sean la mejor opción para
la mayoría de los trabajos industriales a gran escala, y
también para las tareas más sencillas, sobre todo si se trata
de mediciones de alta precisión.
Un mayor desarrollo de las galgas extensométricas podría
hacer que se usasen en una mayor variedad de aplicaciones
que contribuirán al desarrollo industrial de los mercados
desarrollados y emergentes ya que por sus condiciones de
uso aún no son lo suficientemente eficientes y
recomendables en cuanto a durabilidad.
𝑉𝑐𝑐 (no influye T)
La ventaja del circuito de acondicionamiento en el que se
usa el divisor de tensión con una galga pasiva, se ve
reflejada en la temperatura, donde por medio de las
ecuaciones se observa que ésta no afecta el funcionamiento.
A la salida de estos dos circuitos se observa una sensibilidad
𝑘
no lineal, proporcional a 4 𝑉𝑐𝑐 y con offset diferente de
cero. Sin embargo, en este caso estas características de
salida no impiden el correcto funcionamiento del circuito,
debido a que en la programación solo se tiene en cuenta dos
valores aproximados de la resistencia: cuando la galga se
encuentra en estado de reposo, es decir, sin ninguna fuerza
aplicada, y cuando la galga se somete a una deformación
extrema propia del movimiento del dedo, sin llegar a
dañarla. Entonces al no ser necesario tener en cuenta
pequeñas variaciones de la resistencia según el movimiento,
y por ende del voltaje, algún error de linealidad y offset
serán despreciables.
Cuando la variación de la temperatura es significante o se
requiere de una exactitud mejor, se pueden emplear dos
galgas lo suficientemente cercanas como para estar
sometidas a los mismos cambios de temperatura, pero solo
una de ellas es sensible al esfuerzo o cambio de la variable
que debe ser medida.
VI.
Las galgas extensiométricas son los sensores que tal vez nos
proporcionan una sensibilidad mayor pero a la vez su vida
útil es muy corta, una manipulación brusca posiblemente
cause que sus valores iniciales cambien de una manera
abrupta y se pueda perder su funcionalidad.
CONCLUSIONES
La elección del sensor condiciona la sensibilidad, exactitud
y estabilidad de los instrumentos de medida. Al tener una
galgas extensiométricas en el circuito de acondicionamiento,
en este caso el divisor de tensión con una galga activa, se
tiene error debido al efecto de la temperatura.
Con el uso de una galga pasiva en lugar de la resistencia fija
se anula éste efecto a la salida, sin embargo, al ser galgas
artesanales se dificulta realizar todas del mismo valor
óhmico
VII.
REFERENCIAS
[1] R. Pallas Areny, “Sensores y acondicionadores de señal ” 4a ed,.
S.A. Marcombo, 2005, pp. 1, 4, 6-7, 19, 60-67, 99-104.
[2] M. A. Perez García, et al, “Instrumentación electrónica”,
Thomson, Madrid 2005, pp. 227-247
[3] J. Sosa, “Galgas Extensiométricas Strain Gages 1”
[4] Aquae Fundación, “¿Sabes qué es un Arduino y para qué sirve?”,
Paseo de la Castellana, 259C.